Understanding Basic Trigonometry Concepts
Trigonometry is the study of triangles and the relationship between their sides and angles, particularly in right triangles. This introduction covers the basic trigonometric functions such as sine, cosine, and tangent, explaining their ratios in relation to angles and sides. By understanding these fundamental concepts, you can apply trigonometry to solve various mathematical problems involving triangles.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Introduction to Trigonometry Basic Trigonometric Functions
What is Trigonometry? The study of triangles Relationship between sides and angles of a right triangle What is a right triangle? A triangle with a 90 angle 90
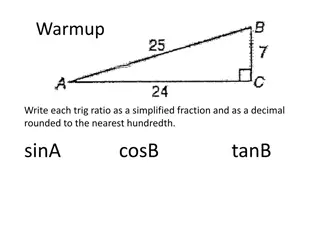
Review Right Triangles In relation to angle a, the sides of the triangle are: hypotenuse - always longest side and side across from right angle (90 ) adjacent - side closest to opposite - side opposite to a adjacent angle a angle a 90 opposite
Review Right Triangles Label the sides for angle b: hypotenuse adjacent opposite ? opposite ? 90 b ? adjacent
Trigonometric Functions Ratios of the sides in relation to angle a: sine cosine tangent a adjacent 90 opposite
Trigonometric Functions: SINE abbreviation: sin sin(a)= opposite hypotenuse a 0 sin 1 Example: sin(60 )= = ~.866 3 2 adjacent Ratio of opposite side to hypotenuse for 60 angle is 3 to 2 (.866 to 1) 90 opposite
Trigonometric Functions: COSINE abbreviation: cos adjacent hypotenuse cos(a)= a 0 cos 1 Example: cos(60 )= = .5 1 2 adjacent Ratio of adjacent side to hypotenuse for 60 angle is 1 to 2 (half) 90 opposite
Trigonometric Functions: TANGENT abbreviation: tan tan(a)= opposite adjacent adjacent opposite a 0 tan Example: tan(60 )= 3 = ~1.732 adjacent Ratio of opposite side to adjacent side for 60 angle is 3 to 1 (1.732 to 1) 90 opposite
Trigonometric Functions: REMEMBER: Opposite SOH CAH TOA SOH CAH TOA Sine = Hypotenuse a Adjacent Hypotenuse Cosine = adjacent Opposite Adjacent Tangent = 90 opposite
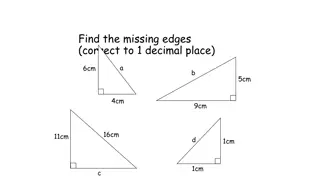
Using Trigonometric Functions: For any right triangle: calculate other sides if one side and angle known calculate angle if two sides known 90
Calculating Sides: One Side and Angle Known What is known? angle (50 ) and adjacent side (2) Solving for hypotenuse: Which function uses adjacent and hypotenuse? 50 2 COSINE 90 opposite
Calculating Sides: One Side and Angle Known What is known? angle (50 ) and adjacent side (2) Solving for hypotenuse: 50 2 ~0.643 cos(50 )= = hypotenuse 2 hypotenuse = ~3.111 90 opposite
Calculating Sides: One Side and Angle Known Now we know: angle (50 ) and hypotenuse (3.111) Solving for opposite: Which function uses opposite and hypotenuse? 50 2 SINE 90 opposite
Calculating Sides: One Side and Angle Known Now we know: angle (50 ) and hypotenuse (3.111) Solving for opposite: 50 opposite 3.111 ~.766 sin(50 )= = opposite = ~2.384 2 90 opposite 2.384
Calculating Angle: Two Sides Known What is known? adjacent (3) and opposite (5) Solving for angle (a): Which function uses adjacent and opposite? a 3 TANGENT 90 5
Calculating Angle: Two Sides Known What is known? adjacent (3) and opposite (5) Solving for angle (a): a 3 5 30.964 tan(a)= = .6 3 * need to use inverse tan tan-1(.6) = a = ~30.964 90 5