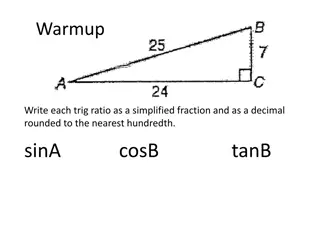
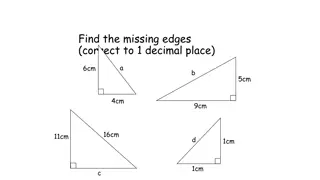
Trigonometry: Identities, Equations, and Problem Solving Techniques
Explore various trigonometric identities, solve trigonometry equations, and learn problem-solving techniques in trigonometry. Discover how to use basic trigonometry to find missing sides, understand trigonometric identities, and tackle challenging trigonometry problems involving sine, cosine, and tangent functions. Test your understanding with practical examples and learn strategies to solve trigonometry equations efficiently.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Challenge Questions ? ? ?
Trigonometric Identities
Trigonometric Identities ? ? ? ? ? ? ?
Trigonometric Identities Using basic trigonometry to find these two missing sides 1 sin? ? cos? ? ??? ? ??? ? 1 These two identities are all you will need for Further Maths. ? Then ??? ? = ????? + ????? = ? sin2? is a shorthand for sin?2. It does NOT mean the sin is being squared this does not make sense as sin is not a quantity that we can square! What do we get if we use Pythagoras Theorem? 2 ?
Solving Harder Trig Equations Solve sin? = 2cos? in the range 0 ? < 360 The problem here is that we have two different trig functions. Is there anything we could divide by to get just one trig function? 1. sin ? = sin 180 ? 2. cos ? = cos 360 ? 3. ???,??? repeat every 360 4. ??? repeats every 180 sin? cos?=2cos? ? cos? tan? = 2 ? sin ? cos ? ? = 63.43 ,243.43 ? A. tan? = B. sin2? + cos2? = 1 Tip: In general, when you have a mixture of sin and cos, divide everything by cos.
? ? ? ? ? ? ? ?
Test Your Understanding Solve 2s??? = cos? in the range 0 ? < 360 1. sin ? = sin 180 ? 2. cos ? = cos 360 ? 3. ???,??? repeat every 360 4. ??? repeats every 180 2tan? = 1 tan? =1 ? 2 ? = 26.57 ,206.57 sin ? cos ? A. tan? = B. sin2? + cos2? = 1 Solve cos? = sin? in the range 0 ? < 360 1 = tan? ? = 45 ,225 ?
Solving Harder Trig Equations June 2013 Paper 2 Q22 Solve tan2? + 3tan? = 0 in the range 0 ? < 360 This looks a bit like a quadratic. What would be our usual strategy to solve it? ? tan? tan? + 3 = 0 tan? = 0 ?? ? = 0,180, tan? = 3 108.43 ,288.4 ? ? 1. sin ? = sin 180 ? 2. cos ? = cos 360 ? 3. ???,??? repeat every 360 4. ??? repeats every 180 sin ? cos ? A. tan? = B. sin2? + cos2? = 1
More Examples Solve 2sin2? sin? = 0 in the range 0 ? < 360 sin? 2sin? 1 = 0 sin? = 0 ??sin? =1 ? 2 ? = 0,180 ,30 ,150 1. sin ? = sin 180 ? 2. cos ? = cos 360 ? 3. ???,??? repeat every 360 4. ??? repeats every 180 sin ? cos ? A. tan? = B. sin2? + cos2? = 1
More Examples Solve cos2? =1 4 in the range 0 ? < 360 cos? =1 2 ??cos? = 1 ? = 60 ,300 ,120 ,240 ? 2 1. sin ? = sin 180 ? 2. cos ? = cos 360 ? 3. ???,??? repeat every 360 4. ??? repeats every 180 sin ? cos ? A. tan? = B. sin2? + cos2? = 1
Test Your Understanding Solve cos2? + cos? = 0 in the range 0 ? < 360 cos? cos? + 1 = 0 cos? = 0 ?? cos? = 1 ? = 90 ,270 ,180 ? Expand and simplify (2? + 1)(? 1). Hence or otherwise, solve 2sin2? sin? 1 = 0 for 0 ? < 360 2sin? + 1 sin? 1 = 0 sin? = 1 2 ??sin? = 1 ? = 210 ,330 ,90 ?
Exercise 2 1 Solve the following in the range 0 ? < 360 ? ? a b sin? = 3cos? 2sin? = 3cos? ? = ??.?? ,???.?? ? = ??.?? ,???.?? Solve the following by first factorising. 0 ? < 360 cos2? cos? = 0 ? = ??,???,? tan2? 3tan? = 0 ? = ?,???,??.??,???.?? sin?cos? + sin? = 0 ? = ? ,??? 2 a b c ? ? ? Solve the following: 0 ? < 360 sin2? =3 4 cos2? =3 4 tan2? = 3 3 a ? = ?? ,??? ,??? ,??? ? b ? = ?? ,??? ,??? ,??? ? ? = ?? ,??? ,??? ,??? c ? By factorising these quadratics , solve in the range 0 ? < 360 3cos2? + 2cos? 1 = 0 ? = ??.?? ,??? ,???.?? 6sin2? sin? 1 = 0 ? = ?? ,??? ,???.?? ,???.?? sin?cos? + sin? + cos? = 1 ???? + ? ???? + ? = ? ? = ??? ,??? 4 a b ? ? ?
Proof Prove that 1 tan?sin?cos? cos2? ??? = 1 sin? Recall that means equivalent to , and just means the LHS is always equal to the RHS for all values of ?. cos?sin?cos? ? = 1 sin2????? = 1 sin2? = cos2? = ??? ? cos? ? ? 1. sin ? = sin 180 ? 2. cos ? = cos 360 ? 3. ???,??? repeat every 360 4. ??? repeats every 180 sin ? cos ? A. tan? = B. sin2? + cos2? = 1
Proof June 2012 Paper 1 Q16 1 1 Prove that tan? + tan ? sin ? cos ? ??? =sin? cos?+cos? Top Tip: Whenever you have a fraction in a proof question, always add the fractions. sin? ? sin2? sin?cos?+ cos2? sin?cos? ? = =sin2? + cos2? sin?cos? ? 1. sin ? = sin 180 ? 2. cos ? = cos 360 ? 3. ???,??? repeat every 360 4. ??? repeats every 180 1 = sin?cos?= ??? ? sin ? cos ? A. tan? = B. sin2? + cos2? = 1
Test Your Understanding Prove that tan ? cos ? 1 cos2? 1 sin? cos?cos? sin2? =sin? sin?= 1 ? = AQA Worksheet 1 Prove that tan2? cos2? 1 tan2? =sin2? cos2? 1. sin ? = sin 180 ? 2. cos ? = cos 360 ? 3. ???,??? repeat every 360 4. ??? repeats every 180 =1 cos2? cos2? ? cos2? cos2? 1 sin ? cos ? A. tan? = B. sin2? + cos2? = 1 = cos2?
Exercise 3 Simplify 3sin? sin? + 2 3 2sin? cos2? = ?????? + ????? ????? + ?????? = ? ????? + ????? = ? 1 ? 2 Write out the following in terms of sin?: a) cos2? tan2? = ?????????? ? ?????= ????? ??? ?????? = ????????? = ???? ? ????? c) cos? 2cos? 3tan? = ?????? ????? = ? ? ????? ????? ??? ? ? b) tan?cos3? = ? Prove the following: a. tan? 1 sin2? sin? 1 cos2? 1 sin2? tan2? c. 1 + sin? 1 sin? cos2? d. tan ? e. cos ? cos? sin?tan? f. 2sin? cos?2+ sin? + 2cos?2 5 3 b. 2 sin ? cos ? 2 2sin2? 1
Using triangles to change between Sine, Cosine and Tangent Given that sin? =3 acute, find the exact value of: a) cos? =? ? b) tan? =? ? ? 5 and that ? is ? 5 3 ? Represent as a triangle ? ? 4 Test Your Understanding 5 5 13 and that Given that tan? = ? is acute, find the value of: ? ? b) cos? =? ? ? 2 and that Given that cos? = ? is acute, find the value of: a) sin? =?? ?? b) tan? =?? ? ? 1 2 ? a) sin? = ?
