Understanding 3D Trigonometry Problems and Solutions

Exploring the challenges students face with 3D trigonometry, ways to assist them in grasping concepts, and studies linking spatial skills to math problem-solving abilities. An example of a glass roof lantern pyramid problem is presented, involving calculations of distances and angles based on given dimensions.

• Trigonometry
• Problem-solving
• Spatial skills
• Math education

berberich_s Follow

Uploaded on Sep 28, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

Presentation Transcript

1. van Hiele Example 3D Trigonometry

2. Leaving Certificate Syllabus

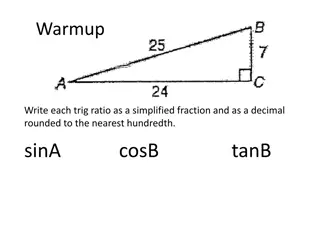
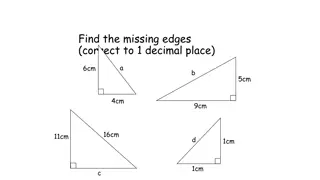
3. 3D Problems What do students find difficult about 3D trigonometry? How do you help students gain an understanding of 3D trigonometry? (The) study found a relationship between young children s construction skills and strong number sense and success in solving mathematical word problems (Nath & Sz cs, 2014) Children are as nonresponsive to short term explicit instruction on spatial transformation tasks as adults. (Ehrlich, Levine & Goldin-Meadow, 2006)

7. 1. Show that |AC|= 1.95m, correct to two decimal places. 2. The angle of elevation of B from C is 50 (i.e. | BCA| = 50 ). Show that |AB| = 2.3 m, correct to one decimal place. 3. Find |BC|, correct to the nearest metre. A glass Roof Lantern in the shape of a pyramid has a rectangular base CDEF and its apex is at B as shown. The vertical height of the pyramid is |AB|, where A is the point of intersection of the diagonals of the base as shown in the diagram. Also |CD| = 2.5m and |CF| = 3m

8. 1. Show that |AC|= 1.95m, correct to two decimal places. 2. The angle of elevation of B from C is 50 (i.e. | BCA| = 50 ). Show that |AB| = 2.3 m, correct to one decimal place. 3. Find |BC|, correct to the nearest metre. A glass Roof Lantern in the shape of a pyramid has a rectangular base CDEF and its apex is at B as shown. The vertical height of the pyramid is |AB|, where A is the point of intersection of the diagonals of the base as shown in the diagram. Also |CD| = 2.5m and |CF| = 3m