Trigonometry Practice Questions for Junior Certificate Ordinary Level
Practice solving trigonometry questions for the Junior Certificate Ordinary Level exam. Includes finding side lengths, calculating trigonometric ratios, and applying concepts such as Pythagoras' Theorem. Explore various scenarios involving right-angled triangles to enhance your understanding of trigonometry concepts.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Junior Certificate Ordinary Level Trigonometry www.mathsplus.ie www.mathsplus.ie www.mathsplus.ie
Junior Certificate Ordinary Level Question 1 Question 1 www.mathsplus.ie www.mathsplus.ie www.mathsplus.ie
(a) The right-angled triangle in the diagram has measurements as shown. Write down the length of the side opposite to angle A. (i) 12 12 Length of the side opposite to angle A = OPP HYP 12 (ii) Write down, as a fraction, the value of sin A. 15 ___ 15 =___ 5 4 A sin A = 9 opposite hypotenuse _________ sin =
(b) XYZ, In the right-angled triangle |XZ| = 13, | YXZ| = 60 . Using your calculator, write down the value of cos 60 . Z (i) cos 60 = 0 5 HYP 13 (ii) Using the diagram, complete the following |XY| cos 60 = adjacent hypotenuse 60 13 Y X ADJ (iii) Hence calculate |XY|. |XY| = 13 0 5 = 6 5
(c) As part of an activity lesson a group of students was asked to measure the height of the mast [RS]. The mast, [RS], is supported by the cable [RT]. R The students measured the distance from S to T and they also measured the angle STR. They found ST = 10 m and | STR| = 50 . OPP h 12 m 50 S T (i) Find the height of the mast RS. Give your answer correct to the nearest metre. 10 m ADJ opposite adjacent |RS| tan 50 = tan 50 = 10 |RS| = 1 1 917 2 m
(c) As part of an activity lesson a group of students was asked to measure the height of the mast [RS]. The mast, [RS], is supported by the cable [RT]. R c The students measured the distance from S to T and they also measured the angle STR. They found ST = 10 m and | STR| = 50 . Pythagoras Theorem 12 m 50 S T 10 m a2 + b2= c2 (ii) Using the theorem of Pythagoras, or otherwise, find the length of the supporting cable, RT . Give your answer correct to the nearest metre. c2= 102 +122 c2= c = 15 62 100 + 144 244 6 m
Junior Certificate Ordinary Level Question 2 Question 2 www.mathsplus.ie www.mathsplus.ie www.mathsplus.ie
(a) measurements (i) triangle. The diagram shows a right-angled triangle with as shown. Write down the length of the hypotenuse of the HYP 41 X 9 ADJ 40 adjacent hypotenuse 9 _________ =__ cos X = 41 (ii) Write down the value of cos X as a fraction.
C (b) In the right-angled triangle ABC, |AC| = 25 | BAC| = 32 . Let |BC| = x. 25 HYP x x = 25 0 53 = 13 25 OPP sin 32 = sin 32 = 0 5 299 3 opposite x = 32 hypotenuse 25 A B (i) Using your calculator find sin 32 . Write your answer correct to two decimal places. (ii) (iii) Using the diagram of the triangle ABC write sin 32 as a fraction. Hence, or otherwise, find x, the value of |CB| .
(c) Se n wishes to measure the width of a canal. He is at a point A directly opposite a landmark B on the opposite bank. Se n walks 50 paces along the bank of the canal to point C. He measures the angle ACB and finds it is 25 . Each of Se n s paces is 0 7 m. Calculate |AC| . Hence calculate the width of the canal, |AB| . Give your answer to the nearest metre. 35 m ADJ (i) (ii) C A 25 50 0 7 = 35 m opposite x 35 x = 35 tan 25 = 16 3207.. m adjacent tan 25 = OPP x B
Junior Certificate Ordinary Level Question 3 Question 3 www.mathsplus.ie www.mathsplus.ie www.mathsplus.ie
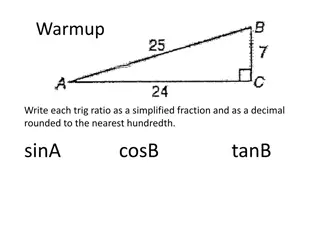
(a) shown. (i) The right-angled triangle ABC has measurements as Write down the length of the side opposite the angle C. Length of the side opposite to the angle C = 24 OPP 24 B C ADJ 10 26 C (ii) Write down the value of tan C, as a fraction. opposite adjacent A 24 _______ =___ 10 tan =
(b) In the right-angled triangle PQR, |PQ| = 14 and | PQR| = 53 . P Let |QR| = d. (i) (iii) Hence find d, the value of |QR|. Using the diagram write down the value of cos 53 , as a fraction. HYP 14 adjacent = 0 6 d hypotenuse 14 d = 14 0 6 = 8 4 cos 53 = cos 53 = 0 6018 . 53 Q R d ADJ (ii) Using your calculator, or otherwise, write down the value of cos 53 correct to one decimal place.
(c) [ZW] is a vertical television aerial mast. [ZX] and [ZY] are supporting cables. |ZX| = 15 m, |XW| = 12 m and |WY| = 16 m. Z Theorem of Pythagoras Hypotenuse (Side 1)2+ (Side 2)2= (Hypotenuse)2 15 m 9 m |ZW|2+ 122 =152 |ZW| + 2144 = 225 81 A X Y 12 m 16 m W |ZW| = 9 m (i) In XWZ, use the Theorem of Pythagoras, to find |ZW| , the height of the television aerial mast.
(c) [ZW] is a vertical television aerial mast. [ZX] and [ZY] are supporting cables. |ZX| = 15 m, |XW| = 12 m and |WY| = 16 m. A = tan 10 5625 = 29 3577 Z 15 m OPP 9 m A X Y 12 m 16 m ADJ W (ii) Hence find the measure of the angle marked A in the diagram correct to the nearest degree. opposite adjacent 9= 0 5625 =___ 16 _______ tan A =
Junior Certificate Ordinary Level Question 4 Question 4 www.mathsplus.ie www.mathsplus.ie www.mathsplus.ie
(a) shown. (i) The right-angled triangle ABC has measurements as Write down the length of the hypotenuse of the ABC. 17 C HYP 17 OPP 8 B A B 15 (ii) Write down the value of sin B, as a fraction. opposite hypotenuse 8 _________ =___ 17 sin =
P (b) In the right-angled triangle PQR, |QR| = 4, | QPR| = 48 and | PQR| = t . 48 (i) Find the value of t. t = 90 48 = 42 (ii) Using your calculator, or otherwise, write down the value of tan | PQR| correct to one decimal place. OPP tan | PQR| = tan 42 t 42 = 0 9004.. Q R 4 ADJ (iii) Hence, or otherwise, calculate |PR| correct to one decimal place. opposite tan 42 = 4 |PR| = 3 6 |PR| 0 9 = Multiply by 4 adjacent
(c) In the ABC, | BCA| = 90 , |AB| = 25 m and |BC| = 24 m. (i) Find, in metres, |AC|. B Pythagoras Theorem Pythagoras Theorem (Side 1)2+ (Side 2)2= (Hypotenuse)2 242+ |AC|2= 252 |AC|2= 625 576 + |AC|2= 25 m 24 m = 49 = 7 m = 7 m A C 7 m
(c) In the ABC, | BCA| = 90 , |AB| = 25 m and |BC| = 24 m. (ii) Find | BAC|, correct to the nearest degree. B opposite hypotenuse __________ sin | BAC| = 24 25 =___ HYP 25 m OPP | BAC| = 73 739 24 m = 74 A C 7 m
Junior Certificate Ordinary Level Question 5 Question 5
(a) shown. (i) The right-angled triangle ABC has measurements as Write down the length of the hypotenuse of the ABC. 10 Write down the value of cos C C HYP 10 6 (ii) C, ADJ as a fraction. cos =__________ A B 8 adjacent hypotenuse 6 =__ 5 =__ 10 3
P (b) PQR, In the right-angled triangle |PQ| = 8 and | PQR| = 50 . 40 (i) Find | QPR|. 8 | QPR| = 180 90 50 . = 40 50 R Q (ii) Using your calculator, or otherwise, write down the value of sin | QPR| correct to two decimal places. sin 40 = 0 64278 ..
P (b) PQR, In the right-angled triangle |PQ| = 8 and | PQR| = 50 . 40 (iii) Hence, or otherwise, calculate |QR| correct to one decimal place. HYP 8 5 opposite |QR| sin 40 = hypotenuse 8 From part (ii) Multiply both sides by 8 |QR| = 8 0 64 |QR| = 5 12 |QR| = 5 1 50 R Q OPP
(c) 5 m. In the ABC, | BCA| = 90 , |AB| =13 m and |AC| = B (i) Find, in metres, |BC|. Pythagoras Theorem (Side 1)2+ (Side 2)2= (Hypotenuse)2 52+ |BC|2= 132 |BC|2= 169 25 + |BC|2= 13 m 144 = 12 m A C 5 m
(c) = 5 m. In the ABC, | BCA| = 90 , |AB| =13 m and |AC| B (ii) Find | BAC|, correct to the nearest degree. adjacent hypotenuse sin =__________ HYP OPP 13 m 12 m 12 __ sin | BAC| = 13 | BAC| = 67 38.. A C 5 m ADJ
Junior Certificate Ordinary Level Question 6 Question 6 www.mathsplus.ie www.mathsplus.ie www.mathsplus.ie
(a) shown. (i) The right-angled triangle ABC has measurements as Write down the length of the side opposite the angle A. 24 24 A B OPP (ii) A, Write down the value of tan ADJ 7 25 as a fraction. opposite tan =_______ A C adjacent 24 7 =___
(b) PQR, In the right-angled triangle |PQ| = 12 and | QPR| = 60 . P (i) value Write down the 60 of cos 60 . 12 HYP ADJ cos 60 = 0 5 (ii) PR|. Calculate | R Q adjacent |PR| 0 5 = cos 60 = Cross multiply hypotenuse 12 |PR| = 6
(c) Claire is at a point c on the top of a cliff. The point B is at the base of the cliff. The height of the cliff is 35 m, as shown in the diagram. She wishes to find |BA|, the distance from the base of the cliff to the base of the lighthouse. She measured DCA and found it to be 41 . CD is parallel to BA. (i) Find | BAC|. C D 41 Alternate angles 35 m | BAC| = 41 41 A B
(c) Claire is at a point c on the top of a cliff. The point B is at the base of the cliff. The height of the cliff is 35 m, as shown in the diagram. She wishes to find |BA|, the distance from the base of the cliff to the base of the lighthouse. She measured DCA and found it to be 41 . CD is parallel to BA. (ii) Find, to the nearest metre, |BA|, the distance from the base of the cliff to the base of the lighthouse. C D opposite adjacent 35 41 tan 41 = tan 41 = 35 m OPP |BA| = 40 262 = 40 metres 41 A B 40 m ADJ
Junior Certificate Ordinary Level Question 7 Question 7
(a) shown. (i) The right-angled triangle ABC has measurements as Write down the length of the side adjacent to angle A. C 15 Length of the side adjacent to angle A = HYP 17 8 A A B 15 ADJ (ii) Write down the value of cos A, as a fraction. adjacent hypotenuse 15 =___ 17 _________ cos =
P (b) In the right-angled triangle PQR, |PQ| = 12, | PQR| = 37 . Let x = |PR|. Using the diagram, write down the value of sin 37 as a fraction. opposite sin 37 = 0 6 = (i) HYP x 12 hypotenuse 12 OPP x (ii) Using your calculator,write down the value of sin 37 correct to one decimal place. 37 sin 37 = 0 6018 . Q R (iii) Hence find x, the value of |PR|. x = 7 2
(c) Ciara wished to measure the width of a river. She was at A on the riverbank, directly opposite B on the other bank. Ciara walked from A to C, along the riverbank, at an average speed of 1 5 m/s. It took Ciara 30 seconds to reach C. She then measured ACB and found it to be 25 . B D S T 25 C A 45 m (i) by Ciara. Calculate |AC| , the distance walked Distance = Speed Time = 1 5 30 = 45 metres
(c) Ciara wished to measure the width of a river. She was at A on the riverbank, directly opposite B on the other bank. Ciara walked from A to C, along the riverbank, at an average speed of 1 5 m/s. It took Ciara 30 seconds to reach C. She then measured ACB and found it to be 25 . B OPP 25 C A 45 m ADJ (ii) the river. Hence, calculate |AB| , the width of Give your answer correct to the tan 25 = adjacent opposite |AB| tan 25 = nearest metre. 45 1 m |AB| = 20 983
Junior Certificate Ordinary Level Question 8 Question 8
(a) shown. (i) The right-angled triangle ABC has measurements as Write down the length of the side opposite the angle A. 5 C HYP 13 OPP 5 A B A 12 (ii) Write down the value of sin A, as a fraction. opposite hypotenuse 5 _________ =___ 13 sin =
(b) PQR, In the right-angled triangle P |PQ| = 10 and |PR| = 4. Find the value of cos PQR . (i) HYP 10 adjacent 4 = 0 4 hypotenuse 10 cos PQR = (ii) Hence find the measure of PQR, correct to the nearest degree. PQR = cos 10 4 Q R 4 = 66 421... ADJ = 66
(c) angle of 20 An aeroplane leaves the ground at an to the runway. Its speed is 28 m/sec. How far does the aeroplane travel in the first 30 seconds? (i) 840 m 20 Take-off point Distance = Speed Time = 28 30 D S T = 840 metres
(c) angle of 20 (ii) after the An aeroplane leaves the ground at an to the runway. Its speed is 28 m/sec. What is its height above the ground first 30 seconds? Write your answer to the nearest metre. HYP 840 m OPP h 20 Take-off point opposite h sin 20 = hypotenuse 840 h = 287 296.. metres
Junior Certificate Ordinary Level Question 9 Question 9
(a) shown. (i) The triangle abc has measurements as Write down the value of cos A. b adjacent hypotenuse 4 =__ _________ cos A = HYP 5 5 OPP 3 (ii) Write down the value of tan A. A a c 4 3 opposite adjacent =__ _______ ADJ tan A = 4
(b) A vertical building is 8 m high. It casts a shadow three times its height on horizontal ground. (i) Write down the length of the shadow. 3 8 = 24 m OPP 8 m B 24 m ADJ (ii) Find B, the angle of elevation of the sun, correct to the nearest degree. opposite tan B =8 adjacent 24 8 = 18 4349 24 B = tan 1
(c) A vertical flagpole [PQ], 12 m high, is supported by a cable [QR] as shown in the diagram. Q opposite hypotenuse _________ HYP 24 m sin A = OPP x 12 m 30 R P (i) Given that | QRP| = 30 , find the length of the cable [QR]. opposite 12 = 24 m sin 30 0 5 = hypotenuse x
(c) A vertical flagpole [PQ], 12 m high, is supported by a cable [QR] as shown in the diagram. Q Pythagoras Theorem HYP OPP 24 m a2 + b2= c2 12 m 30 R P y (ii) How far is R from P, the foot of the flagpole? Give your answer correct to one decimal place. y2+ 122 =242 y2+ 144 = 576 y2= 576 144 432 y = 20 784 8 m
