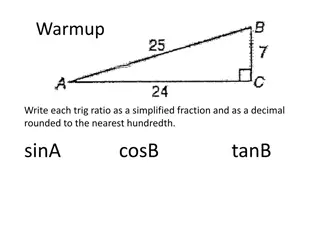
Understanding Moments and Trigonometry in Physics
Explore the concept of moments and trigonometry in physics through examples and problem-solving exercises. Learn how to calculate moments, find forces, and determine resultant moments using trigonometry. Enhance your understanding of the turning effects of forces and their applications in real-world scenarios.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Moments At angles
Moments: At an angle KUS objectives BAT solve problems using moments and friction at angles to a rod/ object using sohCahToa Starter: Spot the mistake
Moments The moment of a force measures the turning effect of the force on the body on which it is acting The moment of a force F about a point P is the product of the magnitude of the force and the perpendicular distance of the line of action of the force from the point P F P Moment of F about P = Fd clockwise d The magnitude of the force is measured in newtons (N) and the distance is measured in metres (m), so the moment of the force is measured in newton-metres (Nm) Moment of F about P = 15 Nm anticlockwise 3 m 5 N P
Using Trigonometry F You may need to use trigonometry to find the perpendicular distance sin d Nm sin Fd Moment of F about P = clockwise P d 10 N e.g. Moment of the force about P = = clockwise Nm 30 10 6 sin 30 30 P 6 m
WB 1 Calculate the moment about point A of each of these forces acting on a Lamina , ? 5 ? ? 40 6sin25 5sin40 6 ? 25 18 ? 10 ? ?????? = 10 5sin40 = 32.1 ?? ??? ?????? = 18 6sin25 = 45.6 ?? ??? 8 ? 70 ? 4sin65 ? 50 120 ? 65 ? 8cos50 4 ? ?????? = 70 4sin65 = 254 ?? ??? ?????? = 120 8cos50 = 617 ?? ??
WB 2 Given the moment about point A of each of these forces is 20 Nm, Find the magnitude of each force 3sin35 ? ? 5 ? 30 3 ? ?2 5sin30 35 20 ?2= 3sin35= 11.6 ? ?1 20 ?1= 5sin30 = 8 ? ?4 20 ?3 ?3= 2sin55= 12.2 ? 9sin75 ? 75 125 9 ? ? 2 ? 20 ?4= 9sin75= 2.30 ? 2sin55
WB 3a Two forces act on a lamina as shown. Calculate the resultant moment about the point A a) ?1= 8 10sin30 Moment of ?1 = 10sin30 8 = ?? ? 30 10 ? 50 Moment of ?2 = 10sin50 5 = ??? 10sin50 ?2= 5 Moment of ?1and ?2== ?? ?????????
WB 3b Two forces act on a lamina as shown. Calculate the resultant moment about the point A b) ?1= 12 70 Moment of ?1 = 10sin70 12 = 112.7 ??? 10 ? 10sin70 ? 8sin60 8 ? Moment of ?2 = 8sin60 15 = 103.9 ?? 60 ?2= 15 Moment of ?1and ?2= 112.7 103.9 = 8.8 ?? ?????????????
Moment on a uniform beam / rod WB4 review A light rod AB is 4 m long and can rotate in a vertical plane about fixed point C where AC = 1 m. A vertical force F of 8 N acts on the rod downwards. Find the moment of F about C when F acts a) at A b) at B c) at C a) Taking moments about C acw R 8 ?? = 8 ?? 1 m 3 m A C B b) Taking moments about C cw 8 ?? = 24 ?? 8 c) Taking moments about C cw 8 ?? = 0
WB 5 The diagram shows a set of forces acting on a uniform rod of mass 3 kg. Calculate the resultant moment about point A (including direction) 6cos45 6sin45 5cos70 5sin70 5 ? 6 ? 70 0.5? 45 4 ? 3 ? ? 0 3? Taking moments about A clockwise 5sin70 3 3? 0.5 = 11.8 ?? ????????? 6sin45 4 11.8 ?? ?????????????
WB6 50 to the horizontal by a force of magnitude F acting perpendicular to the rod at Q. Given that the rod has a length of 3 m and mass of 8 kg, find the value of F A uniform rod PQ is hinged at point P, and is held in equilibrium at an angle of ? ? 8? ? 50 Taking moments about P ? ? 3 = 8? 3 2cos50 8? 3 2cos 50 3 ? = = 25.2 ?
WB 7 A uniform rod PQ of mass 40 kg and length 10 m rests with the end P on rough horizontal ground. The rod rests against a smooth peg C where AC = 8 m The rod is in limiting equilibrium at an angle of 15 to the horizontal. Find a) The magnitude of the reaction at C b) The coefficient of friction between the rod and the ground ? 75 ? ? 40? a) Taking moments about P 15 ? ???????? distance 5cos15 ? 8 = 40? 5cos15 40? 5 cos 15 8 reaction at C ? = = 236.7 ? b) Equilibrium in horizontal direction ???????? = ?cos75 = 236.7cos75 = 61.25 Equilibrium in vertical direction ? + ???? 75 = 40? ? = 40? 236.7cos75 = 163.4 ? ? =?? ?=61.25 Coefficient friction 163.4= 0.375
WB 8 A ladder PQ of mass m kg and length 3a m rests with the end P on rough horizontal ground. The other end Q rests against a smooth vertical wall. A load of mass 2m is fixed on the ladder at point C, where AC = a. The ladder is modelled as a uniform rod in a vertical plane perpendicular to the wall and the load as a particle. The ladder rests in limiting equilibrium at an angle of 60 with the ground. Find the coefficient of friction between the rod and the ground N Add all the forces to the diagram ? Wall smooth No friction Equilibrium in horizontal direction 2? ???????? = ? ? R Equilibrium in vertical direction ? ? = 2?? + ?? = 3?? 60 ? Friction
WB 8 (cont)A ladder PQ of mass m kg and length 3a m rests with the end P on rough horizontal ground. The other end Q rests against a smooth vertical wall. A load of mass 2m is fixed on the ladder at point C, where AC = a. The ladder is modelled as a uniform rod in a vertical plane perpendicular to the wall and the load as a particle. The ladder rests in limiting equilibrium at an angle of 60 with the ground. Find the coefficient of friction between the rod and the ground N Taking moments about Q (to get an equation with Friction and R) ? Wall smooth No friction ? 3?cos60= ???????? 3?sin60 +?? 3 2? 2?cos60 + 2?? 2?cos60 Substituting ???????? ?? and R = 3?? ? R 3?? 3?cos60= ?3?? 3?sin60 +?? 3 ? 2?cos60 + 2?? 2?cos60 60 ? Friction Cancel by mga and rearrange to 7 2cos60 9sin60=7 3 3?? 3?cos60 +?? 3 2?cos60 2?? 2?cos60 3?? 3?sin60 = = 0.225 ? = 54
WB 9 (exam Q) A plank, AB, of mass M and length 2a, rests with its end A against a rough vertical wall. The plank is held in a horizontal position by a rope. One end of the rope is attached to the plank at B and the other end is attached to the wall at the point C, which is vertically above A. A small block of mass 3M is placed on the plank at the point P, where AP = x The plank is in equilibrium in a vertical plane which is perpendicular to the wall The angle between the rope and the plank is , where tan =3 The plank is modelled as a uniform rod, the block is modelled as a particle and the rope is modelled as a light inextensible string 4 a) Using the model, show that the tension in the rope is 5?? 3?+? 6? sin? =3 cos? =4 5 5 3 ? T Friction 4 5 R Mg 3Mg
WB 9a (exam Q cont ) a) Using the model, show that the tension in the rope is 5?? 3?+? 6? a) Taking moments about A ?sin 2? = ?? ? + 3?? ? ???? ?sin Friction R Rearranges to ? 6? 5= ?? ? + 3?? ? a Mg 3Mg Rearranges to 5 6? ??? + 3??? =5?? ? + 3? ? = QED 6?
WB 9b (exam Q cont ) The magnitude of the horizontal component of the force exerted on the plank at A by the wall is 2Mg Find x in terms of a b) Horizontally forces are in equilibrium 2?? = ???? ???? ?sin Friction Substituting result from a) gives R=2Mg 2?? =5?? ? + 3? a ??? 6? Mg 3Mg 2?? =5?? ? + 3? 4 6? 5 ?+3? 3? Cancel by 2Mg to simplify gives 1 = then to ? =2 Rearranges to a + 3? = 3? 3?
WB 9c (exam Q cont ) The force exerted on the plank at A by the wall acts in a direction which makes an angle with the horizontal c) Find the value of tan? c) Resolve forces vertically ???????? + ???? = 4?? ???? ?sin Friction ???????? +5?? ? + 3? 3 5= 4?? R=2Mg 6? Rearranges using ? =2 3? a ???????? = 4?? ?? ? + 2? =5 Mg 3Mg 2Mg 2? Now find tan 52Mg 2?? Friction =5 2Mg =5 tan? = 4 ? R=2Mg
WB 9d (exam Q cont ) The rope will break if the tension in it exceeds 5 Mg d) Explain how this will restrict the possible positions of P. You must justify your answer carefully previous results: ? =5?? ?+3? 6? ???? ?sin Friction=2 5?? we know: ? =5?? ?+3? 5?? 6? R=2Mg a simplify by cancelling and rearrange 5 ?+3? 6? 5a + 15x 30? Mg 3Mg 5 So the distance AP must be less than 5 For the rope NOT to break 3? ? 5 3?
KUS objectives BAT solve problems using moments and friction at angles to a rod/ object using sohCahToa self-assess One thing learned is One thing to improve is