Trigonometry Essentials: Missing Edges, Angle Calculations & Triangle Identification

Slide Note

Explore a comprehensive guide on trigonometry covering calculating missing lengths, determining angles, labeling sides of triangles, and solving problems using trigonometry. Learn about hypotenuse, opposite side, adjacent side, and practical applications through examples and visual aids.

jazmin Follow

Uploaded on Jul 14, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

E N D

Presentation Transcript

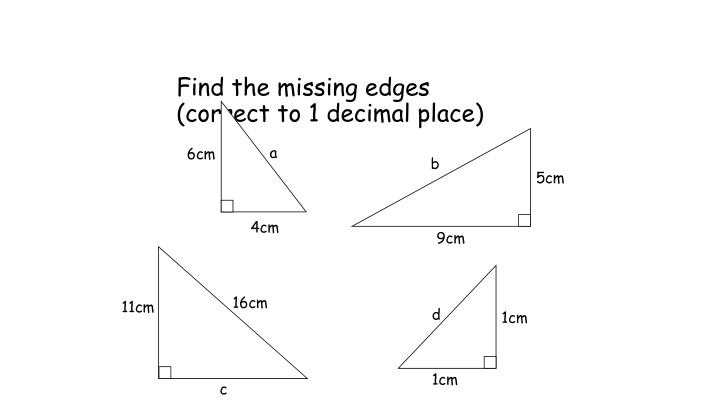
Find the missing edges (correct to 1 decimal place) a 6cm b 5cm 4cm 9cm 16cm 11cm d 1cm 1cm c

Answers 7.2cm 6cm 10.3cm 5cm 4cm 9cm 16cm 11cm 1.4cm 1cm 1cm 11.6cm

We can label the sides of a right-angled triangle in the following way: Hypotenuse (H) This is the longest side and is opposite the right- angle Opposite Side (O) This is the side opposite the angle in question Adjacent Side (A) This is the side adjacent (next to) the angle in question.

Label the sides of the right-angled triangles on the sheet.

dustonschoolmaths does trigonometry http://www.youtube.com/ watch?v=XyCdqyPFP50

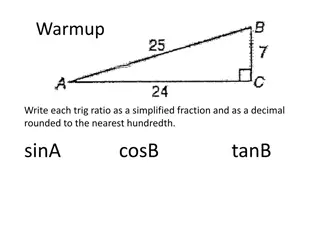
Calculate the length of side p. A Hyp p C H 46 p = adj cos p = 7 cos 46 p = 10.08 cm 7cm Adj

Calculate the size of angle Q. O T A 4.3m Opp tan Q = opp adj tan Q = 4.3 3.8 Q = tan-1 (4.3 3.8) Q = 49 Q 3.8m Adj

Answers 1. a = 12.03 cm b = 61.44 cm c = 41.80 cm d = 115.19 cm 3. 2.25 m 4. 48.2o 5. 9.21 m 2. a = 69.5 b = 33.5 c = 69.4 d = 54.4 Extension: 12.073 cm (3dp)

Show me and example of: - A hypotenuse - An opposite side - An adjacent side - A problem that can be solved using trigonometry - A triangle in which the tangent of the angle is 1 - A triangle in which the cosine is 0.5

What is the same/different about three triangles with sides 3, 4, 5 and 6, 8, 10 and 5, 12, 13 True/Never/Sometimes: - You can use trigonometry to find the missing length/angle in triangles

The image below is of a cuboid. Calculate the size of the angle between CE and EFGH. C EG = EH + HG = 4 + 3 = 25 EG = 25 = 5 cm B C D A 11cm 11cm G 3cm F ? E E G H ? cm 4cm

The image below is of a cuboid. Calculate the size of the angle between CE and EFGH. C B C D A O T A 11cm 11cm Opp tan ? = opp adj tan ? = 11 5 ? = tan-1 (11 5) ? = 66 G 3cm F ? E E G H 5 cm Adj 4cm

Answers 1. 10.2 2. a. 9.11 cm b. 19.2

Starter Find the lengths of the missing sides. Give your answer in surd form where appropriate. 14 cm 2 33 _____ cm 4 cm 6 ___ cm 8 cm 5 cm 4 5 ____ cm 4 cm 16 cm

Make sure you fill in your table as we go you ll need it later! Angle ( Degrees) 0 30 45 60 90 180 270 360 sin cos tan

Periodic Symmetrical

Periodic Symmetrical

Periodic

Remember: (You may want to copy these down!) O A O H H A sin cos tan

Lets start with an isosceles right-angled triangle with equal sides of 1 cm. These angles are equal and angles in a triangle sum to 180 . 45 1 cm 45 1 cm

Lets start with an isosceles right-angled triangle with equal sides of 1 cm. 45 2 cm 1 cm By Pythagoras Theorem, the hypotenuse is 2. 45 1 cm

sin 45 = _1_ 2 45 2 cm 1 cm 45 1 cm

sin 45 = _1_ 2 45 cos 45 = _1_ 2 2 cm 1 cm 45 1 cm

sin 45 = _1_ 2 45 cos 45 = _1_ 2 2 cm 1 cm tan 45 = 1 = 1 1 45 1 cm

sin 45 = 2 sin 45 = _1_ 2 2 45 cos 45 = 2 cos 45 = _1_ 2 2 2 cm 1 cm tan 45 = 1 = 1 1 45 1 cm Rationalising the denominators gives

Now lets look at an equilateral triangle with sides of 2 cm. 60 2 cm 2 cm 60 60 2 cm

Now lets look at an equilateral triangle with sides of 2 cm. By Pythagoras Theorem, the height is 3. 30 2 cm 3 cm 60 1 cm

sin 30 = 1 2 30 2 cm 3 cm 60 1 cm

sin 30 = 1 2 30 cos 30 = 3 2 2 cm 3 cm 60 1 cm

sin 30 = 1 2 30 cos 30 = 3 2 2 cm 3 cm tan 30 = _1_ 3 60 1 cm

Rationalising the denominator gives sin 30 = 1 2 30 cos 30 = 3 2 2 cm 3 cm tan 30 = _1_ 3 3 tan 30 = 3 60 1 cm

sin 60 = 3 2 30 2 cm 3 cm 60 1 cm

sin 60 = 3 2 30 cos 60 = 1 2 2 cm 3 cm 60 1 cm

sin 60 = 3 2 30 cos 60 = 1 2 2 cm 3 cm tan 60 = 3 1 60 1 cm

sin 60 = 3 2 30 cos 60 = 1 2 2 cm 3 cm tan 60 = 3 1 60 1 cm

Answers Question 1 a) d) - b) e) 1 2 c) f) -1 3 Question 2 a) 3 1 2 b) 3 Question 3 1 2 Question 4 a) 12 3 m b) 28 m Question 5 sin 270 sin 10 sin 135 sin 90

Trigonometry Help Flow Chart Is the triangle right-angled? Yes No Does the question involve any angles? Do you know a side and an opposite angle? Yes No No Yes Use Use trig ratios SOHCAHTOA Use the Cosine rule Use the Sine rule Pythagoras Theorem

Show me and example of: - A problem that can be solved using the sine rule - A problem that can be solved using the cosine rule - A triangle which you can find the area of

Group activity Put 3 triangles in each column to identify the method you would use to find the missing information. Make sure you can justify every triangle. Extension: How many can you solve?