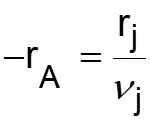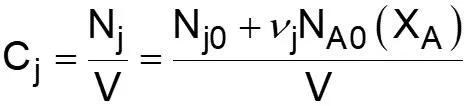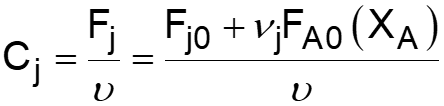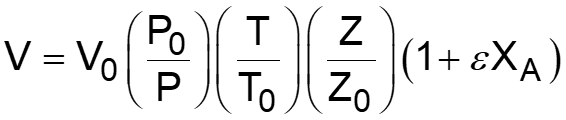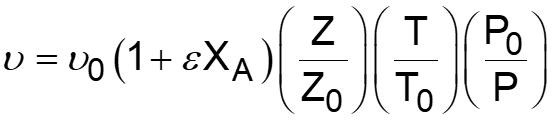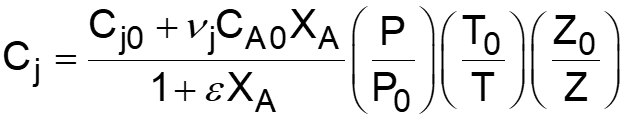Chemical Reactor Design Principles
Review: Derive –r
A
= f(X
A
)
Batch:
Flow:
Batch:
Flow:
Batch
&
Flow:
Now that C
j
is in terms of X
A
, we can write the rate law in terms of X
A
Review: Stoichiometric Tables
F
A0
F
B0
F
C0
F
D0
F
I
0
F
A
F
B
F
C
F
D
F
I
j
≡ stoichiometric coefficient
for products,
⊖
for reactants
In
Out
L5: Reactor Design Recipe and
Reactor Scale-Up (Sizing)
Goal
: Develop an algorithm that combines reactor design
equations with reaction rates for the design of different reactors
The Logic of Isothermal Reactor Design
1. Set up mole balance for
specific reactor
2. Derive design eq. in
terms of X
A
for each
reactor
Batch
CSTR
PFR
3. Put C
j
is in terms of
X
A
and plug into r
A
4. Plug r
A
into design eq and solve for the
time (batch) or volume (flow) required
for a specific X
A
Today and next week!
(We will always look
conditions where Z
0
=Z)
Batch Reactor Operation (1)
B
a
t
c
h
V
o
l
u
m
e
i
s
c
o
n
s
t
a
n
t
,
V
=
V
0
M
o
l
e
b
a
l
a
n
c
e
R
a
t
e
l
a
w
S
t
o
i
c
h
i
o
m
e
t
r
y
(
p
u
t
C
A
i
n
t
e
r
m
s
o
f
X
)
C
o
m
b
i
n
e
Calculate the time required for a conversion of X
A
in a constant V batch reactor
Batch Reactor Operation (2)
Calculate the time required for a conversion of X
A
in a constant V batch reactor
Evaluate
R
e
a
r
r
a
n
g
e
t
o
g
e
t
l
i
k
e
v
a
r
i
a
b
l
e
s
t
o
g
e
t
h
e
r
k
i
s
c
o
n
s
t
a
n
t
f
o
r
a
n
i
s
o
t
h
e
r
m
a
l
r
e
a
c
t
i
o
n
T
i
m
e
r
e
q
u
i
r
e
d
t
o
a
c
h
i
e
v
e
X
A
f
o
r
2
n
d
o
r
d
e
r
r
x
n
Batch Reactor Operation (3)
B
a
t
c
h
V
o
l
u
m
e
i
s
c
o
n
s
t
a
n
t
,
V
=
V
0
Calculate the time required for a conversion of X
A
in a constant V batch reactor
M
o
l
e
b
a
l
a
n
c
e
R
a
t
e
l
a
w
S
t
o
i
c
h
i
o
m
e
t
r
y
(
p
u
t
C
A
i
n
t
e
r
m
s
o
f
X
)
C
o
m
b
i
n
e
Mole balance as a function of conversion
Batch Reactor Operation (4)
Calculate the time required for a conversion of X
A
in a constant V batch reactor
Evaluate to solve for time
R
e
a
r
r
a
n
g
e
t
o
g
e
t
l
i
k
e
v
a
r
i
a
b
l
e
s
t
o
g
e
t
h
e
r
k
i
s
c
o
n
s
t
a
n
t
f
o
r
a
n
i
s
o
t
h
e
r
m
a
l
r
e
a
c
t
i
o
n
T
i
m
e
r
e
q
u
i
r
e
d
t
o
a
c
h
i
e
v
e
X
A
f
o
r
1
s
t
o
r
d
e
r
r
x
n
Mole balance as
in terms of X
A
:
Batch Reactor Operation (4)
Calculate the time required for a conversion of X
A
in a constant V batch reactor
0=ln(1)
Typical Cycle Time for a Batch
Polymerization
Total Cycle Time t
t
= t
f
+ t
e
+ t
R
+ t
c
Total Cycle Time t
t
for a batch process is much longer than the reaction time
because it takes time to set up, heat, and clean the reactor each time it is used
CSTR Operation (1)
Calculate the CSTR volume required to get a conversion of X
A
M
o
l
e
b
a
l
a
n
c
e
R
a
t
e
l
a
w
S
t
o
i
c
h
i
o
m
e
t
r
y
(
p
u
t
C
A
i
n
t
e
r
m
s
o
f
X
)
C
o
m
b
i
n
e
P
u
t
F
A
0
i
n
t
e
r
m
s
o
f
C
A
0
V
o
l
u
m
e
r
e
q
u
i
r
e
d
t
o
a
c
h
i
e
v
e
X
A
f
o
r
1
s
t
o
r
d
e
r
r
x
n
(
)
Scaling CSTRs
Space time
(residence time) required to
achieve X
A
for 1
st
order irreversible rxn
•
Chemical engineers are involved in scaling up a laboratory scale reaction
to the pilot plant scale or full-scale reactor
•
If one knows the volume of the pilot-scale reactor required to achieve X
A
,
how is this information used to achieve X
A
in a larger reactor?
k in the small reactor is the same as k in the bigger reactor
Want X
A
in the small reactor to be the same as X
A
in the bigger reactor
0
in the small reactor must be different from
0
in the bigger reactor
Suppose for a 1
st
order irreversible liquid-phase reaction:
So the reactor volume
V
must be proportional to the volumetric flow rate
0
How?
Scaling CSTRs with Spacetime
A
→ B -r
A
= kC
A
So if you know the spacetime
required to get a conversion of X
A
in a
CSTR, you can use that to achieve the same X
A
in a different size CSTR
1
s
t
o
r
d
e
r
r
e
a
c
t
i
o
n
r
a
t
e
What
is required to achieve a specific X
A
?
C
S
T
R
r
e
l
a
t
i
o
n
s
h
i
p
b
e
t
w
e
e
n
a
n
d
X
A
f
o
r
1
s
t
o
r
d
e
r
l
i
q
u
i
d
-
p
h
a
s
e
r
x
n
(
i
s
o
t
h
e
r
m
a
l
a
n
d
V
=
V
0
)
Space time
(residence time) required to
achieve X
A
for 1
st
order irreversible rxn
Rearrange to get X
A
in terms of
Damköhler Number, Da
Estimates the degree of conversion that can be obtained in a flow reactor
F
i
r
s
t
o
r
d
e
r
i
r
r
e
v
e
r
s
i
b
l
e
r
e
a
c
t
i
o
n
:
1
st
order
irreversible
reaction
S
e
c
o
n
d
o
r
d
e
r
i
r
r
e
v
e
r
s
i
b
l
e
r
e
a
c
t
i
o
n
:
2
nd
order
irreversible
reaction
H
o
w
i
s
X
A
r
e
l
a
t
e
d
t
o
D
a
i
n
a
f
i
r
s
t
o
r
d
e
r
i
r
r
e
v
e
r
s
i
b
l
e
r
e
a
c
t
i
o
n
i
n
a
f
l
o
w
r
e
a
c
t
o
r
?
Substitute
From
previous
slide:
I
f
D
a
<
0
.
1
f
o
r
t
h
i
s
1
s
t
o
r
d
e
r
i
r
r
e
v
e
r
s
i
b
l
e
r
x
n
i
n
a
f
l
o
w
r
e
a
c
t
o
r
,
t
h
e
n
Damköhler Number, Da
Estimates the degree of conversion that can be obtained in a flow reactor
Relate X
A
to Da for a 1
st
order irreversible rxn in
a flow reactor:
I
f
D
a
>
1
0
f
o
r
t
h
i
s
1
s
t
o
r
d
e
r
i
r
r
e
v
e
r
s
i
b
l
e
r
x
n
i
n
a
f
l
o
w
r
e
a
c
t
o
r
,
t
h
e
n
1
st
order
irreversible rxn
Sizing CSTRs for 2
nd
Order Rxns
•
Mole balance
•
Rate laws
•
Stoichiometry
•
Combine
or
Calculate the CSTR volume required to get a conversion of X
A
I
n
t
e
r
m
s
o
f
c
o
n
v
e
r
s
i
o
n
?
I
n
t
e
r
m
s
o
f
s
p
a
c
e
t
i
m
e
?
I
n
t
e
r
m
s
o
f
X
A
a
s
a
f
u
n
c
t
i
o
n
o
f
D
a
?
CSTRs in Series
Effluent of reactor 1 is input for
reactor 2,
no change in
A
first order reaction
is carried out isothermally using 2 CSTRs that are the
same size, and
and k are the same in both reactors (
& k
1
= k
2
= k)
R
e
l
a
t
e
C
A
2
t
o
C
A
1
,
k
,
&
1.
M
o
l
e
b
a
l
a
n
c
e
C
S
T
R
2
2.
R
a
t
e
l
a
w
C
S
T
R
2
3.
S
t
o
i
c
h
i
o
m
e
t
r
y
C
S
T
R
2
4.
C
o
m
b
i
n
e
f
o
r
C
S
T
R
2
Determine V
1
for 1
st
CSTR using our standard procedure. For 2
nd
CSTR:
Skip this step for now.
CSTRs in Series, C
A1
A first order reaction is carried out isothermally using 2 CSTRs that are the
same size, and
and k are the same in both reactors (
& k
1
= k
2
= k)
What is C
A1
in terms of
and k?
W
e
k
n
o
w
f
o
r
a
s
i
n
g
l
e
C
S
T
R
:
Put X
A
for 1
st
CSTR in
terms of C
A1
:
S
u
b
s
t
i
t
u
t
e
:
S
o
l
v
e
f
o
r
C
A
1
:
Effluent of reactor 1 is input for
reactor 2,
no change in
CSTRs in Series, C
A2
Effluent of reactor 1 is
input for reactor 2
A first order reaction is carried out isothermally using 2 CSTRs that are the
same size, and
and k are the same in both reactors (
& k
1
= k
2
= k)
Relate C
A2
to k &
1
st
order irreversible
rxn with V
1
= V
2
,
and k
1
= k
2
n CSTRs in Series
For n identical CSTRs, then:
H
o
w
i
s
c
o
n
v
e
r
s
i
o
n
r
e
l
a
t
e
d
t
o
t
h
e
#
o
f
C
S
T
R
s
i
n
s
e
r
i
e
s
?
Put C
An
in terms of X
An
(X
A
at the last CSTR):
1
st
order irreversible liquid phase
rxn run in n CSTRs with identical
V,
and k
1
st
order irreversible liquid-phase rxn run in n CSTRs with identical V,
and k
R
a
t
e
o
f
d
i
s
a
p
p
e
a
r
a
n
c
e
o
f
A
i
n
t
h
e
n
t
h
r
e
a
c
t
o
r
:
Isothermal CSTRs in Parallel
F
A0
F
A01
F
A02
same T, V,
Subscript i
denotes reactor i
F
A01
= F
A02
= … F
A0n
Mole Balance
Conversion achieved by any one of the reactors in parallel is the
same as if all the reactant were fed into one big reactor of volume V
Explore the fundamentals of chemical reactor design, including stoichiometry, reaction rates, and reactor scale-up. Learn to derive rate laws and design equations in terms of conversion for batch, CSTR, and PFR reactors. Discover the logic behind isothermal reactor design and calculation of required time or volume for a specific conversion. Slides courtesy of Prof. M. L. Kraft, Chemical & Biomolecular Engr. Dept, University of Illinois.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
L5-1 Review: Derive rA= f(XA) j stoichiometric coefficient for products, for reactants j r j = r A Relate all rjto Cj Batch: Flow: ( ) ( ) + + j A0 F N V N j A0 N V X F F X j j0 A j j0 A = = = = C C Relate all Cj(XA) to V( ) j j Batch: Flow: P P P P T T Z Z Z Z T T ( ) ( ) 0 0 = + = + V V 1 X 1 X Relate all V( ) to XA 0 A 0 A 0 0 0 0 Batch & Flow: + + C C X T T Z Z P P j0 A0 X j A 0 0 = C Put j 1 A 0 together Now that Cj is in terms of XA, we can write the rate law in terms of XA Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L5-2 Review: Stoichiometric Tables FA0 FB0 FC0 FD0 FI0 FA FB FC FD FI In Out b c d + + A B a C D a a Feed rate (mol/time) FA0 FB0 = FA0 FC0 = CFA0 FD0 = DFA0 FI0 = IFA0 FT0 Change in reactor (mol/time) -FA0XA BFA0XA CFA0XA DFA0XA --- FA0XA Effluent rate from reactor (mol/time) FA = FA0 (1 XA) FB = FA0 ( + BXA) FC = FA0 ( C+ CXA) FD = FA0 ( D+ DXA) FI=FI0 FT = FT0 + FA0XA Species A B C D I Total F F C C C C y y d a c a b a j0 j0 0 j0 j0 j stoichiometric coefficient for products, for reactants = = = = + = 1 J A0 A0 0 A0 A0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L5-3 L5: Reactor Design Recipe and Reactor Scale-Up (Sizing) Goal: Develop an algorithm that combines reactor design equations with reaction rates for the design of different reactors Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
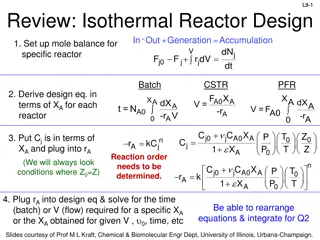
L5-4 The Logic of Isothermal Reactor Design In Out - 1. Set up mole balance for specific reactor +Generation =Accumulation dN dt V j + = F F rdV j0 j j Batch CSTR PFR 2. Derive design eq. in terms of XA for each reactor F X XA dXA 0 XA A0 -r A dX -r V V = A t =N V =FA0 0 A0 A -rA A + + C C X T T Z Z P P j0 A0 X j A 0 0 n j = C = r kC j A 1 3. Put Cj is in terms of XA and plug into rA (We will always look conditions where Z0=Z) A 0 n + + C C X T T Z Z P P j0 A0 X j A 0 0 = r k A 1 A 0 4. Plug rA into design eq and solve for the time (batch) or volume (flow) required for a specific XA Today and next week! Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L5-5 Batch Reactor Operation (1) A B -rA = kCA2 2nd order reaction rate Calculate the time required for a conversion of XA in a constant V batch reactor dX dt A = r N V Mole balance A0 A 2 = Rate law Ar kC A = (1 X ) Stoichiometry (put CA in terms of X) C C A A0 A ( )( d X 2 ) 2 A = N k C 1 X V Combine A0 A 0 A dt Batch Volume is constant, V=V0 ( A0 dt )( d X )2 2 A = N k C 1 X V A0 A 0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L5-6 Batch Reactor Operation (2) A B -rA = kCA2 2nd order reaction rate Calculate the time required for a conversion of XA in a constant V batch reactor dX kC N t d 2 ( ) 2 A = 1 X V Evaluate A 0 A 0 A 0 dX dt 1 V dX d dX dt 2 ( ) 2 2 A ( ) 2 0 A t = kC 1 X = k C 1 X A0 A A0 A C N A 0 A0 )2 ( A Rearrange to get like variables together = 1 X kC A0 A dX dX 1 k is constant for an isothermal reaction A A = = kC dt dt A0 2 2 ( ) ( ) kC 1 X 1 X A0 A A Time required to achieve XA for 2nd order rxn Integrate X t X 1 dX A 1 A A = t = dt kC 1 X 2 ( ) kC 1 X A0 A A0 0 0 A Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L5-7 Batch Reactor Operation (3) A B -rA = kCA 1st order reaction rate Calculate the time required for a conversion of XA in a constant V batch reactor dX dt A = r N V Mole balance A0 A = r k C Rate law A A = (1 X ) Stoichiometry (put CA in terms of X) C C A A0 A dX dt ( ) A = N k C 1 X V Combine A0 A 0 A Batch Volume is constant, V=V0 dX N dt ( ) A = kC 1 X V Mole balance as a function of conversion A0 A 0 A 0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L5-8 Batch Reactor Operation (4) A B -rA = kCA 1st order reaction rate Calculate the time required for a conversion of XA in a constant V batch reactor dX kC N t d in terms of XA: Mole balance as ( ) A = 1 X V Evaluate to solve for time A 0 A0 A 0 dX d 1 V dX dt ( ) A t ( ) 0 A = kC 1 X = kC 1 X A0 A A0 A C N A0 A0 dX dt ( ) A Rearrange to get like variables together = k 1 X A dX 1 X 1 k dX 1 X k is constant for an isothermal reaction A A = dt = kdt ( ) ( ) A A Time required to achieve XA for 1st order rxn 1 ln 1 x X Integrate t 1 k 1 dX 1 X A 1 k A = = ln t dt ( ) 1 X A A 0 0 = ( ) Remember: ln 1 x Confused about the integration? See the next slide Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L5-9 Batch Reactor Operation (4) A B -rA = kCA 1st order reaction rate Calculate the time required for a conversion of XA in a constant V batch reactor X Integrate t dX 1 X A 1 k A = dt ( ) A 0 0 1 k 1 k 1 k X 0 ( ) ( ) ( ) t 0 ( ) ( ) ( ) A = = - ln 1 X t ln 1 X ln 1 0 t 0 A A 0=ln(1) 1 k 1 k 1 ( ) ( ) = = ln 1 X t ln t A 1 X A 1 a = ( ) ln ln a Remember: Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L5-10 Typical Cycle Time for a Batch Polymerization Total Cycle Time tt for a batch process is much longer than the reaction time because it takes time to set up, heat, and clean the reactor each time it is used Activity 1. Charge feed to the reactor and agitate (tf) 2. Heat to reaction temperature (te) 3. Carry out reaction (tR) 4. Empty and clean reactor (tc) Total time excluding reaction Time (h) 1.5 - 3.0 0.2 2.0 (varies) 0.5 1.0 3.0 6.0 Total Cycle Time tt = tf + te + tR + tc Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L5-11 CSTR Operation (1) A B -rA = kCA Liquid-phase 1st order reaction rate Calculate the CSTR volume required to get a conversion of XA F X A0 r A = V Mole balance A = r k C Rate law A A = (1 X ) Stoichiometry (put CA in terms of X) C C A A0 A F X Put FA0 in terms of CA0 A0 1 X = V ( ) Combine k C A0 A Volume required to achieve XA for 1st order rxn ( = ) A0 0 C X X A 0 A = = V V ( ) ( ) kC 1 X k 1 X A0 A A Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L5-12 Scaling CSTRs Chemical engineers are involved in scaling up a laboratory scale reaction to the pilot plant scale or full-scale reactor If one knows the volume of the pilot-scale reactor required to achieve XA, how is this information used to achieve XA in a larger reactor? Suppose for a 1st order irreversible liquid-phase reaction: X X 0 A 0 A = = known: V want: V small bigger ( ) ( ) k 1 X k 1 X A A Want XA in the small reactor to be the same as XA in the bigger reactor k in the small reactor is the same as k in the bigger reactor 0 in the small reactor must be different from 0 in the bigger reactor So the reactor volume V must be proportional to the volumetric flow rate 0 How? X V X X Separate variables we will vary from those held constant A 0 A A 0 = = = V V ( ) ( ( ) ) X k 1 X k 1 X k 1 X 0 A A A Space time (residence time) required to achieve XA for 1st order irreversible rxn A = = V ( ) 0 k 1 X A Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L5-13 Scaling CSTRs with Spacetime X Space time (residence time) required to achieve XA for 1st order irreversible rxn A = ( ) k 1 X A A B -rA = kCA 1st order reaction rate So if you know the spacetime required to get a conversion of XA in a CSTR, you can use that to achieve the same XA in a different size CSTR What is required to achieve a specific XA? X X Rearrange to get XA in terms of A = A k = ( ) ( ) 1 X k 1 X A A ( ) = + = = + k X kX k kX X k X 1 k A A A A A CSTR relationship between and XA for 1st order liquid-phase rxn (isothermal and V = V0) + k = X A 1 k Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L5-14 Damk hler Number, Da = = A0 F enterin g flow rate of A A0 r V rate of reacti on at entrance reaction rate convectio = Da n rate Estimates the degree of conversion that can be obtained in a flow reactor First order irreversible reaction: r Da F 1st order irreversible reaction V k C C V k V A0 A0 = = = Da = k Da A0 0 0 A0 = V Substitute 0 Second order irreversible reaction: 2nd order irreversible reaction 2 kC V A0 r F V kC C V A 0 A 0 = = = = D a D a Da kC A0 A0 0 0 A 0 How is XA related to Da in a first order irreversible reaction in a flow reactor? From previous slide: + k Da + = = X X A A 1 k 1 Da Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L5-15 Damk hler Number, Da A0 r F V rate of reaction enterin at en trance reaction rate convection rat = = = Da g flow rate of A e A0 Estimates the degree of conversion that can be obtained in a flow reactor = k Da 1st order irreversible rxn Relate XA to Da for a 1st order irreversible rxn in a flow reactor: Da k = X = X A A + 1 Da + 1 k If Da<0.1 for this 1st order irreversible rxn in a flow reactor, then Da 0.1 = = = X X 0.091 A A + + 1 Da 1 0.1 If Da>10 for this 1st order irreversible rxn in a flow reactor, then Da 10 = = = X X 0.91 A A + + 1 Da 1 10 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L5-16 Sizing CSTRs for 2nd Order Rxns A B -rA = kCA2 Liquid-phase 2nd order reaction rate Calculate the CSTR volume required to get a conversion of XA F X C X A0 r 0 A0 r = = V Mole balance A A 2 = Ar kC Rate laws A = (1 X) C C Stoichiometry A A0 In terms of space time? C X V X 0 A0 1 = = = V Combine or 2 2 ( ) 2 ( ) kC X kC 1 X 0 A 0 A 0 ( ) 1 2 kC + 1 4 kC + A0 2 kC A0 = X In terms of conversion? A0 2nd order liquid irreversible reaction ( ) 2Da In terms of XA as a function of Da? 1 2Da + 1 4Da + = X = Da kC A0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L5-17 CSTRs in Series = CA0 0 Effluent of reactor 1 is input for reactor 2, no change in CA1 CA2 A first order reaction is carried out isothermally using 2 CSTRs that are the same size, and and k are the same in both reactors ( = = & k1 = k2 = k) Determine V1 for 1st CSTR using our standard procedure. For 2nd CSTR: F A2 F A1 = V 1. Mole balance CSTR2 A2 r kC = A2 r 2. Rate law CSTR2 A2 Skip this step for now. 3. Stoichiometry CSTR2 ( ) ( ) C C C C 0 A1 kC C = A2 A1 kC A2 4. Combine for CSTR2 = V or = A2 A2 C ( ) C C A1 kC A2 Relate CA2 to CA1, k, & = kC kC + = C C A2 A1 A2 A2 A2 A1 A2 C k ( ) A1 + + = = C k 1 C C A2 A1 A2 1 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L5-18 CSTRs in Series, CA1 CA1 CA2 CA0 0 = Effluent of reactor 1 is input for reactor 2, no change in A first order reaction is carried out isothermally using 2 CSTRs that are the same size, and and k are the same in both reactors ( = = & k1 = k2 = k) What is CA1 in terms of and k? We know for a single CSTR: Put XA for 1st CSTR in terms of CA1: k 1 k C C C C k A1 A1 = = = C C (1 X ) 1 X X 1 = X A1 A0 A1 A1 A1 A + 1 k A0 A0 C C C C k Solve for CA1: ( ) A1 A1 = + = = 1 k 1 1 k X Substitute: A1 + + 1 k A0 A0 C C C C C C C C C C ( ) A1 A1 A1 A1 A1 = + + = k 1 k k + C 1 + = 1 k 1 k 1 A0 A0 A0 A0 A0 C C 1 + A1 A0 = = C A1 1 k k A0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L5-19 CSTRs in Series, CA2 CA0 0 Effluent of reactor 1 is input for reactor 2 CA1 = CA2 A first order reaction is carried out isothermally using 2 CSTRs that are the same size, and and k are the same in both reactors ( = = & k1 = k2 = k) C 1 C A0 A1 = = C & C Relate CA2 to k & A2 A 1 + + k 1 k C 1 Substitute A 0 = C A 2 + + 1 k k 1 1st order irreversible rxn with V1 = V2, = and k1 = k2 C + A0 = C A2 2 ( ) 1 k Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L5-20 n CSTRs in Series CA0 0 CA1 = CA2 1st order irreversible liquid-phase rxn run in n CSTRs with identical V, and k C + A0 = C For n identical CSTRs, then: An n ( ) 1 k Rate of disappearance of A in the nth reactor: C + A0 An r = = kC k An n ( ) 1 k How is conversion related to the # of CSTRs in series? C Put CAn in terms of XAn (XA at the last CSTR): 1 ( ) A0 1 X = = C 1 X An A0 An n n ( ) ( ) + + 1 k 1 k 1 1st order irreversible liquid phase rxn run in n CSTRs with identical V, and k 1 1 = = X or 1 X An An n n ( ) ( ) + + 1 k 1 Da Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L5-21 Isothermal CSTRs in Parallel FA01 V Mole Balance X Subscript i denotes reactor i Ai r = A0i F FA0 i Ai FA02 same T, V, FA01 = FA02= FA0n X A r = V F X = X =...= X = X r r = A0 1 2 n A = = = ... An r r A1 A2 A total volume of all CSTRs # of CSTRs Volume of each CSTR V n = = V i A0 F n X V n Ai r = Ai F total molar flow rate # of CSTRs A0 n = = A0i F X A r = V F Molar flow rate of each CSTR A0 A Conversion achieved by any one of the reactors in parallel is the same as if all the reactant were fed into one big reactor of volume V Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
