Chemical Reactor Design Review: Mole Balances, Rate Data Analysis, Method of Excess
This content provides a comprehensive review of isothermal reactor design, including setting up mole balances, deriving design equations in terms of conversion, analyzing rate data to determine reaction order and rate constant, and applying the method of excess to evaluate reaction kinetics. Detailed explanations and steps for each topic are covered, along with visual aids for better understanding the concepts.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
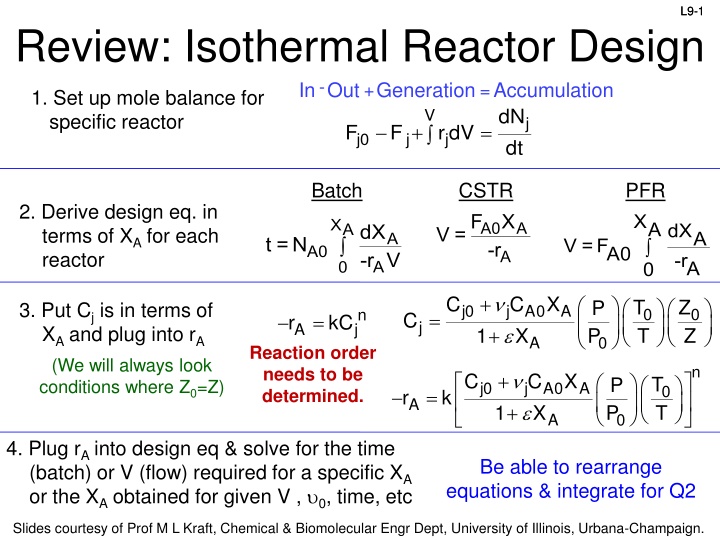
L9-1 L9-1 Review: Isothermal Reactor Design In Out - 1. Set up mole balance for specific reactor +Generation =Accumulation dN dt V j + = F F rdV j0 j j Batch CSTR PFR 2. Derive design eq. in terms of XA for each reactor F X XA dXA 0 XA A0 -r A dX -r V V = A t =N V =FA0 0 A0 A -rA A + + C C X T T Z Z P P 3. Put Cj is in terms of XA and plug into rA (We will always look conditions where Z0=Z) j0 A0 X j A 0 0 n j = C = r kC j A 1 A 0 Reaction order needs to be determined. n + C C X X T T P P j0 j A0 A 0 = r k A + 1 A 0 4. Plug rA into design eq & solve for the time (batch) or V (flow) required for a specific XA or the XA obtained for given V , 0, time, etc Be able to rearrange equations & integrate for Q2 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L9-2 L9-2 Review: Analysis of Rate Data Goal: determine reaction order, , and specific reaction rate constant, k Data collection is done in the lab so we can simplify BMB, stoichiometry, and fluid dynamic considerations Want ideal conditions well-mixed (data is easiest to interpret) Constant-volume batch reactor for homogeneous reactions: make concentration vs time measurements during unsteady-state operation Differential reactor for solid-fluid reactions: monitor product concentration for different feed conditions during steady state operation Method of Excess Differential method Integral method Half-lives method Initial rate method Differential reactor More complex kinetics Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L9-3 L9-3 Review: Method of Excess A + B products Suspect rate eq. -rA = kCA CB 1.Run reaction with an excess of B so CB CB0 2.Rate equation simplifies to rA = k CA where k =kACB k =kACB0 and can be determined 3.Repeat, but with an excess of A so that CA CA0 4.With excess A, rate simplifies to rA = k CB where k =kACA k =kACA0 5.Determine kA by measuring rA at known concentrations of A and B, where ) ( + r 1 1 s 3 A C = = k dm mol A C A B Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L9-4 L9-4 Review: Differential Method d F F r V N dt 0 0 dt Average slope alpha power dC + = j = r j0 j j j Where rA = kCA j Plot CA/ t vs t Determine dCA/dt from plot by graphical or numerical methods a) Draw rectangles on the graph. Then draw a curved line so that the area above the curve that is cut off of each rectangle approximately fills the unfilled area under the curve b) -dCA/dt is read using the value where the curve crosses a specified time Plot ln(-dCA/dt) vs ln CA 1. 2. Curved line represents dCA/dt dC C dt A = k Slope of line = A dC d 3. A = + l n l nk lnC Insert , dCA,p/dt, & corresponding CA,p A t Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L9-5 L9-5 Review: Integral Method A trial-and-error procedure to find reaction order Guess the reaction order integrate the differential equation Method is used most often when reaction order is known and it is desired to evaluate the specific reaction rate constants (k) at different temps to determine the activation energy Looking for the appropriate function of concentration corresponding to a particular rate law that is linear with time Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
dC dt L9-6 A = r For the reaction A products A dC dt For a zero-order reaction -rA = k A = k Plot of CA vs t is a straight line CA = C C kt A A0 t dC dt For a first-order reaction - rA = k CA ln (CA0/CA) Plot of ln(CA0/CA) vs t is a straight line A = kC A C C A0 = ln kt t A dC dt 2 For a second-order reaction - rA = k CA2 A = kC A 1/CA Plot of 1/CA vs t is a straight line 1 1 = kt C C t A A0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L9-7 L9-7 Review: Method of Half-lives Half-life of a reaction (t1/2): time it takes for the concentration of the reactant to drop to half of its initial value dC dt A products r = A = kC A kC A A ln (t1/2) 1 1 1 = t ( ) 1 1 k 1 C C A A0 Slope = 1- 1 2 = C C at t = t A A0 1 2 1 2 k 1 1 = 12 t ( ) 1 1 C A0 ln CA0 1 Plot ln(t1/2) vs ln CA0. Get a straight line with a slope of 1- 2 k 1 ( ) ( ) = + ln t ln 1 lnC 12 A0 ( ) 1 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L9-8 L9-8 Review: Method of Initial Rates When the reaction is reversible, the method of initial rates can be used to determine the reaction order and the specific rate constant Very little product is initially present, so rate of reverse reaction is negligible A series of experiments is carried out at different initial concentrations Initial rate of reaction is determined for each run Initial rate can be found by differentiating the data and extrapolating to zero time By various plotting or numerical analysis techniques relating -rA0 to CA0, we can obtain the appropriate rate law: = A0 r kC A0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L9-9 L9-9 Review: Differential Catalyst Bed r A: rate of reaction per unit mass of catalyst Conversion of reactants & change in reactant concentration in the bed is extremely small flow in - flow out + rate of gen = rate of accum. + = F F r W 0 L A0 Ae A F F C C A0 Ae 0 A0 Ae = = r A W W FAe FA0 When constant flow rate, 0 = : CA0 Cp Fp ( ) Product concentration 0 p C W C C 0 A0 Ae = = r A W The reaction rate is determined by measuring product concentration, Cp W Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L9-10 L9-10 L9: Reactor Design for Multiple Reactions Usually, more than one reaction occurs within a chemical reactor Minimization of undesired side reactions that occur with the desired reaction contributes to the economic success of a chemical plant Goal: determine the reactor conditions and configuration that maximizes product formation Reactor design for multiple reactions Parallel reactions Series reactions Independent reactions More complex reactions Use of selectivity factor to select the proper reactor that minimizes unwanted side reactions Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L9-11 L9-11 Classification of Multiple Reactions 1) Parallel or competing reactions B k1 A k2 C Desired product k1 k2 2) Series reactions A C B Desired product 3) Independent reactions Crude oil cracking k1 k2 A B C D k1 k2 4) Complex reactions + + + A B C D A C E Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L9-12 L9-12 Parallel Reactions Purpose: maximizing the desired product in parallel reactions ED RT kD 1 1 = D r A e C C 1 1 = D r k C C D (desired) D A B D A B A+B EU RT kU 2 2 = U r A e C C 2 2 = U r k C C U (undesired) U A B U A B E = + r D r U r Rate of disappearance of A: ED RT D A A e C r ( ) k T A RT = Ae EU RT 1 1 2 2 = + C A e C C A A B U B Define the instantaneous rate selectivity, SD/U E D A e C C RT D r r rate of formation of D rate of formation of U 1 1 = D U s D A B = = D U S E U U A e C C RT 2 2 A U B ( ) E E D RT U ( ) ( ) k k A A D D 1 2 1 2 1 2 1 2 = = D U S C C D U S e C C A B A B U U Goal: Maximize SD/U to maximize production of the desired product Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L9-13 L9-13 Maximizing SD/U for Parallel Reactions: Temperature Control ( E E D U D RT D U U A What reactor conditions and configuration maximizes the selectivity? Start with temperature (affects k): ) ( ) A 1 2 1 2 = S e C C A B b) If ED < EU a) If ED > EU ( ) E E ( ) D RT U E E E E D RT U E E D U 0 e 1 D U 0 e 1 RT RT Specific rate of desired reaction kD increases less rapidly with increasing T Use lower T to favor desired product formation (not so low that the reaction rate is tiny) Specific rate of desired reaction kD increases more rapidly with increasing T Use higher temperature to favor desired product formation Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L9-14 L9-14 Maximize SD/U for Parallel Reactions using Temperature D kD ( ) E E D RT U A A A D 1 2 = D U S e C A U kU U What reactor temperature maximizes the selectivity? ED = 20 kcal/mol, EU = 10 kcal/mol, T = 25 C (298K) or 100 C (373K) cal cal 20,000 10,000 mol mol cal 1.987 298K molK D 1 D U A U A cal cal 20,000 10,000 mol mol cal 1.987 373K molK D 1 D U A U A a) ED > EU T = 25 C (298K): ( ) A A A 8 D 2 1 2 = = 4.6 10 S e C D U S C A U T = 100 C (373K): kD/U ( ) A A A 6 D 2 1 2 = = 1.4 10 S e C D U S C A U SD/U is greater at 373K, higher temperature to favors desired product formation Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L9-15 L9-15 Maximizing SD/U for Parallel Reactions: Concentration kD ( ) E E D D RT U ( ) A A D 1 2 1 2 = D U S e C C A+B A B kU U U What reactor conditions and configuration maximizes the selectivity? Now evaluate concentration: a) 0 b) 0 1 2 1 2 1 2 1 2 1 2 1 2 C C A A Use large CA Use small CA c) 0 d) 0 1 2 1 2 1 2 1 2 1 2 1 2 C C B B Use large CB How do these concentration requirements affect reactor selection? Use small CB Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L9-16 L9-16 Concentration Requirements & Reactor Selection How do concentration requirements play into reactor selection? U kD D A+B kU CA 0 CB 0 CA0 0 CB0 0 CSTR: concentration is always at its lowest value (that at outlet) PFR PFR (or PBR): concentration is high at the inlet & progressively drops to the outlet concentration Semi-batch: concentration of one reactant (A as shown) is high at t=0 & progressively drops with increasing time, whereas concentration of B can be kept low at all times CB 0 Batch: concentration is high at t=0 & progressively drops with increasing time CA(t) CB(t) CA Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
kD L9-17 D High CA favors undesired product formation (keep CA low) High CA favors desired product formation A+B kU U PFR/PBR Side streams feed low CA Semi-batch reactor slowly feed A to large amt of B CA CSTRs in series Batch reactor High CB favors desired product formation CA When CA & CB are low (end time or position), all rxns will be slow High CB PFR/PBR CA CA High P for gas-phase rxn, do not add inert gas (dilutes reactants) CA 0 CB CA0 0 CB0 0 CSTR PFR/PBR w/ side streams feeding low CB CB Semi-batch reactor, slowly feed B to large amount of A CB CSTRs in series High CB favors undesired product formation (keep CB low) High CA PFR/PBR w/ high recycle PFR/PBR CB CB Dilute feed with inerts that are easily separated from product Low P if gas phase Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign. B consumed before leaving CSTRn
L9-18 L9-18 Different Types of Selectivity D r r rate of formation of D rate of formation of U = = D U S instantaneous rate selectivity, SD/U U S overall rate selectivity, D U F F Exit E x molar flow rate of desired product molar flow rate of undesir D = = D U S it ed pr oduct U N N Fi nal nal moles of desired product moles of undes D = = D U S Fi ir ed pr od ct u U D r r rate of formation of D rate of consumption of A instantaneous yield, YD (at any point or time in reactor) = = Y D A Y overall yield, D N F Evaluated at outlet Evaluated at tfinal D D = Y = Y batch flow D D N N F F A0 A A0 A Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L9-19 L9-19 Series (Consecutive) Reactions k1 k2 Time is the key factor here!!! A U D (desired) (undesired) Spacetime for a flow reactor Real time t for a batch reactor To maximize the production of D, use: CSTRs in series Batch or or PFR/PBR n and carefully select the time (batch) or spacetime (flow) Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L9-20 L9-20 Concentrations in Series Reactions -rA = k1CA rB,net = k1CA k2CB k1 k2 A C B How does CA depend on ? dF dV dC dV k1 A A = = = k C k C C C e 1 A 0 1 A A A 0 How does CB depend on ? B k C d V ( 1 d ) ( dF dC d V k1 B = = = k 2 B C k C e 2 B k C Substitute 1 A 0 1 A0 V 0 ) ( ) dC dC d k k B B 1 1 = + = k C e 2 B k C 2 B k C k C e A0 1 A0 ( ) k2 Use integrating factor (reviewed on Compass) k k d C e 1 2 e e k B d ( ) = k k C 1 A0 k C 2 1 = 1 A0 k C e B k 2 1 = C C C C C A0 A B Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L9-21 L9-21 Reactions in Series: Cj & Yield k1 = C C e B A A0 C A k k 1 2 e e k = C 1 A0 k C B k 2 1 = C C C C C A0 A B opt The reactor V (for a given 0) and that maximizes CB occurs when dCB/dt=0 ( 1 2 1 d k k ) 1 A0 k C dC k k B 1 2 = k e + = k e 0 2 k k 1 1 = ln opt k k 1 2 2 V = = 0 opt so V opt 0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
