Chemical Reactor Design: Unsteady State and Nonisothermal Reactors
Review: Unsteady State
Nonisothermal Reactor Design
An open system (for example, CSTR)
Goal: develop EB for unsteady state reactor
Review: Simplified EB for Well-Mixed
Reactors
Energy balance for
unsteady state reactor
with phase change:
Energy balance for
unsteady state reactor
without
phase change:
Total Energy Balance for unsteady state
Constant PV variation
Made following
substitutions &
solved for dT/dt:
Review: Unsteady State EB,
Liquid-Phase Reactions
F
o
r
l
i
q
u
i
d
-
p
h
a
s
e
r
e
a
c
t
i
o
n
s
,
o
f
t
e
n
C
p
=
i
C
p
i
i
s
s
o
s
m
a
l
l
i
t
c
a
n
b
e
n
e
g
l
e
c
t
e
d
When
C
p
can be neglected, then:
If the feed is well-mixed, it is convenient to use:
Plug these equations
& T
i0
= T
0
into the EB:
This equation for the EB is simultaneously solved with the mass
balance (design eq) for unsteady state, nonisothermal reactor design
Review: Nonisothermal Batch
Reactor Design
No flow, so:
0
Put the energy balance
in terms of conversion:
Solve with the batch reactor design
equation using an ODE solver (Polymath):
Review: Adiabatic Nonisothermal
Batch Reactor Design
For negligible
stirring work:
Substitute:
Rearrange
0
0
Solve for T:
Solve with the batch reactor design
equation using an ODE solver (Polymath)
Integrate &
solve for X
A
:
L17 Basic Catalysis & Reaction
Mechanisms
•
Though we have discussed the use of catalyst in a PBR, we have not
discussed the process of catalysis itself
•
An understanding of catalysis, the mechanisms, and catalytic reactor design
are the subject of the next few lectures
•
Catalyst properties
•
Steps involved in a catalytic reaction
•
Development of a rate law using steps in catalytic reaction
•
Different types of catalyst mechanisms
•
Design of catalytic reactors
Catalysts & Catalysis
•
~1/3 of the GNP of materials produced in the US involve a catalytic process
•
A
C
a
t
a
l
y
s
t
i
s
a
s
u
b
s
t
a
n
c
e
t
h
a
t
s
p
e
e
d
s
u
p
t
h
e
r
a
t
e
o
f
r
e
a
c
t
i
o
n
b
u
t
i
s
n
o
t
c
h
a
n
g
e
d
b
y
t
h
e
r
e
a
c
t
i
o
n
•
A catalyst lowers the energy barrier by promoting a different molecular
pathway (mechanism) for the reaction
Many catalyst are porous (high surface area)
•
H
o
m
o
g
e
n
e
o
u
s
c
a
t
a
l
y
s
i
s
:
c
a
t
a
l
y
s
t
i
s
i
n
s
o
l
u
t
i
o
n
w
i
t
h
a
t
l
e
a
s
t
1
r
e
a
c
t
a
n
t
•
H
e
t
e
r
o
g
e
n
e
o
u
s
c
a
t
a
l
y
s
i
s
:
m
o
r
e
t
h
a
n
1
p
h
a
s
e
,
u
s
u
a
l
l
y
s
o
l
i
d
a
n
d
f
l
u
i
d
o
r
s
o
l
i
d
a
n
d
g
a
s
i
s
p
r
e
s
e
n
t
.
R
e
a
c
t
i
o
n
o
c
c
u
r
s
a
t
s
o
l
i
d
/
l
i
q
u
i
d
o
r
g
a
s
i
n
t
e
r
f
a
c
e
.
catalyst
1. Mass transfer
of A to surface
2. Diffusion of A
from pore mouth to
internal catalytic
surface
3. Adsorption of
A onto catalytic
surface
4. Reaction on surface
5. Desorption of product
B from surface
6. Diffusion of B
from pellet interior
to pore mouth
7. Diffusion of B
from external
surface to the bulk
fluid (external
diffusion)
Steps in a Heterogeneous Catalytic
Reaction
C
h
1
0
a
s
s
u
m
e
s
s
t
e
p
s
1
,
2
,
6
&
7
a
r
e
f
a
s
t
,
s
o
o
n
l
y
s
t
e
p
s
3
,
4
,
a
n
d
5
n
e
e
d
t
o
b
e
c
o
n
s
i
d
e
r
e
d
Adsorption Step
A(g) + S
⇌ A
·S
S: open (vacant) surface site
A
·S: A bound to a surface site
The adsorption of A (gas phase) on an active site S is represented by:
A
I
-S-S-S-
Rate of adsorption = rate of attachment – rate of detachment
partial pressure of A
•
Rate is proportional to # of collisions with surface, which is a function of P
A
•
Rate is proportional to # of vacant (active) sites, C
v
, on the surface
•
Active site: site on surface that can form a strong bond with adsorbed species
Molar conc of vacant sites on surface
A
-S-S-S-
I
n
t
e
r
m
s
o
f
t
h
e
a
d
s
o
r
p
t
i
o
n
e
q
u
i
l
i
b
r
i
u
m
c
o
n
s
t
a
n
t
K
A
w
h
e
r
e
Equation
I
Site Balance
C
t
: Total number of active sites per unit mass of catalyst divided by
Avogadro’s # (mol/g
cat)
C
v
: Number of vacant sites per unit mass of catalyst divided by Avogadro’s #
C
t
= C
v
+ C
A
·S
+ C
B·S
Vacant
active site
Site balance:
In the absence of catalyst deactivation, assume the total number of
active sites remains constant:
W
e
w
i
l
l
u
s
e
t
h
e
s
i
t
e
b
a
l
a
n
c
e
e
q
u
a
t
i
o
n
t
o
p
u
t
C
v
i
n
t
e
r
m
s
o
f
m
e
a
s
u
r
a
b
l
e
s
p
e
c
i
e
s
C
v
i
s
n
o
t
m
e
a
s
u
r
a
b
l
e
,
b
u
t
t
h
e
t
o
t
a
l
n
u
m
b
e
r
o
f
s
i
t
e
s
C
t
c
a
n
b
e
m
e
a
s
u
r
e
d
Langmuir Isotherm Adsorption
Adsorption of carbon monoxide onto a surface:
CO + S
⇌
CO
·S
P
u
t
C
v
i
n
t
e
r
m
s
o
f
C
t
u
s
i
n
g
t
h
e
s
i
t
e
b
a
l
a
n
c
e
;
o
n
l
y
C
O
c
a
n
a
b
s
o
r
b
o
n
t
h
e
s
u
r
f
a
c
e
:
A
t
e
q
u
i
l
i
b
r
i
u
m
,
r
A
D
=
0
:
Determine the concentration of CO adsorbed on the surface at equilibrium
R
e
a
r
r
a
n
g
e
&
s
o
l
v
e
f
o
r
C
C
O
·
S
Insert into eq for C
CO
·S
from rxn rate
Solve for C
CO
·S
Concentration of CO adsorbed on
surface vs P
CO
→ Langmuir Isotherm
Surface Reaction Step
After the molecule is adsorbed onto the surface, it can react by a few different
mechanisms
1. Singe site mechanism: Only the site to which the reactant is absorbed is
involved in the reaction
A
I
-S-
⇌
B
I
-S-
A
·S
⇌
B·S
2. Dual site mechanism: Adsorbed reactant interacts with another vacant
site to form the product
A
I
-S-S-S
⇌
B
I
-S-S-S-
A
·S + S
⇌
S
+
B·S
Equation
II
a
Equation
II
b
3. Eley-Rideal mechanism: reaction between adsorbed reactant and a
molecule in the gas phase
⇌
C
I
-S-S-S-
A
·S + B(g)
⇌
C·S
Equation
II
c
Desorption Step
Products are desorbed into the gas phase
C
I
-S-S-S-
⇌
C
-S-S-S-
C
·S
⇌
C + S
Equation
III
N
o
t
e
t
h
a
t
t
h
e
d
e
s
o
r
p
t
i
o
n
o
f
C
i
s
t
h
e
r
e
v
e
r
s
e
o
f
t
h
e
a
d
s
o
r
p
t
i
o
n
o
f
C
A
l
s
o
t
h
e
d
e
s
o
r
p
t
i
o
n
e
q
u
i
l
i
b
r
i
u
m
c
o
n
s
t
a
n
t
K
D
,
C
i
s
t
h
e
r
e
c
i
p
r
o
c
a
l
o
f
t
h
e
a
d
s
o
r
p
t
i
o
n
e
q
u
i
l
i
b
r
i
u
m
c
o
n
s
t
a
n
t
K
C
S
u
b
s
t
i
t
u
t
i
n
g
1
/
K
C
f
o
r
K
D
,
C
i
n
t
h
e
r
a
t
e
e
q
u
a
t
i
o
n
f
o
r
p
r
o
d
u
c
t
d
e
s
o
r
p
t
i
o
n
g
i
v
e
s
:
Derive a Rate Law for Catalytic Rxn
•
Postulate catalytic mechanism, and then derive the rate law for that
mechanism
•
Assume pseudo-steady state hypothesis (rate of adsorption = rate of
surface reaction = rate of desorption)
•
No accumulation of species on the surface or near interface
•
Each species adsorbed on the surface is a reactive intermediate
•
Net rate of formation of species i adsorbed on the surface is 0, r
i
·S
=0
•
One step is usually rate-limiting
•
If the rate-limiting step could be sped up, the entire rxn would be faster
•
Although reactions involve all 7 steps, (for chapter 10) only adsorption,
surface reaction, or desorption will be rate limiting
•
T
h
e
s
u
r
f
a
c
e
r
e
a
c
t
i
o
n
s
t
e
p
i
s
r
a
t
e
l
i
m
i
t
i
n
g
~
7
0
%
o
f
t
h
e
t
i
m
e
!
•
Steps to derive the rate law
•
Select among types of adsorption, surface reaction, and desorption
•
Write rate laws for each individual step,
assuming all are reversible
•
Postulate which step is rate limiting
•
Use non-rate-limiting steps to eliminate the surface concentration
terms that cannot be measured
Consider A
⇌
B and assume the following mechanism is correct:
1. Adsorption:
2. Surface reaction:
A(g) + S
⇌ A
·S
A
·S + S
⇌
S
+
B·S
3. Desorption:
B
·S
⇌
B + S
We need to select one of these 3 reactions as the rate limiting step, then
derive the corresponding rate equation, and see if this rate eq matches
experimental data.
Which step is the most logical to start with?
a)
Adsorption
b)
Surface reaction
c)
Desorption
d)
None of the above
e)
Any of these would be “logical” - they all have equal probability of being
the rate limiting step
The surface reaction step as is rate limiting ~70% of the time
Consider A
⇌
B and assume the following mechanism is correct:
1. Adsorption:
2. Surface reaction:
A(g) + S
⇌ A
·S
A
·S + S
⇌
S
+
B·S
3. Desorption:
B
·S
⇌
B + S
Derive the rate equation for when the surface reaction is rate limiting (true
~70% of the time)
•
F
o
r
s
u
r
f
a
c
e
r
e
a
c
t
i
o
n
-
l
i
m
i
t
e
d
m
e
c
h
a
n
i
s
m
s
,
k
S
i
s
s
m
a
l
l
a
n
d
k
A
a
n
d
k
D
a
r
e
r
e
l
a
t
i
v
e
l
y
l
a
r
g
e
•
T
h
e
r
e
f
o
r
e
r
A
D
/
k
A
a
n
d
r
D
/
k
D
a
r
e
v
e
r
y
s
m
a
l
l
,
a
n
d
c
a
n
b
e
a
p
p
r
o
x
i
m
a
t
e
d
a
s
e
q
u
a
l
t
o
z
e
r
o
1
.
C
A
·
S
,
C
v
,
a
n
d
C
B
·
S
n
e
e
d
t
o
b
e
e
x
p
r
e
s
s
e
d
i
n
t
e
r
m
s
o
f
m
e
a
s
u
r
a
b
l
e
q
u
a
n
t
i
t
i
e
s
2
.
U
s
e
t
h
i
s
r
e
l
a
t
i
o
n
s
h
i
p
t
o
e
l
i
m
i
n
a
t
e
C
A
·
S
a
n
d
C
B
·
S
f
r
o
m
t
h
e
i
r
r
e
s
p
e
c
t
i
v
e
r
a
t
e
e
q
u
a
t
i
o
n
s
a
n
d
t
h
e
s
i
t
e
b
a
l
a
n
c
e
t
o
e
l
i
m
i
n
a
t
e
C
V
Consider A
⇌
B and assume the following mechanism is correct:
1. Adsorption
2. Surface reaction
3. Desorption
Derive the rate equation for when
the surface reaction is rate limiting
Use
r
AD
/k
A
=0 and r
D
/k
D
=0
to eliminate C
A
·S
and C
B·S
from their respective
rate equations and the site balance to eliminate C
V
Use r
AD
/k
A
=0 & r
AD
equation to solve for C
A
·S
:
Use r
D
/k
D
=0 & r
D
equation
to solve for C
B
·S
:
Consider A
⇌
B and assume the following mechanism is correct:
1. Adsorption
2. Surface reaction
3. Desorption
Derive the rate equation for when the surface reaction is rate limiting
r
AD
/k
A
=0 & r
D
/k
D
=0
U
s
e
s
i
t
e
b
a
l
a
n
c
e
t
o
s
o
l
v
e
f
o
r
C
V
:
M
a
k
e
s
u
b
s
t
i
t
u
t
i
o
n
s
f
o
r
C
A
·
S
&
C
B
·
S
,
s
o
l
v
e
f
o
r
C
v
Consider A
⇌
B and assume the following mechanism is correct:
1. Adsorption
2. Surface reaction
3. Desorption
Derive the rate equation for when the surface reaction is rate limiting
S
u
b
s
t
i
t
u
t
e
i
n
C
A
·
S
,
C
B
·
S
,
&
C
v
This is the rate equation in terms of measurable species and rate
constants for the mechanism given in the problem statement
Evaluating a Catalytic Reaction
Mechanism
•
Collect experimental data from test reactor
•
See if rate law is consistent with data
•
If not, then try other surface mechanism (i.e., dual-site
adsorption or Eley-Rideal) or choose a different rate-limiting
step (adsorption or desorption)
Consider A
⇌
B and assume the following mechanism is correct:
1. Adsorption
2. Surface reaction
3. Desorption
Now derive the rate equation for
when adsorption is rate limiting:
C
o
n
c
o
f
v
a
c
a
n
t
a
n
d
o
c
c
u
p
i
e
d
s
i
t
e
s
m
u
s
t
b
e
e
l
i
m
i
n
a
t
e
d
f
r
o
m
t
h
e
r
a
t
e
e
q
u
a
t
i
o
n
If adsorption is rate limiting, k
S
>>k
AD
, so
r
S
/k
S
can be approximated as
0
. Then:
If adsorption is rate limiting, k
D
>>k
AD
, so
r
D
/k
D
can be approximated as
0
. Then:
Need to put
C
B
·S
in
measureable terms
Consider A
⇌
B and assume the following mechanism is correct:
1. Adsorption
2. Surface reaction
3. Desorption
Now derive the rate equation for
when adsorption is rate limiting:
Conc of
vacant
and
occupied sites
must be eliminated from the rate eq
M
a
k
e
s
u
b
s
t
i
t
u
t
i
o
n
s
f
o
r
C
A
·
S
&
C
B
·
S
Solve for
C
v
using the site balance equation
S
u
b
s
t
i
t
u
t
e
C
v
i
n
t
o
t
h
e
e
x
p
r
e
s
s
i
o
n
f
o
r
C
B
·
S
:
S
u
b
s
t
i
t
u
t
e
C
B
·
S
i
n
t
o
C
A
·
S
:
Consider A
⇌
B and assume the following mechanism is correct:
1. Adsorption
2. Surface reaction
3. Desorption
Now derive the rate equation for
when adsorption is rate limiting:
U
s
e
t
h
e
s
e
e
q
s
t
o
r
e
p
l
a
c
e
C
A
·
S
&
C
v
i
n
r
A
D
:
F
a
c
t
o
r
o
u
t
C
t
:
The gas phase hydromethylation of toluene: C
6
H
5
CH
3
+ H
2
→ C
6
H
6
+ CH
4
is
to be carried out in a PBR. Plot the conversion and the partial pressures of
toluene, hydrogen and benzene as a function of catalyst weight.
F
A0
= 50 mol toluene/min, P
0
= 40 atm, T= 913K,
= 9.8 x 10
-5
kg
-1
, Feed is
30% toluene (species tol), 45% hydrogen (species H) and 25% inerts (I)
Rate law:
k= 0.00087 mol/atm
2
·kg cat·min
K
B
= 1.39 atm
-1
K
tol
= 1.038 atm
-1
M
o
l
e
b
a
l
a
n
c
e
:
R
a
t
e
l
a
w
:
S
t
o
i
c
h
i
o
m
e
t
r
y
:
1
N
e
e
d
c
o
n
c
e
n
t
r
a
t
i
o
n
s
i
n
t
e
r
m
s
o
f
p
r
e
s
s
u
r
e
The gas phase hydromethylation of toluene: C
6
H
5
CH
3
+ H
2
→ C
6
H
6
+ CH
4
is
to be carried out in a PBR. Plot the conversion and the partial pressures of
toluene, hydrogen and benzene as a function of catalyst weight.
F
A0
= 50 mol toluene/min, P
0
= 40 atm, T= 913K,
= 9.8 x 10
-5
kg
-1
, Feed is
30% toluene (species tol), 45% hydrogen (species H) and 25% inerts (I)
Rate law:
k= 0.00087 mol/atm
2
·kg cat·min
K
B
= 1.39 atm
-1
K
tol
= 1.038 atm
-1
Mole balance:
Rate law:
Stoichiometry:
U
s
e
t
h
e
E
r
g
u
n
e
q
u
a
t
i
o
n
t
o
e
v
a
l
u
a
t
e
y
:
Isothermal rxn &
=0, so:
N
e
e
d
a
n
e
q
u
a
t
i
o
n
f
o
r
P
B
&
P
H
The gas phase hydromethylation of toluene: C
6
H
5
CH
3
+ H
2
→ C
6
H
6
+ CH
4
is
to be carried out in a PBR. Plot the conversion and the partial pressures of
toluene, hydrogen and benzene as a function of catalyst weight.
F
A0
= 50 mol toluene/min, P
0
= 40 atm, T= 913K,
= 9.8 x 10
-5
kg
-1
, Feed is
30% toluene (species tol), 45% hydrogen (species H) and 25% inerts (I)
Rate law:
k= 0.00087 mol/atm
2
·kg cat·min
K
B
= 1.39 atm
-1
K
tol
= 1.038 atm
-1
Mole balance:
Rate law:
Stoichiometry:
F
i
n
a
l
l
y
,
c
a
l
c
u
l
a
t
e
t
h
e
k
g
c
a
t
w
h
e
r
e
P
0
=
1
a
t
m
:
Plug equation in boxes into Polymath to solve
Developing energy balances for unsteady state and nonisothermal reactors is essential for designing efficient chemical reactors. The energy balances involve terms such as heat flow, work done, energy accumulation, and mass flow, which impact the reactor's performance. By considering factors like phase change and heat capacity, these energy balances help in optimizing reactor designs for liquid-phase reactions and batch reactors.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
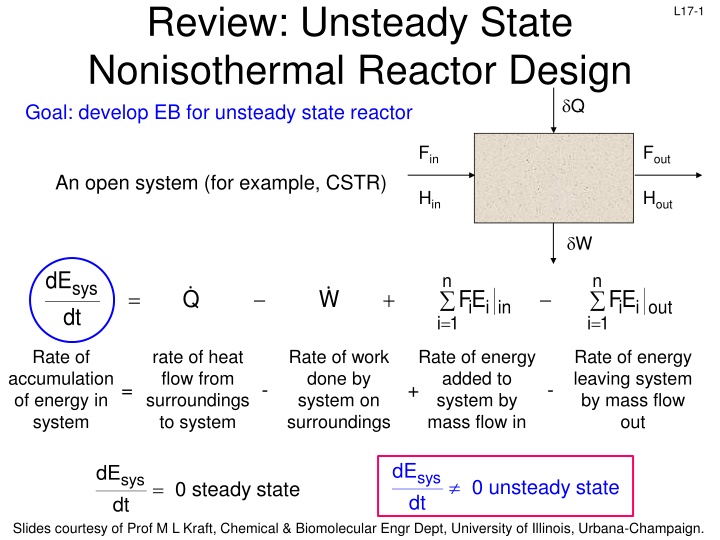
Review: Unsteady State Nonisothermal Reactor Design Goal: develop EB for unsteady state reactor L17-1 Q Fin Fout An open system (for example, CSTR) Hin Hout W dE n n sys dt = + Q W i i in FE i i out FE i 1 = i 1 = Rate of accumulation of energy in system rate of heat flow from surroundings to system Rate of work done by system on surroundings Rate of energy added to system by mass flow in Rate of energy leaving system by mass flow out = - + - dE dE sys dt sys dt 0 unsteady state = 0 steady state Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
Review: Simplified EB for Well-Mixed Reactors n n n S i i i i i 1 i 1 i 1 in out = = = L17-2 n dH dt dN dt d dt i i + = + Q W FH FH N H PV i i i 1 = Total Energy Balance for unsteady state Constant PV variation Made following substitutions & solved for dT/dt: dH dt dN dt dT dt i i dPV dt = i A r V = F F C i0 i pi = 0 n ( ) ( )( T r V ) + Q W F H H H Energy balance for unsteady state reactor with phase change: S i0 i i0 RX A dT dt i 1 = = n i pi NC i 1 = n ( ) ( )( T r V ) + Q W i0 pi F C T T H Energy balance for unsteady state reactor without phase change: S i0 RX A dT dt i 1 = = n i pi NC i 1 = Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
Review: Unsteady State EB, Liquid-Phase Reactions ( = n i pi i 1 L17-3 n ) ( )( T r V ) + Q W F C T T H i 1 S i0 pi i0 RX A d T = dt NC = For liquid-phase reactions, often Cp = iCpi is so small it can be neglected When Cp can be neglected, then: = = i pi A0 ps ps i pi i 1 n NC N C where C C is the heat capacity of the sol ution = If the feed is well-mixed, it is convenient to use: i0 F C = F C pi A0 ps ( ) ( )( T ) + Q W F C T N T C H r V dT dt Plug these equations & Ti0 = T0 into the EB: S A 0 p s i0 R X A = A0 p s This equation for the EB is simultaneously solved with the mass balance (design eq) for unsteady state, nonisothermal reactor design Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
Review: Nonisothermal Batch Reactor Design ( S i0 pi i0 i 1 n i pi i 1 = + 1 i Put the energy balance in terms of conversion: L17-4 n ) ( )( T r V ) + 0 Q W F C T T H RX A dT dt = = NC ( )( T ) Q W H r V S RX A No flow, so: n N C i p i = N N ( ) i0 = + = i & C = N N X where C i A0 i i A i p i P A 0 ( )( T r V ) + Q W H dT d S RX A = n t + N C C X A0 i p i p A = i 1 Solve with the batch reactor design equation using an ODE solver (Polymath): dX dt A = N r V A0 A Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
Review: Adiabatic Nonisothermal Batch Reactor Design ( )( S RX A n A0 i pi p A i 1 = T XA A dX C C X L17-5 0 0 ) For negligible stirring work: + Q W H T r V dT dt = i pi C C Substitute: Rearrange = ps + N C C X + dT = 0 T ( ) ( ) + H T C T T = pS p A X 0 T ( ) RX ) ( p R p R A0 ( ) C T C T T Integrate & solve for XA: p T 0 p 0 S S = = X X ( ) A A ( ) T ( ) H + H C T T RX RX R R ( ) C ( ) H T X H T X RX + 0 A RX 0 A = + = + Solve for T: T T T T 0 0 n C X p A p + i p C X C s A p i i 1 = XA Solve with the batch reactor design equation using an ODE solver (Polymath) dX r V A = t N A0 A 0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L17-6 L17 Basic Catalysis & Reaction Mechanisms Though we have discussed the use of catalyst in a PBR, we have not discussed the process of catalysis itself An understanding of catalysis, the mechanisms, and catalytic reactor design are the subject of the next few lectures Catalyst properties Steps involved in a catalytic reaction Development of a rate law using steps in catalytic reaction Different types of catalyst mechanisms Design of catalytic reactors Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L17-7 Catalysts & Catalysis ~1/3 of the GNP of materials produced in the US involve a catalytic process A Catalyst is a substance that speeds up the rate of reaction but is not changed by the reaction A catalyst lowers the energy barrier by promoting a different molecular pathway (mechanism) for the reaction Homogeneous catalysis: catalyst is in solution with at least 1 reactant Heterogeneous catalysis: more than 1 phase, usually solid and fluid or solid and gas is present. Reaction occurs at solid/liquid or gas interface. Many catalyst are porous (high surface area) catalyst Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
Steps in a Heterogeneous Catalytic Reaction L17-8 7. Diffusion of B from external surface to the bulk fluid (external diffusion) 1. Mass transfer of A to surface 2. Diffusion of A from pore mouth to internal catalytic 6. Diffusion of B from pellet interior to pore mouth 3. Adsorption of A onto catalytic surface surface 5. Desorption of product B from surface 4. Reaction on surface Ch 10 assumes steps 1,2,6 & 7 are fast, so only steps 3, 4, and 5 need to be considered Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L17-9 Adsorption Step The adsorption of A (gas phase) on an active site S is represented by: A A I A(g) + S A S -S-S-S- -S-S-S- S: open (vacant) surface site Rate of adsorption = rate of attachment rate of detachment r k P C = partial pressure of A Rate is proportional to # of collisions with surface, which is a function of PA Rate is proportional to # of vacant (active) sites, Cv, on the surface Active site: site on surface that can form a strong bond with adsorbed species A S: A bound to a surface site Molar conc of vacant sites on surface k C Conc of sites occupied by A A S AD A A v A k k A In terms of the adsorption equilibrium constant KA where = K A A k k A = = AD r A A k P C k C AD r k P C C A S A S v A A A v A C A S K = Equation I AD r k P C A A v A Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L17-10 Site Balance Ct: Total number of active sites per unit mass of catalyst divided by Avogadro s # (mol/g cat) Cv: Number of vacant sites per unit mass of catalyst divided by Avogadro s # Active site occupied by A Active site occupied by B Vacant active site A B Surface Cv is not measurable, but the total number of sites Ct can be measured In the absence of catalyst deactivation, assume the total number of active sites remains constant: Site balance: Ct = Cv + CA S + CB S We will use the site balance equation to put Cv in terms of measurable species Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L17-11 Langmuir Isotherm Adsorption Adsorption of carbon monoxide onto a surface: CO + S CO S COS C K k k A = = AD r k CO P C K = AD r A CO k P C k CO S C A v A v A A A Determine the concentration of CO adsorbed on the surface at equilibrium COS C K = = AD r 0 k CO P C At equilibrium, rAD = 0: A v A COS C K Rearrange & solve for CCO S = CO S C A CO K P C = CO v P C v A Put Cv in terms of Ct using the site balance; only CO can absorb on the surface: C C C = + t CO S v C C C = = COS A CO C K P = Insert into eq for CCO S from rxn rate ( ) t COS C C Solve for CCO S t v CO S CO S C A CO K P C v = CO S C A CO K P C A CO K P C CO S C + = CO S C A CO K P CO S C A CO K P C t t A CO K P 1 K P + Concentration of CO adsorbed on surface vs PCO Langmuir Isotherm t = COS C A CO Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L17-12 Surface Reaction Step After the molecule is adsorbed onto the surface, it can react by a few different mechanisms 1. Singe site mechanism: Only the site to which the reactant is absorbed is involved in the reaction A I -S- -S- k k C B I S B S K = = where K S r k C A S B S A S S S S S Equation IIa 2. Dual site mechanism: Adsorbed reactant interacts with another vacant site to form the product A I -S-S-S -S-S-S- 3. Eley-Rideal mechanism: reaction between adsorbed reactant and a molecule in the gas phase A S + B(g) C S A I -S-S-S A S + S S+ B S = B C C B S K v S r k C C I Equation IIb A S S v S B C C CS K = S r k C P Equation IIc I -S-S-S- A S B S S Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L17-13 Desorption Step Products are desorbed into the gas phase C S C + S = Equation III C C k k P C K D C v = where K D,C r k C I -S-S-S- -S-S-S- D,C CS D D D,C Note that the desorption of C is the reverse of the adsorption of C r = AD,C r D,C Also the desorption equilibrium constant KD,C is the reciprocal of the adsorption equilibrium constant KC 1 = K D,C K C Substituting 1/KC for KD,C in the rate equation for product desorption gives: = D,C r k C C C K P C CS D v Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L17-14 Derive a Rate Law for Catalytic Rxn Postulate catalytic mechanism, and then derive the rate law for that mechanism Assume pseudo-steady state hypothesis (rate of adsorption = rate of surface reaction = rate of desorption) No accumulation of species on the surface or near interface Each species adsorbed on the surface is a reactive intermediate Net rate of formation of species i adsorbed on the surface is 0, ri S=0 One step is usually rate-limiting If the rate-limiting step could be sped up, the entire rxn would be faster Although reactions involve all 7 steps, (for chapter 10) only adsorption, surface reaction, or desorption will be rate limiting The surface reaction step is rate limiting ~70% of the time! Steps to derive the rate law Select among types of adsorption, surface reaction, and desorption Write rate laws for each individual step, assuming all are reversible Postulate which step is rate limiting Use non-rate-limiting steps to eliminate the surface concentration terms that cannot be measured Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L17-15 Consider A B and assume the following mechanism is correct: C A S K = AD r k P C A(g) + S A S 1. Adsorption: A A v A C C B S K v = S r k C C A S + S S+ B S 2. Surface reaction: A S S v S P C B K v = D r k C B S B + S 3. Desorption: BS D D We need to select one of these 3 reactions as the rate limiting step, then derive the corresponding rate equation, and see if this rate eq matches experimental data. Which step is the most logical to start with? a) Adsorption b) Surface reaction c) Desorption d) None of the above e) Any of these would be logical - they all have equal probability of being the rate limiting step The surface reaction step as is rate limiting ~70% of the time Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L17-16 Consider A B and assume the following mechanism is correct: C A S K = AD r k P C A(g) + S A S 1. Adsorption: A A v A C C B S K v = S r k C C A S + S S+ B S 2. Surface reaction: A S S v S P C B K v = D r k C B S B + S 3. Desorption: BS D D Derive the rate equation for when the surface reaction is rate limiting (true ~70% of the time) r' r k C = = 1. CA S, Cv, and CB S need to be expressed in terms of measurable quantities C C BS K v C A S A S S v S For surface reaction-limited mechanisms, kS is small and kA and kD are relatively large Therefore rAD/kA and rD/kD are very small, and can be approximated as equal to zero 2. Use this relationship to eliminate CA S and CB S from their respective rate equations and the site balance to eliminate CV Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L17-17 Consider A B and assume the following mechanism is correct: 3. Desorption 1. Adsorption 2. Surface reaction = C P C C C A S K B K v B S K v = = AD r k P C D r k C S r k C C BS A S A A v D S v A D S C C Derive the rate equation for when the surface reaction is rate limiting BS K v = = r' S r k C C A S A S v S Use rAD/kA =0 and rD/kD =0 to eliminate CA S and CB S from their respective rate equations and the site balance to eliminate CV Use rAD/kA =0 & rAD equation to solve for CA S: C A S K = AD r k P C A A v D C C AD r k A S K = C A A K P C = P C A S K = = 0 P C A S v A v A v A A A P C Use rD/kD =0 & rD equation to solve for CB S: B K v = D r k C BS D D D r k P C P C B K v B K v = = = 0 C C BS BS D D D Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L17-18 Consider A B and assume the following mechanism is correct: 3. Desorption 1. Adsorption 2. Surface reaction = C P C C C A S K B K v B S K v = = AD r k P C D r k C S r k C C BS A S A A v D S v A D S Derive the rate equation for when the surface reaction is rate limiting C C BS K v = = r' S r k C C A S A S v S P C B K v = C = rAD/kA =0 & rD/kD =0 C A A K P C BS A S v D + = + C C C C Use site balance to solve for CV: A S B S t v Make substitutions for CA S & CB S, solve for Cv P C K P C K + = 1 K P + = C C C C A S B S v t P C B v B K v = + + = C C C A A K P C C v t A A v v v t D D C P K t B = C 1 K P + C C v v A A t P K B + D A A D Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L17-19 Consider A B and assume the following mechanism is correct: 3. Desorption 1. Adsorption 2. Surface reaction = C P C C C A S K B K v B S K v = = AD r k P C D r k C S r k C C BS A S A A v D S v A D S Derive the rate equation for when the surface reaction is rate limiting P C C K C t + B v = = C = C A A K P C BS v A S v 1 K P + P K D A A B D C C BS K v = = r' S r k C C Substitute in CA S, CB S, &Cv A S A S v S 2 2 C C P t + t + B = = r' S r k A A K P A S 1 K P + 1 K P + P K S D K K 2 K P P K A A B D A A B D C P t + B = = r' S r k A S A A 1 K P + P K S D K K A A B D This is the rate equation in terms of measurable species and rate constants for the mechanism given in the problem statement Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
Evaluating a Catalytic Reaction Mechanism L17-20 Collect experimental data from test reactor See if rate law is consistent with data If not, then try other surface mechanism (i.e., dual-site adsorption or Eley-Rideal) or choose a different rate-limiting step (adsorption or desorption) Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L17-21 Consider A B and assume the following mechanism is correct: 3. Desorption 1. Adsorption 2. Surface reaction = C P C C C A S K B K v B S K v = = AD r k P C D r k C S r k C C BS A S A A v D S v A D S C Now derive the rate equation for when adsorption is rate limiting: Conc of vacant and occupied sites must be eliminated from the rate equation If adsorption is rate limiting, kS>>kAD, so rS/kS can be approximated as 0. Then: = S K A S = = r' AD r k P C A A A v K A S r k C C C C B K S v B S v = = 0 C C S r k C C A S v S A S v S S C C C Need to put CB S in measureable terms B S K v B S K = = C C C A S v A S S S If adsorption is rate limiting, kD>>kAD, so rD/kD can be approximated as 0. Then: D r k P C P C P C B K v B K v = = = B K v 0 C C = D r k C B S B S D B S D D D D Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L17-22 Consider A B and assume the following mechanism is correct: 3. Desorption 1. Adsorption 2. Surface reaction = C P C C C A S K B K v B S K v = = AD r k P C D r k C S r k C C BS A S A A v D S v A D S C Now derive the rate equation for when adsorption is rate limiting: A S = = r' AD r k P C A A A v K A Conc of vacant and occupied sites must be eliminated from the rate eq C C = B S D K Make substitutions for CA S & CB S P C Solve for Cv using the site balance equation B S K B v = C A S S C P C B S K C P K K B K v = + + C C = + + C C C C t v t v A S B S S D t P P K P C P C = C B B B v B K v = + + = + + v C C 1 C C P K t v t v B B S D K K K K + + 1 D S D D S D D Substitute Cv into the expression for CB S: P C P C Substitute CB S into CA S: B P t = B t C = C B S A S P K P P K B B + + B B K 1 + + K K 1 D S D S D K K K K D S D D Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L17-23 Consider A B and assume the following mechanism is correct: 3. Desorption 1. Adsorption 2. Surface reaction = C P C C C A S K B K v B S K v = = AD r k P C D r k C S r k C C BS A S A A v D S v A D S Now derive the rate equation for when adsorption is rate limiting: P C P K K 1 K K C A S = = r' AD r k P C A A A v K A P C C B t B P t t = = C C = C A S B S v P P K P K P K B B B B B B + + 1 + + + + K 1 S D D S D K K S D K K D S D D D Use these eqs to replace CA S & Cv in rAD: P C P C A B t B t = AD r k A P P K P P K B + + B K B 1 + + K S D K K 1 A S D K K K D S D D k P P Factor out Ct: A B = AD r k C A t P P K P P K B B + + B K B 1 + + K K K 1 A S D S D K K K D S D D Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L17-24 The gas phase hydromethylation of toluene: C6H5CH3 + H2 C6H6 + CH4 is to be carried out in a PBR. Plot the conversion and the partial pressures of toluene, hydrogen and benzene as a function of catalyst weight. FA0 = 50 mol toluene/min, P0 = 40 atm, T= 913K, = 9.8 x 10-5 kg-1, Feed is 30% toluene (species tol), 45% hydrogen (species H) and 25% inerts (I) kP P k= 0.00087 mol/atm2 kg cat min KB = 1.39 atm-1 Ktol= 1.038 atm-1 ' H tol = r Rate law: T 1 K P + + ' tol r F 1 X 1 + B B K P tol tol kP P dX dW ' H tol = tol r Rate law: = Mole balance: T 1 K P + + + B B K P tol tol A0 1 X 1 P P T T P P 1 C tol tol 0 = C C = C C Stoichiometry: T T0 tol tol,0 X X tol 0 tol 0 Need concentrations in terms of pressure P V n RT = tol,0 P RT P RT tol = P C RT = = C tol tol tol tol,0 tol tol tol Total P tol,0 P RT P RT 1 X 1 + P P 1 X 1 + 0.3 1 P P tol tol tol = = P tol,0 P y where y= tol X X tol 0 tol 0 Total P at inlet tol,0 F F ( ) = = = = = y 0.3 0.3 0 0 = y 1 1 1 1 0 = + = Tol,0 tol,0 T0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L17-25 The gas phase hydromethylation of toluene: C6H5CH3 + H2 C6H6 + CH4 is to be carried out in a PBR. Plot the conversion and the partial pressures of toluene, hydrogen and benzene as a function of catalyst weight. FA0 = 50 mol toluene/min, P0 = 40 atm, T= 913K, = 9.8 x 10-5 kg-1, Feed is 30% toluene (species tol), 45% hydrogen (species H) and 25% inerts (I) kP P k= 0.00087 mol/atm2 kg cat min KB = 1.39 atm-1 Ktol= 1.038 atm-1 kP P r 1 K P + + ) 0.3 40atm 12atm = ' H tol = r Rate law: T 1 K P + = + B B K P tol tol ' tol r F dX dW ' tol H tol = Rate law: Mole balance: T B B K P A0 tol tol = tol,0 = 0 = y 0.3 0 P P ( ( ) = 1 X P tol,0 P = y where y= Stoichiometry: tol tol 0 = tol,0 P y P tol,0 P tol,0 0 Use the Ergun equation to evaluate y: )1 2 ( )( )12 ( = 1 X P tol,0 P 1 W Isothermal rxn & =0, so: = y 1 W tol tol Need an equation for PB & PH ( B tol,0 tol P P X = F ( ) 0.45 0.3 H2 F ) = = = = y P tol,0 P X y 1.5 H H tol H2 2 2 tol Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L17-26 The gas phase hydromethylation of toluene: C6H5CH3 + H2 C6H6 + CH4 is to be carried out in a PBR. Plot the conversion and the partial pressures of toluene, hydrogen and benzene as a function of catalyst weight. FA0 = 50 mol toluene/min, P0 = 40 atm, T= 913K, = 9.8 x 10-5 kg-1, Feed is 30% toluene (species tol), 45% hydrogen (species H) and 25% inerts (I) k= 0.00087 mol/atm2 kg cat min KB = 1.39 atm-1 Ktol= 1.038 atm-1 kP P ' H tol = r Rate law: T 1 K P + = + B B K P tol tol ' tol r F = tol,0 = 0 dX dW kP P ' tol H tol = = y 0.3 0 r Rate law: Mole balance: T 1 K P + + B B K P A0 tol tol )1 2 ( )( = tol,0 P 12atm ) tol y = 1 X Stoichiometry: P tol,0 P 1 W tol tol )12 ( ( ( ) = = y 1 W P tol,0 P 1.5 X = P tol,0 P X y H B tol 2 ( ) Finally, calculate the kg cat where P0 = 1atm: ( ) 12 P P 1 1atm 40atm ) )12 ( 5 1 = ( = 9.8 10 1 W 1 kg W 0 5 1 = 9.8 10 = 0.000625 Plug equation in boxes into Polymath to solve kg W W 10197.7kg final Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L17-27 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L17-28 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
L17-29 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
