Understanding Extreme Value Theory in Civil Engineering
Introduction to Extreme Value Theory by Gregory S. Karlovits and Emil Julius Gumbel. Exploring the importance of extreme values in civil engineering, Gumbel's EV questions, seeking models for extreme behavior, and lecture outlines on order statistics and extreme value theorems. The discussion includ
1 views • 48 slides
Understanding Complex Numbers and Functions in Mathematics
Explore the concept of complex numbers, their operations like addition, subtraction, and multiplication, as well as De Moivre's theorem for raising complex numbers to powers. Dive into solving problems using complex numbers and understanding functions, algebra, and the remainder and factor theorems
12 views • 45 slides
Understanding Continuity and Differentiability in Mathematics for Grade XII
Derivatives play a crucial role in engineering and science, helping analyze the behavior of dynamic systems. This unit delves into the concept of continuity and differentiability, exploring the geometric interpretation of derivatives, the chain rule, differentiation of algebraic functions, and the s
1 views • 18 slides
Understanding Extreme Value Theory in Civil Engineering
Introduction to Extreme Value Theory (EVT) in civil engineering focusing on the analysis of extremes such as shear strength, slope stability, and load factors. The theory, exemplified by Emil Julius Gumbel, questions the likelihood of individual observations falling outside expected distributions. E
10 views • 49 slides
Understanding Conditional Probability and Bayes Theorem
Conditional probability relates the likelihood of an event to the occurrence of another event. Theorems such as the Multiplication Theorem and Bayes Theorem provide a framework to calculate probabilities based on prior information. Conditional probability is used to analyze scenarios like the relati
1 views • 5 slides
Evolution of Mathematical Theories and Proof Systems
Development of mathematical theories such as model theory, proof theory, set theory, recursion theory, and computational complexity is discussed, starting from historical perspectives with Dedekind and Peano to Godel's theorems, recursion theory's golden age in the 1930s, and advancements in proof t
1 views • 29 slides
Concurrent Interpretations of Authorization Logic
Explore the concepts of authorization logic through discussions on policy enforcement, permissions, logical implications, and security theorems in the context of a scenario involving Alice, UdS Students, and printing permissions.
0 views • 50 slides
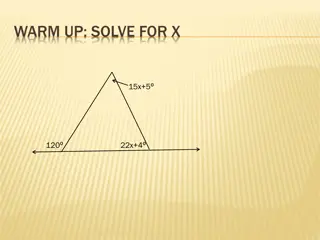
Exploring Polygon Angles in Geometry
Explore the interior and exterior angle measures of polygons, understand theorems related to polygon angles, classify polygons based on their properties, and solve problems involving regular polygons in this geometry chapter slideshow. The content covers key concepts such as the sum of interior angl
1 views • 41 slides
Understanding Sequences and Series of Functions in Real Analysis
Real analysis delves into the study of real numbers, sequences, series, and functions, exploring properties such as convergence, limits, continuity, differentiability, and integrability. This field scrutinizes the behavior of real-valued functions and their convergence types, including pointwise and
1 views • 11 slides
Understanding Real Numbers and Euclid's Division Algorithm
Explore the concept of real numbers, created by S.N. Mishra, and learn how to find the Highest Common Factor (HCF) using Euclid's Division Algorithm. Follow examples and theorems to deepen your understanding, including factorizing large numbers and proving the irrationality of 2. Dive into practical
0 views • 11 slides
Insights on Computational Complexity Threshold Results
Exploring the challenges in proving major lower bounds for computational complexity, focusing on the Hardness Magnification and Minimum Circuit Size Problem (MCSP). Discusses the difficulties in proving weak and strong LBs, highlighting recent theorems and barriers that impact progress in the field.
0 views • 21 slides
Mathematical Definitions and Theorems Illustrated
In this collection of images, various mathematical concepts are visually presented, including definitions, theorems, and proofs. The slides cover a range of topics in a structured manner, providing a concise overview of key mathematical principles. From foundational definitions to detailed proofs, t
0 views • 12 slides
Understanding Circles: Tangents, Inscribed Angles, and Theorems
Explore the concept of circles in geometry, focusing on tangent lines, inscribed angles, and related theorems. Understand the properties of tangents, relationships between angles and arcs, and how to apply theorems in circle problems. Visual examples and explanations included.
1 views • 19 slides
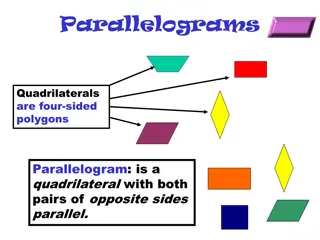
Understanding Parallelograms: Properties, Theorems, and Tests
Parallelograms are four-sided polygons with unique properties that include having both pairs of opposite sides parallel. Explore key theorems, tests, and properties of parallelograms such as opposite side and angle congruency, diagonal bisecting, and conditions for identifying a quadrilateral as a p
1 views • 19 slides
Understanding the Conjugate Beam Method in Structural Analysis
The Conjugate Beam Method is a powerful technique in structural engineering, derived from moment-area theorems and statical procedures. By applying an equivalent load magnitude to the beam, the method allows for the analysis of deflections and rotations in a more straightforward manner. This article
1 views • 11 slides
Turing Machine Variants and Equivalence Theorems Summary
Explore different variants of Turing machines, such as stay-put TMs and multi-tape TMs, along with key results like the equivalence theorems. Understand the idea behind simulating multi-tape TMs with single-tape TMs and how different models are related. Dive into the proofs and implications of these
0 views • 14 slides
Geometry Investigations and Theorems
Explore various circle theorems and investigations involving angles, tangents, radii, and circumferences. Discover the relationships between angles at the center and circumference, the properties of tangents, and the angle measurements within a circle. Engage in investigations to understand the sign
6 views • 26 slides
Understanding Circle Theorems and Equations of Circles
Explore circle theorems and equations of circles in geometry, including concepts like opposite angles in cyclic quadrilaterals, angles on a straight line, and important theorems like the perpendicular bisector of a chord passing through the center of a circle. Learn how to apply these theorems to fi
0 views • 12 slides
Comprehensive Mathematics Prior Learning Overview
This comprehensive overview delves into key mathematical concepts, including geometry, equations, quadratics, and circle theorems. It covers topics such as similarity, congruence, vectors, and algebraic manipulation, preparing students for more complex problem-solving and geometric proofs. The conte
0 views • 6 slides
Understanding Number Theory and Cryptography for Security
Explore the significance of number theory in cryptography, focusing on modular arithmetic, divisors, prime numbers, and theorems related to them. Discover how encryption algorithms rely on large integers and techniques to handle them effectively, along with primality testing theorems and time comple
0 views • 50 slides
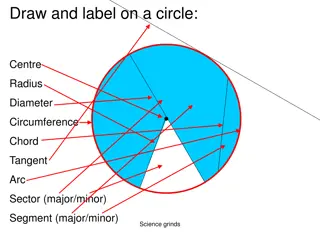
Exploring Circle Concepts and Theorems
Dive into the world of circles with this comprehensive guide covering important terms like center, radius, circumference, and theorems such as double angle, semicircle, and cyclic quadrilateral. Learn about isosceles triangles, tangent properties, chord relationships, and more through visual example
1 views • 21 slides
Exploring Discrete Mathematics through Graph Theory
Delve into the world of discrete mathematics with a focus on graph theory. Learn about graphs, their properties, and essential theorems. Discover how graphs model relations in various applications like network routing, GPS guidance, and chemical reaction simulations. Explore graph terminology, theor
0 views • 26 slides
An Lp Theory for Outer Measures: Application to Singular Integrals II
This discussion covers various topics such as tents (or Carleson boxes), outer measures on the open upper half-plane, sizes of functions on tents, outer essential supremum on subsets, outer Lp spaces, embedding theorems, and estimates related to Linfity-Sinfty and weak L1-Sinfty. The content delves
0 views • 34 slides
Introduction to Analysis Methods of Proof
This content introduces various methods of proof in analysis, including direct proof, counterexamples, and indirect proofs like contrapositive. It covers common notations, sets, symbols, implications, theorems, and examples with analyses. The goal is to understand how to prove or disprove theorems u
0 views • 22 slides
Understanding Circle Theorems and Pythagoras Theorem in Geometry
Explore the key concepts of circle theorems and Pythagoras theorem in geometry. Learn about the parts of a circle, properties of chords, the relationship between the radius and tangent, and how Pythagoras theorem can be applied to solve circle-related problems like finding distances and lengths. Eng
0 views • 8 slides
Circle Theorems Investigation
Explore and understand circle theorems by investigating angles on the same arc from a chord, angle at the centre, and how it relates to the angle at the arc. Follow step-by-step visual instructions to compare angles, cut them out, and discover the relationship between angles in circles.
0 views • 16 slides
Properties and Theorems of Rhombuses, Rectangles, and Squares
Explore the properties and theorems related to rhombuses, rectangles, and squares in geometry. Discover how diagonals behave in rhombuses and rectangles, understand angle measures, and calculate diagonal lengths in rectangles. Enhance your knowledge of special parallelograms with engaging problem-so
0 views • 10 slides
Geometric Postulates and Theorems Relating Points, Lines, and Planes
This section introduces the postulates and theorems related to points, lines, and planes in geometry. It covers basic assumptions, postulates about lines and planes, and theorems about intersections. The concept of "exactly one" and "one and only one" is emphasized, highlighting the unique relations
0 views • 10 slides
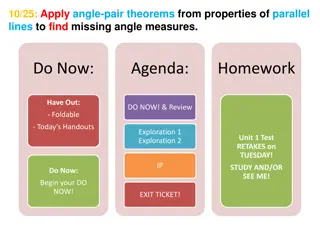
Understanding Angle Pair Theorems in Geometry
Explore the application of angle-pair theorems in finding missing angle measures using properties of parallel lines. Learn about different types of angle pairs such as vertical angles, corresponding angles, same-side interior angles, alternate exterior angles, and more through engaging activities an
0 views • 14 slides
Exploring Metamath: A Computer Language for Mathematical Proofs
Metamath is a computer language designed for representing mathematical proofs. With several verifiers and proof assistants, it aims to formalize modern mathematics using a simple foundation. The Metamath-100 project is focused on proving a list of 100 theorems, with significant progress made in prov
0 views • 17 slides
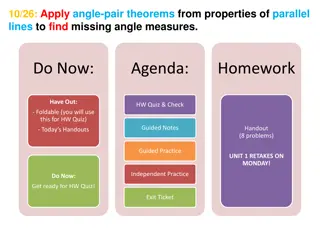
Understanding Angle Pair Theorems in Geometry
Learn how to apply angle pair theorems using properties of parallel lines to find missing angle measures. Explore concepts like corresponding angles, alternate interior angles, alternate exterior angles, and consecutive interior angles through visual aids and practice problems.
0 views • 14 slides
Understanding Polygon Angle-Sum Theorems
Explore the Polygon Angle-Sum Theorems that determine the sum of interior angle measures in polygons. Learn about the Polygon Angle-Sum Theorem, number of sides in polygons, finding angle sums, and the corollary for regular polygons. Practice using the theorems to calculate interior angle measures i
0 views • 18 slides
Understanding Polygon Angles and Theorems
Explore the angles of polygons, including interior and exterior angle sums, theorems 3-13 and 3-14, properties of regular polygons, and measurements of angles in various polygon types. Discover the relationships between sides, vertices, and angles to deepen your geometric knowledge.
0 views • 18 slides
Geometry Fundamentals: Theorems and Concepts Explained
Explore essential concepts in geometry such as solving equations, perpendicular transversal theorem, triangle exterior angle theorem, angle sum theorems, polygon classification, and naming polygorgons. Learn about the interior and exterior angles of triangles and why they add up to specific measurem
0 views • 21 slides
Understanding Digital Electronics Fundamentals with Prof. Dr. Ehssan Al-Bermany
Explore the basics of digital electronics with lectures on NOR gates, exclusive-OR gates, negative AND gates, and more. Understand how these circuits are equivalent to NOR and NAND gates. Discover key theorems of Boolean algebra through De Morgan's theorems. Prepare for a deep dive into Boolean alge
0 views • 26 slides
Understanding Logic Gates and DeMorgan's Theorems in Computer Systems
Exploring the concepts of logic gates, truth tables, and DeMorgan's Theorems in computer systems. Learn about how Boolean algebra is used to analyze digital gates and circuits, the functions of Negative-AND and Negative-OR gates, and how DeMorgan's First and Second Theorems are applied through truth
0 views • 21 slides
Combinatorics Theorems and Examples with Practical Applications
Explanation of combinatorics theorems, such as the Division Rule and Rearranging with Duplicates, along with practical examples like counting anagrams and organizing pairs. The Pigeonhole Principle is also illustrated, showcasing applications in various scenarios with clear steps and outcomes.
0 views • 17 slides
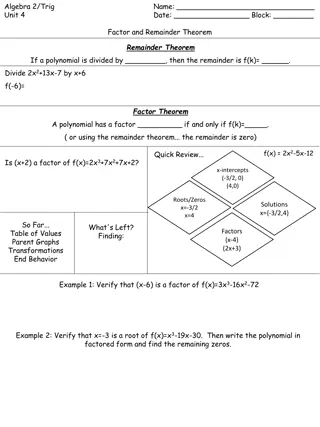
Understanding Polynomial Factor and Remainder Theorems
Exploring the Factor and Remainder Theorems in algebra, including examples on verifying factors, finding roots, applying the Rational Root Test, and determining zeros of polynomials. Learn how to factor polynomials, find remaining zeros, and analyze coefficients to uncover the complete factorization
0 views • 6 slides
Theorems on Convergent Sequences with Proofs and Examples
The lecture covers theorems on convergent sequences, including the convergence of monotonic increasing and decreasing sequences when bounded. Detailed proofs for these theorems are provided, along with examples to determine if a sequence is bounded. The presentation includes step-by-step explanation
0 views • 6 slides
Insights into Cliques and Independent Sets in Graph Theory
Exploring the concepts of cliques, independent sets, and theorems in graph theory regarding enemy relationships, maximum number of edges in 3-free graphs, and properties of multipartite graphs. The propositions and theorems discussed shed light on graph structures and their properties, providing val
0 views • 32 slides