Understanding Angle Pair Theorems in Geometry
Learn how to apply angle pair theorems using properties of parallel lines to find missing angle measures. Explore concepts like corresponding angles, alternate interior angles, alternate exterior angles, and consecutive interior angles through visual aids and practice problems.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
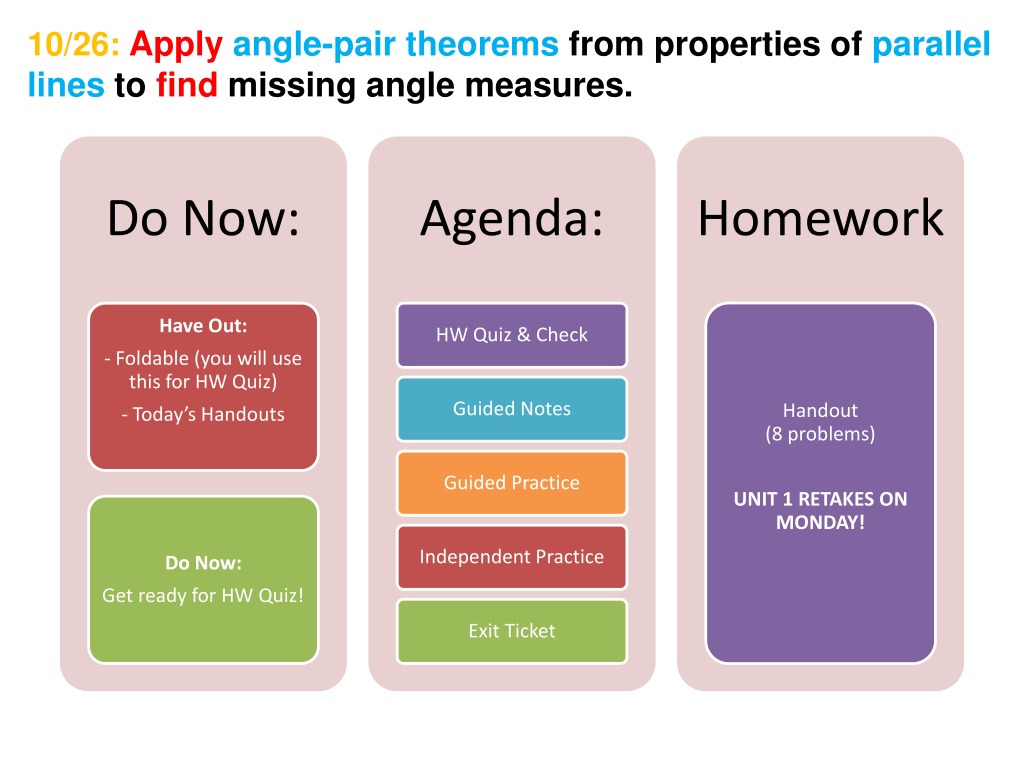
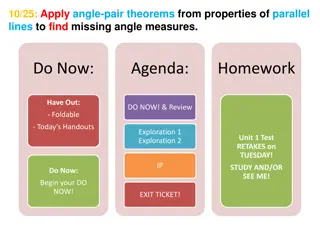
10/26: Apply angle-pair theorems from properties of parallel lines to find missing angle measures. Do Now: Agenda: Homework Have Out: HW Quiz & Check - Foldable (you will use this for HW Quiz) Guided Notes Handout (8 problems) - Today s Handouts Guided Practice UNIT 1 RETAKES ON MONDAY! Independent Practice Do Now: Get ready for HW Quiz! Exit Ticket
We will learn to: - Apply angle-pair theorems from properties of parallel lines to find missing angle measures.
When we are given______________ lines, we can parallel measurements prove relationships about the ____________________ of angle-pairs.
Corresponding Angles Postulate: If two ____parallel____ lines are cut by a ______transversal____, then the ________________ angles are ____________. corresponding congruent parallel Alternate Interior Angles Theorem: If two ________ lines are cut by a _________________, then the __________________ angles are ___________. alternate interior transversal congruent
parallel Alternate Exterior Angles Theorem: If two ________ lines are cut by a ____________, then the ___________________ angles are ___________. alternate exterior transversal congruent parallel Consecutive Interior Angles Theorem: If two ___________ lines are cut by a _____________, then ____________________ angles are ________________. consecutive interior transversal supplementary
1-8: Justify each statement about the diagram. 1. 1 5 Corresponding Angles Postulate 2. 4 and 7 are supplementary Consecutive Interior Angles Theorem 3. 6 7 Vertical Angles 4. 3 6 Alternate Exterior Angles Theorem 5. m 5 + m 7 = 180 Linear Pair 6. 4 5 Alternate Interior Angles Theorem 7. 2 & 5 are supplementary 8. 8 4 Consecutive Interior Angles Theorem Corresponding Angles Postulate
9. If possible, find m1 and m2. Justify both answers. Yes, two lines are parallel There are MANY different strategies to solve. Let s go to the whiteboard!
10. If possible, find m5 and m2 when m1 = 144. Justify both answers. No, two lines are NOT parallel Yes, form a Linear Pair m 1 + m 2 = 180 144 + m 2 = 180 m 2 = 36 Justification: Linear Pair
11. Use the figure on the right to answer the following. Name the angle-pair created by QST and PST: __________________ Linear Pair Identify the measurement relationship: ______________________________ Supplementary Write and solve an equation for x. m QST + m PST = 180
11. Use the figure on the right to answer the following. Write and solve an equation for x. m QST + m PST = 180 (3x + 5) + (6x 14) = 180 9x 9 = 180 9x = 189 x = 21 Justification: Linear Pair 3(21) + 5 + 6(21) 14 = 180 63 + 5 + 126 14 = 180 Check: 180 = 180
11. Use the figure on the right to answer the following. Name the angle-pair created by RPS and TSP: _________________________________ Consecutive Interior Angles Identify the measurement relationship: ______________________________ Supplementary Write and solve an equation for y. m RPS + m TSP = 180
11. Use the figure on the right to answer the following. Write and solve an equation for y. m RPS + m TSP = 180 (y + 8) + 126 = 180 y + 134 = 180 y = 46 Justification: Consecutive Interior Angles Theorem Check: (46) + 8 + 126 = 180 180 = 180
12. If m1 = (6z) and m4 = (4z+ 7), find the value of z and justify, if possible. Yes, the two lines are || Alternate Interior Angles Congruent m 1 m 4 _______ = _______ 6z = 4z + 7 2z = 7 z = 3.5 Justification: Alternate Interior Angles Theorem
Independent Practice Answers 1. m 4 = 115 (Vertical Angles) x = 80 (Consecutive Interior Angles Theorem) 2. Not possible lines are not parallel 3. m 1 = 90 (Consecutive Interior Angles Theorem) m 3 = 65 (Linear Pair with 115 ) m 2 = 65 (Corresponding Angles with 115 ) 4. a) m 2 = 115 (Corresponding Angles with 115 ) b) m 1 = 115 (Alternate Interior Angles with 115 ) 5. x = 12 (Consecutive Interior Angles) y = 10 (Consecutive Interior Angles)