Comprehensive Mathematics Prior Learning Overview
This comprehensive overview delves into key mathematical concepts, including geometry, equations, quadratics, and circle theorems. It covers topics such as similarity, congruence, vectors, and algebraic manipulation, preparing students for more complex problem-solving and geometric proofs. The content highlights the importance of understanding ratios, scale factors, metric conversions, and the application of geometric theorems. Students are guided through enhancing their skills in solving equations, graphing functions, and utilizing vector notation, setting a solid foundation for advanced mathematical studies.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
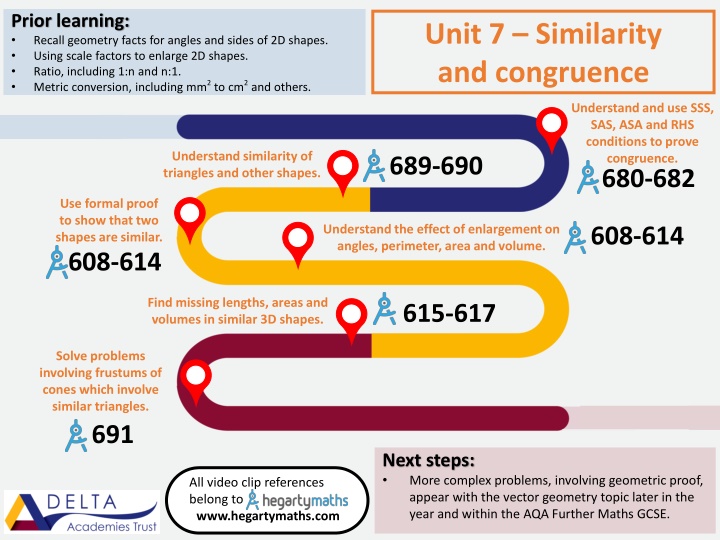
Prior learning: Recall geometry facts for angles and sides of 2D shapes. Using scale factors to enlarge 2D shapes. Ratio, including 1:n and n:1. Metric conversion, including mm2 to cm2 and others. Unit 7 Similarity and congruence Understand and use SSS, SAS, ASA and RHS conditions to prove congruence. 680-682 Understand similarity of triangles and other shapes. 689-690 Use formal proof to show that two shapes are similar. 608-614 Understand the effect of enlargement on angles, perimeter, area and volume. 608-614 Find missing lengths, areas and volumes in similar 3D shapes. 615-617 Solve problems involving frustums of cones which involve similar triangles. 691 Next steps: More complex problems, involving geometric proof, appear with the vector geometry topic later in the year and within the AQA Further Maths GCSE. All video clip references belong to www.hegartymaths.com
Prior learning: Confidence in solving equations. Drawing linear graphs using a table of results or recognising gradient and y-intercept. Unit 8 - Quadratics Sketching and understanding key points on a quadratic graph. 252-257 Expanding trinomials (triple brackets). 166 Sketch graphs of linear, quadratic and cubic functions. 259,299 Solve simultaneous equations graphically. 259 Solve quadratic inequalities. 277 Use iteration to find approximate solutions to equations. 322 Next steps: Within AQA Further Maths GCSE you will be introduced to polynomial division and within A Level Maths you will solve cubic equations algebraically. All video clip references belong to www.hegartymaths.com
Prior learning: Recall angle facts and circle properties. Secure understanding of circle terminology. Drawing circles using a compass. Unit 9 - Circle theorems and geometry Prove and use the circle theorems. 594-606 Understand a tangent is perpendicular to the radius where it meets the circle. 594-602 Find and give reasons for missing angles using multiple circle theorems. 593 Draw graphs based on circles and perpendiculars. 594-602 Find the equation of a tangent to a circle. 320 Recognise and construct a circle on a coordinate grid. 314 Next steps: Within AQA Further Maths GCSE and A Level Maths you will use the general circle equation: All video clip references belong to www.hegartymaths.com (x a)2 + (y b)2 = r2
Prior learning: Using column vectors for translations. Secure understanding of algebraic rules. Applying Pythagoras theorem. Unit 10 - Vector geometry Understand and use vector notation. 622-627 625-626 Represent vectors pictorially. Calculate the sum and difference of two vectors. 625-627 Calculate the length of a vector using Pythagoras theorem. Solve geometric problems using ratio and vectors. 628-636 Produce geometric proof to prove lines are co-linear and parallel. 628-636 Next steps: Vectors are seen within Physics, especially when considering forces (Newtons) and their magnitudes. All video clip references belong to www.hegartymaths.com
Prior learning: Forming and solving linear and quadratics equations, fractions, square numbers Unit 1 - Rearranging with variables on both sides, Algebraic fractions, Surds - Rationalising Denominators, Proof and Functions Rationalise the denominator involving surds 118-119 Multiply and divide algebraic fractions 229 Simplify algebraic fractions Solve quadratic equations from algebraic fractions 244 170 Complex changing the subject of a formula with algebraic fractions 283 Proof and show that questions. 325-326 Complex changing the subject of a formula 285 - 286 Find variations of a function 292-293 Function notation 288 -291 Find the inverse of a linear function 295-296 Find functions of a function. 293-294 & 298 Next steps: Further algebraic manipulation. All video clip references belong to www.hegartymaths.com
Prior learning: Sketching linear and quadratic graphs, algebraic fractions, recipes, ratios and proportion Unit 2 - Reciprocal and exponential graphs Gradient and area under graphs Direct and inverse proportion Recognise, sketch and interpret reciprocal graphs 300-301 Recognise, sketch and interpret exponential functions 302 Sketch an asymptote Solve growth and decay problems 292 Complex changing the subject of a formula with algebraic fractions 283 Proof and show that questions. 325-326 Transformations of graphs to linear, quadratic and cubic functions 307 - 312 Interpret the gradient of a linear or non-linear graph Estimate the area under a graph 319 Recognise and interpret graphs showing direct and indirect proportion 348 Set up and use equations for indirect proportion Set up and use equations for direct proportion 346-347 343-345 Next steps: Trapezium rule, calculus and more proof All video clip references belong to www.hegartymaths.com