Geometry Fundamentals: Theorems and Concepts Explained
Explore essential concepts in geometry such as solving equations, perpendicular transversal theorem, triangle exterior angle theorem, angle sum theorems, polygon classification, and naming polygorgons. Learn about the interior and exterior angles of triangles and why they add up to specific measurements.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
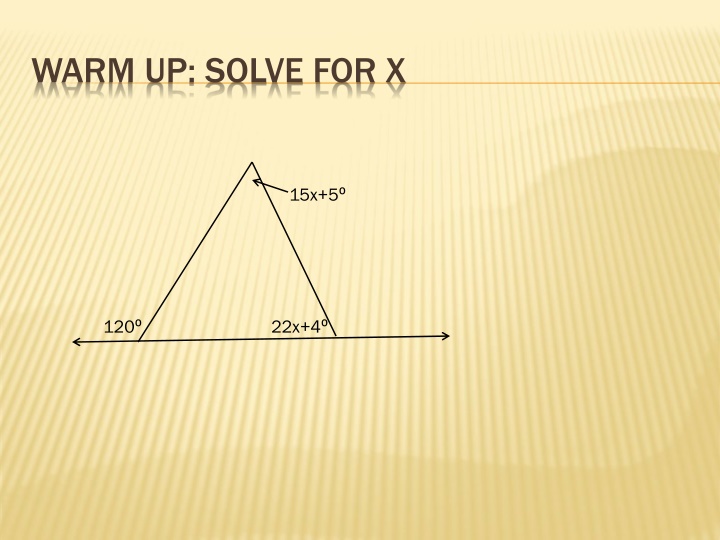
WARM UP: SOLVE FOR X 15x+5 120 22x+4
PERPENDICULAR TRANSVERSAL THEOREM If two lines are parallel and a transversal is perpendicular to one line, then it is perpendicular to the other. Reason: Corresponding angles are congruent
TRIANGLE EXTERIOR ANGLE THEOREM The exterior angle of a triangle equals the sum of the 2 remote interior angles. a=m+h Why??? h a m
PROOF: Prove: m+h=a h Triangle angle sum theorem m+h+g=180 g+a=180 g=180-a m+h+(180-a)=180 m+h-a=0 m+h=a g a m Defn. of supplementary Subtraction property Substitution Subtraction property Addition property
Fill in a missing angle in the picture. P R T L U A 48 42 O J 62 C B K
TRIANGLE INTERIOR ANGLE SUM THEOREM (PROOF BOOK). PROVE THAT THE INTERIOR ANGLES IN A TRIANGLE HAVE A MEASURE SUM OF 180. Construct segment PA so that it is parallel to segment QZ Statements Reasons p z q
3.5 The Polygon Angle-Sum Theorem LEQ: HOW DO WE CLASSIFY POLYGONS AND FIND THEIR ANGLE MEASURE SUMS?
WHAT IS A POLYGON? a closed plane figure with at least three sides that are segments. Sides intersect only at their endpoints and no adjacent sides are collinear.
NAMING POLYGONS Name like naming planes (go in order clockwise or counterclockwise) Vertices are the letters at the points Sides are segments that form the polygon D H K B G M
TWO MAIN TYPES OF POLYGONS Convex Concave has no diagonal with points outside the polygon has at least one diagonal with points outside the polygon
CLASSIFY WHICH ARE CONCAVE AND WHICH ARE CONVEX convex convex Concave Concave Convex Concave Convex
CLASSIFYING BY SIDES 3 sides: 8 sides: Triangle Octagon 4 sides: 9 sides: Quadrilateral Nonagon 5 sides: 10 sides: Pentagon Decagon 6 sides: 11 sides: Undecagon Hexagon 7 sides: 12 sides: Heptagon Dodecagon
HWK: FINISH RIDDLE WKST (BACK) AND COPY TRIANGLE EXTERIOR ANGLE THM & VERTICAL ANGLES THM INTO PROOF BOOK
INTERIOR ANGLES The angles inside a polygon. There is a special rule to find the sum of the interior angle measures. Can you figure it out? Get with a partner Pg. 159 Activity (top) Do all 8 sides (skip the quadrilateral portion) Diagonals cannot overlap or cross each other; connect only vertices
Polygon Polygon Number of Sides Number of Sides Number Number of Triangles of Triangles Formed Formed Sum of interior Sum of interior angle measures angle measures
POLYGON INTERIOR ANGLE-SUM THEOREM The sum of the measures of the interior angles of an n- gon is (n-2)180. Ex.) Sum of angles in a triangle. Tri=3 sides (3-2)180=180 Ex.) Sum of the angles in a quadrilateral (4 sides). (4-2)180=360 Ex.) The sum of the interior angles in a 23-gon
SO WHY DOES IT WORK?? 180(n-2) n=number of sides 6 triangles, so 6(180) degrees but we want 4(180). What s going on?? According to the theorem, the interior angles should sum to 720 degrees. Why?
Polygon Exterior Angle-Sum Theorem The sum of the measures of the exterior angles of a polygon, one at each vertex, is 360.
PROOF OF EXTERIOR ANGLE-SUM What do you know about exterior angles?
IN PROOF BOOK: UNDER POLYGON EXTERIOR ANGLE SUM THM: Prove that the sum of the exterior angles of an n- gon is always 360. In an n-sided polygon, there are n vertices. Thus, we can construct n lines from each vertice. The sum of the measures of these is 180n because of n lines each 180 degrees in measure. The sum of the interior angles is 180(n-2) by the interior angle sum theorem. To calculate the sum of the exterior angles, we subtract the interior sum from the total measure of all angles. Thus we have 180n-(180(n-2)). Statements Reasons
CLASS/HOMEWORK : p. 161-162: 1-25, 47-49, 56