Understanding Polynomial Factor and Remainder Theorems

Exploring the Factor and Remainder Theorems in algebra, including examples on verifying factors, finding roots, applying the Rational Root Test, and determining zeros of polynomials. Learn how to factor polynomials, find remaining zeros, and analyze coefficients to uncover the complete factorization. Discover methods to determine possible roots using Rational Root Test and confirm results using graphing calculators.

• Polynomial
• Factor Theorem
• Remainder Theorem
• Rational Root Test
• Algebra

steinmann_m Follow

Uploaded on Oct 08, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

Presentation Transcript

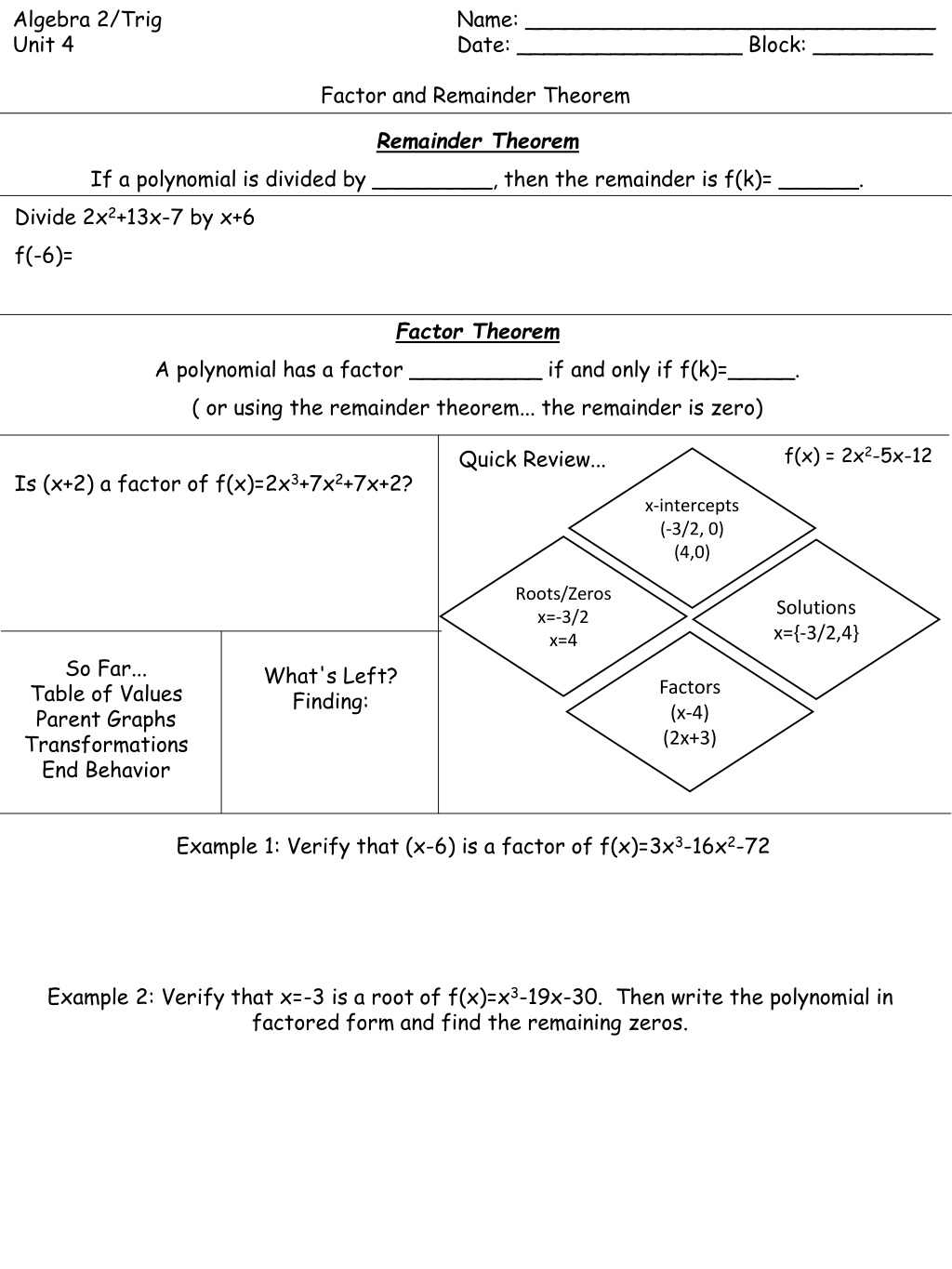
1. Algebra 2/Trig Unit 4 Name: _______________________________ Date: _________________ Block: _________ Factor and Remainder Theorem Remainder Theorem If a polynomial is divided by _________, then the remainder is f(k)= ______. Divide 2x2+13x-7 by x+6 f(-6)= Factor Theorem A polynomial has a factor __________ if and only if f(k)=_____. ( or using the remainder theorem... the remainder is zero) f(x) = 2x2-5x-12 Quick Review... Is (x+2) a factor of f(x)=2x3+7x2+7x+2? x-intercepts (-3/2, 0) (4,0) Roots/Zeros x=-3/2 x=4 Solutions x={-3/2,4} So Far... Table of Values Parent Graphs Transformations End Behavior What's Left? Finding: Factors (x-4) (2x+3) Example 1: Verify that (x-6) is a factor of f(x)=3x3-16x2-72 Example 2: Verify that x=-3 is a root of f(x)=x3-19x-30. Then write the polynomial in factored form and find the remaining zeros.

2. Given one zero of the polynomial, write the polynomial in factored form and find the remaining zeros. 1) f(x)=x3-8x2+4x+48, x=4 2) f(x)=2x3+x2-5x+2, x=-2 Create a polynomial of least degree with zeros at:. 3) x = 3, x = 7, x = -1 4) x = -4, x = 6, x = 2i, x = -2i How many roots does f(x)=2x4+3x3-4x2-3x+2 have? Show that 1 is a root of this function. Find the other roots of this function. When the polynomial is more than degree _____, we need some help finding the roots.

3. Rational Root Test This test allows you to find all POSSIBLE rational roots Rational numbers that can be written as fractions You then need to determine which ones are actually roots. Rational Zero Test: If a polynomial f(x) has integer coefficients, every rational zero of f has the form ? ?= ??????? ?? ? ? ??????? ???????????(??) ??????? ?? ? ? ???????? ???? (?0) where p and q have no common factors other than 1. Step 1: _______________________________________________________ Step 2: _______________________________________________________ Step 3: ________________________________________________________ Step 4: ________________________________________________________ Step 5: ________________________________________________________ Example 1: Find all the rational zeros of f(x) = 2x4 + 3x3 4x2 3x + 2 Example 2: Find all the rational zeros of f(x) = x3 + 3x2 x 3

4. Example 3: Find all the rational zeros of f(x) = x4 - x3 + x2 3x - 6 Example 4: Find all the rational zeros of g(x) = 2x3 + 3x2 8x + 3 You Try: Find all the rational zeros of g(x) = x3 + 2x2 11x - 12 Putting it all Together In the next examples we will: a) Find all possible roots using Rational Root Test (RRT) b) Find all the roots c) List the Complete Factorization d) Identify all Zeros e) Confirm our results using a graphing calculator

5. In the next examples we will: a) Find all possible roots using RRT b) Find all the roots c) List the Complete Factorization d) Identify all Zeros e) Confirm our results using a graphing calculator f) GRAPH!!! f(x) = x4-3x3-11x2+3x+10 x-intercepts: (__,0), (__,0), (__,0), (__,0) y-intercepts: (0,__) As x->- , f(x) ->___ As x-> , f(x) ->___ In the next examples we will: a) Find all possible roots using RRT b) Find all the roots c) List the Complete Factorization d) Identify all Zeros e) Confirm our results using a graphing calculator f) GRAPH!!! f(x)=2x4+7x3-4x2-27x-18 x-intercepts: (__,0), (__,0), (__,0), (__,0) y-intercepts: (0,__) As x->- , f(x) ->___ As x-> , f(x) ->___

6. f(x)=2x4+7x3-4x2-27x-18 x-intercepts: (__,0), (__,0), (__,0), (__,0) y-intercepts: (0,__) As x->- , f(x) ->___ As x-> , f(x) ->___ f(x)=2x4+7x3-4x2-27x-18 x-intercepts: (__,0), (__,0), (__,0), (__,0) y-intercepts: (0,__) As x->- , f(x) ->___ As x-> , f(x) ->___