Circle Theorems Investigation
Angle at Centre, Angle on Arc
Investigation
Mark a point on the circle below then
join it to both ends of the chord.
Mark a point on the circle below then
join it to both ends of the chord.
Mark another point and repeat the
process.
Mark another point and repeat the
process.
Shade in both angles just created on
the circle.
Shade in both angles just created on
the circle.
Cut out the angles and compare them
to each other.
Compare them with others of the
same colour card.
Now join the centre of the circle to
both ends of the chord.
Cut out the angles and compare them
to each other.
Compare them with others of the
same colour card.
Now join the centre of the circle to
both ends of the chord.
Shade in the angle then cut it out.
Will the two smaller angles fit in the
remaining gap?
Shade in the angle then cut it out.
This demonstrates two circle theorems.
Angles on the same arc from a
chord are equal.
Angle at the centre is twice the
angle at the arc when drawn from
the same chord.
The general case
The general case
The general case
The general case
The general case
Note to Teacher
•
Use different coloured card for each
lettered resource - this will make it
easier for the pupils to compare results.
Explore and understand circle theorems by investigating angles on the same arc from a chord, angle at the centre, and how it relates to the angle at the arc. Follow step-by-step visual instructions to compare angles, cut them out, and discover the relationship between angles in circles.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
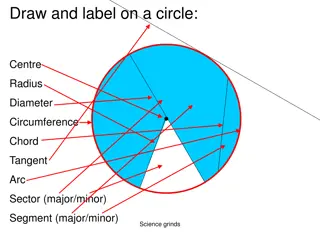
Angle at Centre, Angle on Arc Investigation
Mark a point on the circle below then join it to both ends of the chord.
Mark another point and repeat the Mark a point on the circle below then join it to both ends of the chord. process.
Mark another point and repeat the process. the circle. Shade in both angles just created on
Cut out the angles and compare them to each other. Shade in both angles just created on the circle. Compare them with others of the same colour card.
Cut out the angles and compare them to each other. Compare them with others of the same colour card. Now join the centre of the circle to both ends of the chord.
Now join the centre of the circle to both ends of the chord. Shade in the angle then cut it out.
Will the two smaller angles fit in the remaining gap? Shade in the angle then cut it out.
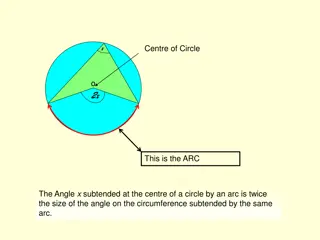
This demonstrates two circle theorems. Angles on the same arc from a chord are equal. Angle at the centre is twice the angle at the arc when drawn from the same chord.
The general case ? ? ? ?? ?? ? ?
The general case ? + ? ? ? ? + ?
Note to Teacher Use different coloured card for each lettered resource - this will make it easier for the pupils to compare results.
