Understanding Circle Theorems and Pythagoras Theorem in Geometry
Explore the key concepts of circle theorems and Pythagoras theorem in geometry. Learn about the parts of a circle, properties of chords, the relationship between the radius and tangent, and how Pythagoras theorem can be applied to solve circle-related problems like finding distances and lengths. Engage with visual representations and step-by-step solutions to enhance your understanding and problem-solving skills in geometry.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
24 September 2024 Circle theorems using Pythagoras theorem LO: To use Pythagoras theorem to solve problems from circles. www.mathssupport.org
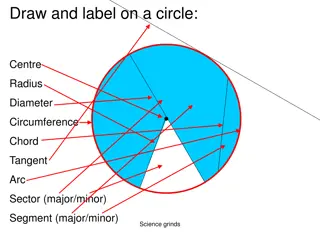
Naming the parts of a circle A circle is a set of points equidistant from a fixed point called the centre. The distance around the entire circle boundary is called the circumference. The radius is any line segment joining its centre to any point on the circumference. radius centre The diameter is a line segment passing through the centre. Note that the diameter of a circle is twice its radius circumference www.mathssupport.org
Naming the parts of a circle A chord is any line segment that joins two points on the circle. Therefore, a diameter is an example of a chord. It is the longest possible chord. The line that touches the circumference in exactly one point is called a tangent or a tangent line. The point where the tangent touches the circle is called the point of contact or point of tangency. centre www.mathssupport.org
The chord of a circle Draw a circle, label the centre O Choose any point on the circumference and label it A Draw any chord from A, Label B the other point on the circumference. Construct the perpendicular from O to AB which cuts the chord at M, B O Measure the lengths of AM and BM, M What do you notice? Repeat the procedure with another circle and chord A AM = BM Statement The perpendicular from the centre of a circle to a chord bisects the chord www.mathssupport.org
The chord of a circle A circle has a chord of length 12 cm. If the radius of the circle is 8 cm, find the shortest distance from the centre of the circle to the chord. Solution: The shortest distance is the perpendicular distance. The line drawn from the centre of a circle, perpendicular to a chord, bisects the chord, so BM = MA = 6 cm Using Pythagoras theorem 82= 62+ x2 64 - 36 = x2 B 8 cm 6 cm 28 = x2 O x M 6 cm 2 7 = x A The length OM is approximately 5.29cm www.mathssupport.org
Radius-tangent Draw a circle, label the centre O Choose any point on the circumference and label it A Draw at A, as accurately as possible, a tangent TA Draw the radius OA. Measure the angle OAT with a protractor, What do you notice? Repeat the procedure with another circle and tangent O AT = 90o O T A Statement The tangent to a circle is perpendicular to the radius at the point of contact. www.mathssupport.org
Radius-tangent Find the length AB if the radius is 6, AB is tangent at A and OB is double the length of the radius. Solution: As OA is the radius, A is the point of tangency and AB is a tangent The angle OAB is 90o so, the triangle OAB is a right angled triangle Using Pythagoras theorem 122 = 62 + AB2 O 144 = 36 + AB2 12 cm 144 - 36 = AB2 6 cm 108 = AB2 B A 10.4 = AB The length AB is 10.4cm www.mathssupport.org
Thank you for using resources from A close up of a cage Description automatically generated For more resources visit our website https://www.mathssupport.org If you have a special request, drop us an email info@mathssupport.org Get 20% off in your next purchase from our website, just use this code when checkout: MSUPPORT_20 www.mathssupport.org