Geometry Investigations and Theorems
Starter
Find the missing angles and give reasons.
50
Supplementary
angles sum to
180°
113
Corresponding
angles are equal
121
Alternate
angles are equal
Centre
Radius
Diameter
Arc
Tangent
Sector
Major segment
Minor segment
Circumference
Label the diagrams using the key words:
Chord
Circle Theorems
1) Draw a line from the centre of
your circle to a point on the
circumference.
2) Draw the tangent at that point.
3) Measure the angle between the
radius and the tangent.
What can you tell me?
Investigation
A tangent is perpendicular to a radius.
Theorem
1) Draw two lines from the centre to
the circumference.
3) Draw two more lines to the other
side of your circle from the same points
that you drew the first two lines.
What do you notice?
Investigation
The angle at the centre is
twice the angle at the
circumference.
Theorem
Proof
x°
y°
= (180 – x)/2
= (180 – y)/2
= 180 – (½x + ½y)
= 360 – (x + y)
∴
t
he angle at the centre is twice
the angle at the circumference.
1) Draw the circle’s diameter.
2) Draw two lines to a point at the
circumference.
3) Measure the subtended angle of the
diameter from the circumference.
What do you notice?
Investigation
The angle in a semi-circle is 90
o.
Theorem
Proof
Using “the angle at the
centre is twice the angle at
the circumference” means
that
= 180
°
as it is a
straight line.
= ½
= ½ x 180
°
= 90
°
∴
t
he angle in a semi-circle is 90
o.
a
b
c
d
1) On your circle pick 4 points
a,b,c,d
.
Don’t pick points directly opposite each
other.
2) Connect points
a
and
b
to
c
.
3) Connect points
a
and
b
to
d.
4) Measure the angles subtended from
a
and
b
at
c
and
d.
What do you notice?
Investigation
a
b
c
d
Angles subtended by the
same arc are equal.
Theorem
Proof
x°
Using “the angle at the
centre is twice the angle at
the circumference” means
that
2x°
= 2
y°
= 2
2y°
2x = 2y
∴
x = y
∴
a
ngles subtended by the
same arc are equal.
1) Draw a quadrilateral inside your
circle. Every vertex must be
touching the circumference of the
circle.
2) Measure the angles inside the
quadrilateral.
What can you tell me?
(Of course they add up to 360; it’s a
quadrilateral!)
Investigation
Opposite angles in a cyclic
quadrilateral sum to 180
o.
Theorem
Proof
Using “the angle at the
centre is twice the angle at
the circumference” means
that
x°
y°
= 2
= 2
2x + 2y = 360º
2(x + y) = 360º
x + y = 180º
∴
opposite angles in a cyclic quadrilateral
sum to 180
o.
1) Draw a triangle inside your circle
with all vertices on the
circumference.
2) Draw a tangent at one of the
vertices.
3) Measure the angles between the
tangent and the triangle, and the
angles of the triangle.
What can you tell me?
Investigation
Angles in alternate segments are equal.
Theorem
Proof
x°
90-x
x°
For cases when the chord isn’t a
diameter?
Using “
angles subtended by the same arc are equal”
∴
angles in alternate segments are equal.
1) Draw two tangents from your
circle that meet at a point.
2) Measure the lengths of these
tangents.
What can you tell me?
Investigation
Tangents from a point are equal.
Theorem
Proof
r
r
x
Using Pythagoras’ Theorem
∴
tangents
from a point
are equal.
Show me a problem that can be
solved using:
•
Angle at the centre rule.
•
Angles subtended from an arc.
•
Angles subtended from the
diameter.
•
Opposite angles in a cyclic
quadrilateral.
Circle Theorems
Circle Theorems
Answers
1)
67º because angles subtended by the same arc are equal.
2)
56º because the angle at the centre is twice that at the circumference.
3)
69º because the angle in a semi-circle is 90º.
4)
37º because the radii make an isosceles triangle.
5)
109º because the radii make an isosceles triangle.
6)
44º because angles subtended by the same arc are equal.
7)
111º because opposite angles in a cyclic quadrilateral sum to 180º.
8)
90º because the tangent and the radius are perpendicular.
9)
29º because angles in alternate segments are equal.
10)
67º because opposite angles in a cyclic quadrilateral sum to 180º.
11)
90º because the tangent and the radius are perpendicular.
12)
27º because angles in alternate segments are equal.
Explore various circle theorems and investigations involving angles, tangents, radii, and circumferences. Discover the relationships between angles at the center and circumference, the properties of tangents, and the angle measurements within a circle. Engage in investigations to understand the significance of different points and lines on a circle.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
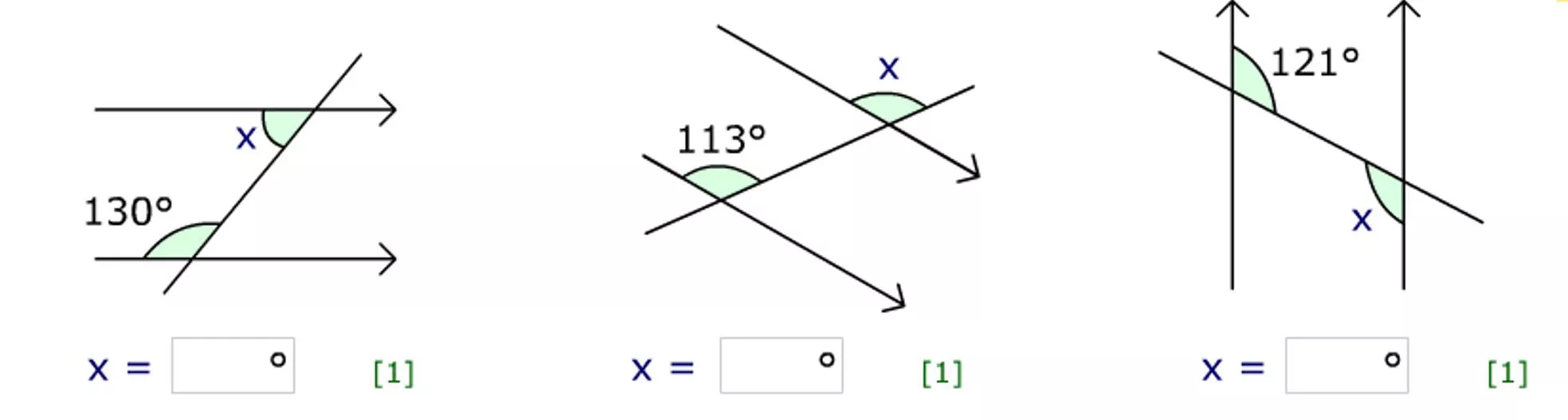
Starter Find the missing angles and give reasons. 50 113 121 Supplementary angles sum to 180 Corresponding angles are equal Alternate angles are equal
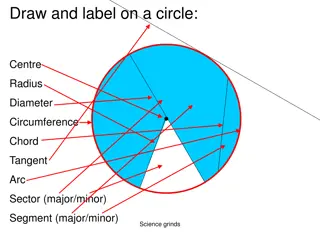
Circle Theorems Label the diagrams using the key words: Radius Diameter Centre Chord Minor segment Circumference Arc Major segment Sector Tangent
Investigation 1) Draw a line from the centre of your circle to a point on the circumference. 2) Draw the tangent at that point. 3) Measure the angle between the radius and the tangent. What can you tell me?
Theorem A tangent is perpendicular to a radius.
Investigation 1) Draw two lines from the centre to the circumference. 3) Draw two more lines to the other side of your circle from the same points that you drew the first two lines. What do you notice?
Theorem The angle at the centre is twice the angle at the circumference.
Proof = (180 x)/2 = (180 y)/2 x y = 180 ( x + y) = 360 (x + y) the angle at the centre is twice the angle at the circumference.
Investigation 1) Draw the circle s diameter. 2) Draw two lines to a point at the circumference. 3) Measure the subtended angle of the diameter from the circumference. What do you notice?
Theorem The angle in a semi-circle is 90o.
Proof = 180 as it is a straight line. Using the angle at the centre is twice the angle at the circumference means that = = x 180 = 90 the angle in a semi-circle is 90o.
Investigation d 1) On your circle pick 4 points a,b,c,d. Don t pick points directly opposite each other. 2) Connect points a and b to c. 3) Connect points a and b to d. 4) Measure the angles subtended from a and b at c and d. c b a What do you notice?
Theorem d c Angles subtended by the same arc are equal. b a
Proof Using the angle at the centre is twice the angle at the circumference means that = 2 x y = 2 2x 2y 2x = 2y x = y angles subtended by the same arc are equal.
Investigation 1) Draw a quadrilateral inside your circle. Every vertex must be touching the circumference of the circle. 2) Measure the angles inside the quadrilateral. What can you tell me? (Of course they add up to 360; it s a quadrilateral!)
Theorem Opposite angles in a cyclic quadrilateral sum to 180o.
Proof Using the angle at the centre is twice the angle at the circumference means that = 2 x = 2 2x + 2y = 360 2(x + y) = 360 x + y = 180 opposite angles in a cyclic quadrilateral sum to 180o. y
Investigation 1) Draw a triangle inside your circle with all vertices on the circumference. 2) Draw a tangent at one of the vertices. 3) Measure the angles between the tangent and the triangle, and the angles of the triangle. What can you tell me?
Theorem Angles in alternate segments are equal.
Proof For cases when the chord isn t a diameter? x 90-x x Using angles subtended by the same arc are equal angles in alternate segments are equal.
Investigation 1) Draw two tangents from your circle that meet at a point. 2) Measure the lengths of these tangents. What can you tell me?
Theorem Tangents from a point are equal.
Proof Using Pythagoras Theorem r tangents from a point are equal. r x
Show me a problem that can be solved using: Angle at the centre rule. Angles subtended from an arc. Angles subtended from the diameter. Opposite angles in a cyclic quadrilateral.
Answers 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 67 because angles subtended by the same arc are equal. 56 because the angle at the centre is twice that at the circumference. 69 because the angle in a semi-circle is 90 . 37 because the radii make an isosceles triangle. 109 because the radii make an isosceles triangle. 44 because angles subtended by the same arc are equal. 111 because opposite angles in a cyclic quadrilateral sum to 180 . 90 because the tangent and the radius are perpendicular. 29 because angles in alternate segments are equal. 67 because opposite angles in a cyclic quadrilateral sum to 180 . 90 because the tangent and the radius are perpendicular. 27 because angles in alternate segments are equal.
