Understanding Circle Theorems and Equations of Circles
Explore circle theorems and equations of circles in geometry, including concepts like opposite angles in cyclic quadrilaterals, angles on a straight line, and important theorems like the perpendicular bisector of a chord passing through the center of a circle. Learn how to apply these theorems to find equations of tangents, points on circles, and lengths of segments in circle geometry problems.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Circle Theorems & The Equation of a Circle Apply knowledge of Circle Theorems to problems involving the Equation of a Circle
? ?? = 97 Opposite angles in a cyclic quadrilateral add to 180 ? ?? = 83 Angles on a straight line add to 180 ? ? ?? = ? ?? =46 Alternate Segment Theorem ? = 180 46 83 ? = 51 Angles in a triangle add to 180
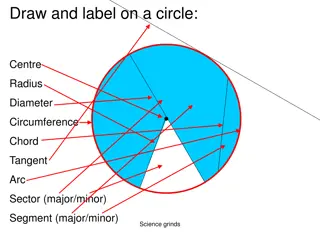
Important Theorems to remember... The perpendicular bisector of any chord passes through the centre of the circle. e.g. Given two points on the circumference of the circle, if the centre of the circle is (3, ?), find ?. Tangent is at right-angles to the radius. What is it? Angle in a semi-circle is ?? (so two top lines are perpendicular) What is it? What is it? e.g. Find equation of the tangent at the point (2,4) Possible exam q? e.g. Use fact lines are perpendicular to find other side of diameter. Possible exam q? Possible exam q?
Your Turn All of these theorems involve perpendicular lines. We ll also need to use the formula for the equation of a line. Gradient of line Gradient of perpendicular line 1 ? 3 3 1 4 ? ? 4 1 2 2 4 3 ? 3 4 If a line has gradient ? and passes through the point ?1,?1 then it has equation: ? ??= ? ? ??
Equation of a Tangent (GCSE) The equation of this circle is ?2+ ?2= 20 ? 4,2 is a point on the circle. Work out the equation of the tangent to the circle at ?, in the form ? = ?? + ? As always, to find an equation we need (i) a point and (ii) the gradient. ? ? Point: (4,2) Gradient? Gradient of radius is ? ?=? ? ? Gradient of tangent = ? ? ? ? = ? ? ? ? = ?? + ??
Your Turn A circle C has centre (3, 1) and passes through the point P(8, 3). (a) Find an equation for C. (b) Find an equation for the tangent to C at P. (a) (b)
Using the Tangent to a Circle The equation of Circle C is ? + 52+ ? 92= 25. A line through the point P (8, 7) is a tangent to the circle C at the point T. Find the length of PT. There are 2 possible values of T and PT1 = PT2 as tangents from an external point are equal in length. ?
Points on the Circumference Two points on the circumference of a circle are (2,0) and (0,4). If the centre of the circle is 6,? , determine ?. Gradient of chord: ? ?= ? Midpoint of chord: (1,2) Gradient of radius =? Equation of radius: ? ? =? ? (6,?) ?? ? 4 If ? = ?: ? ? =? ?? ? ? = ?.? 2
Your Turn Points ?(1,3) and (5,9) form a chord of a circle. If the centre of the circle is at (12,?), find ?. The equation of this circle, centre C, is ? 32+ ? 52= 17 (a) Show working to explain why ?? is a tangent to the circle. (b) Show that the length ?? is equal to the radius of the circle. Midpoint = 3,6 Gradient of AB =6 Gradient of radius = 2 4=3 2 3 Gradient of OP = 1 Gradient of ?? = 1 5 4 3= 4 1 4 4 = 1 line is perpendicular to the radius. Equation of radius: ? 6 = 2 ? 6 = 2 ? = 2 4 3? 3 ? ? 3? + 2 3? + 8 If ? = 12: ? = 2 312 + 8 = 8 + 8 = 0
Exercise 3 Question 2: [AQA Practice Paper] The sketch shows part of a circle, centre C, that intersects the axes at points ?,? and ?. Question 1: [AQA Practice Paper] The sketch show point ? on a circle, centre C. The equation of the tangent at P is ? = 13 2?. (a) Explain why the centre of the circle lies on the line ? = 7 Because (?,?) is the midpoint of ?? and the perpendicular bisector of QR goes through the centre of the circle. (b) Show that the line ? = ? is the perpendicular bisector of the line ??. Midpoint of ??: (2,2). Gradient: ?. Therefore perp bis.: ? ? = ?(? ?) (c) Work out the equation of the circle. Centre: (7,7) Radius: ?? ? ??+ ? ??= ?? ? ? (a) Work out the gradient of PC. ? (b) Work out the equation of the circle. Equation of PC: ? ? =? ? ?,? ??+ ? ??= ?? ? ?? ? ? ? ?
Exercise 3 Question 3: The points ?(3,5) and ? 10,? form a diameter of a circle. The point ? 9,8 is another point on the circle. Question 4: The diagram shows points ? 4,3 ,?(10,5) and ?(12,?). ? is the centre of the circle and ?? form a chord of the circle. ? is the midpoint of ??. (a) Determine the gradient of the line ??. (a) Determine the gradient of ?? and the coordinate of ?. ? =? (b) Hence find the equation of ??. ? ? = ?(? ?) (c) Hence determine the value of ?. ? = ?? ? ? ? ? ?, ?(?,?) ? (b) Hence determine the equation of the line ??. ? ? = ? ? ? (c) Hence, given that the point ? lies on this line, determine the value of ?. (10, 6) ? ? ? (d) Find the equation of the circle. ? ???+ ? + ???= ??? ? ? 9,8 ? ? 10,5 ? 10,? ? ? 3,5 ? 12,? ? 4,3 ?
Exercise 3 Question 5: A line with equation ? = 4? 13 is tangent to a circle at the point ? 5,7 . Question 6: The points ? 3,5 and ? 6,14 lie on the circumference of a circle, and ? is at the top of the circle. Determine: (a) Determine the equation of ??. ? ? = ? (a) The centre of the circle. ?? ? ? ? (?,?) (a) The equation of the circle. (b) Determine the value of ?. ? = ? ? ??+ ? ??= ?? ? ? (c) Hence determine the equation of the circle. ? ??+ ? ??= ?? ? 6,14 ? ? ? 5,7 ? 3,5 ? 9,?