Exploring Circle Concepts and Theorems

Dive into the world of circles with this comprehensive guide covering important terms like center, radius, circumference, and theorems such as double angle, semicircle, and cyclic quadrilateral. Learn about isosceles triangles, tangent properties, chord relationships, and more through visual examples. Understanding these circle principles will enhance your geometry knowledge and problem-solving skills.

• Circle Concepts
• Geometry Theorems
• Visual Examples
• Isosceles Triangles
• Tangent Properties

stransky_g Follow

Uploaded on Sep 15, 2024 | 1 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

Presentation Transcript

1. Draw and label on a circle: Centre Radius Diameter Circumference Chord Tangent Arc Sector (major/minor) Segment (major/minor) Science grinds

2. Circle Fact 1. Isosceles Triangle Any triangle AOB with A & B on the circumference and O at the centre of a circle is isosceles. r a 180 - 2a r a Science grinds

3. Circle Fact 2. Tangent and Radius The tangent to a circle is perpendicular to the radius at the point of contact. Science grinds

4. Circle Fact 3. Two Tangents The triangle produced by two crossing tangents is isosceles. Science grinds

5. Circle Fact 4. Chords If a radius bisects a chord, it does so at right angles, and if a radius cuts a chord at right angles, it bisects it. Science grinds

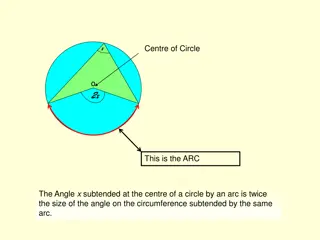
6. Circle Theorem 1: Double Angle The angle subtended by an arc at the centre of a circle is twice the angle subtended at the circumference. Science grinds

7. Circle Theorem 2: Semicircle The angle in a semicircle is a right angle. Science grinds

8. Circle Theorem 3: Segment Angles Angles in the same segment are equal. Science grinds

9. Circle Theorem 4: Cyclic Quadrilateral The sum of the opposite angles of a cyclic quadrilateral is 180o. Science grinds

10. Circle Theorem 5: Alternate Segment The angle between a chord and the tangent at the point of contact is equal to the angle in the alternate segment. Science grinds

11. Circle Theorem 1: Double Angle The angle subtended by an arc at the centre of a circle is twice the angle subtended at the circumference. Proof Science grinds

12. b 180 - 2b 2a + 2b = 2(a + b) b 180 2a a a Science grinds

13. Circle Theorem 2: Semicircle The angle in a semicircle is a right angle. Proof Science grinds

14. b 360 2(a + b) = 180 180 = 2(a + b) 90 = (a + b) 180 2b 180 2a b a a Science grinds

15. Circle Theorem 3: Segment Angles Angles in the same segment are equal. Proof Science grinds

16. a a 2a Science grinds

17. Circle Theorem 4: Cyclic Quadrilateral The sum of the opposite angles of a cyclic quadrilateral is 180o. Proof Science grinds

18. a 2a + 2b = 360 2(a + b) = 360 2b a + b = 180 2a b Science grinds

19. Circle Theorem 5: Alternate Segment The angle between a chord and the tangent at the point of contact is equal to the angle in the alternate segment. Proof Science grinds

20. 90 - a a 180 2(90 a) 2a 180 180 + 2a 90 - a a Science grinds

21. Double Angle Semicircle 1 2 3 Segment Angles 4 5 Cyclic Quadrilateral Alternate Segment Science grinds