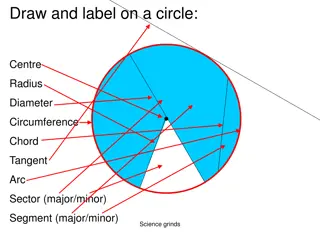
Understanding Circle Geometry Principles
Explore key concepts in circle geometry such as angles subtended at the center and circumference, cyclic quadrilaterals, properties of tangents and chords, and the significance of major and minor segments. Uncover relationships between angles, segments, and points on a circle, including alternate segments and the angle in a semicircle. Enhance your knowledge of circle geometry through illustrations and explanations.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
x Centre of Circle o 2x This is the ARC The Angle x subtended at the centre of a circle by an arc is twice the size of the angle on the circumference subtended by the same arc.
Case2 Centre of Circle x o 2x This is the ARC Angle subtended at the Centre is twice the angle at the circumference
We are ALL EQUAL x x Major Segment x Minor Segment This is the Arc Angles Subtended in the same segment of a circle are equal
A If this angle was 600 then angle BCD would be 1800-600=1200 B o 180-x x D C 1200 Points which lie on the circumference of the same circle are called cyclic (or concyclic) points. A cyclic quadrilateral is a quadrilateral with all its four corners (vertices) on the circumference of the same circle. Cyclic Quadrilateral
B O T A TA=TB Tangents NB Triangles OBT and OAT are CONGRUENT!
E Major Segment D Minor Segment A B C The Shaded Segment BEDis called the alternate segment to the angle CBD The angle between a tangent to a circle and a chord drawn through the point of contact is equal to any angle subtended by the chord at the circumference in the alternate segment
The angle in a semi circle is 90 degrees! Centre of Circle
This powerpoint was kindly donated to www.worldofteaching.com http://www.worldofteaching.com is home to over a thousand powerpoints submitted by teachers. This is a completely free site and requires no registration. Please visit and I hope it will help in your teaching.