Understanding the Parts of a Circle and Calculating Arc Length
A circle's components include its center, radius, diameter, circumference, chords, tangents, and segments. Arcs are parts of the circumference, with minor and major arcs distinguished by their lengths. Sectors are regions enclosed by radii and arcs. Learn about these key concepts and how to calculate arc length using radians.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
24 September 2024 Length of arc LO: To know the formula to calculate the length of an arc and perform calculations if the angle is given in radians. www.mathssupport.org www.mathssupport.org
Naming the parts of a circle A circle is a set of points equidistant from a fixed Naming the parts of a circle point called the centre. The distance around the entire circle boundary is called the circumference. The radius is any line segment joining its centre to any point on the circumference. The diameter is a line segment passing through the centre. Note that the diameter of a circle is twice its radius radius centre circumference Tuesday, 24 September 2024 www.mathssupport.org www.mathssupport.org
Naming the parts of a circle A chord is any line segment that joins two points on the circle. Therefore, a diameter is an example of a chord. It is the longest possible chord. The line that touches the circumference in exactly one point is called a tangent or a tangent line. The point where the tangent touches the circle is called the point of contact or point of tangency. centre Tuesday, 24 September 2024 www.mathssupport.org www.mathssupport.org
Naming the parts of a circle The region of a circle enclosed by a chord and an arc a Segment is called Any chord encloses two segments, which have different areas. If the segment is enclosed by the diameter asemicircle semicircle Major segment semicircle it is called Minor segment Tuesday, 24 September 2024 www.mathssupport.org www.mathssupport.org
Arcs and sectors arc An arc is any continuous part of the circumference. Tuesday, 24 September 2024 www.mathssupport.org www.mathssupport.org
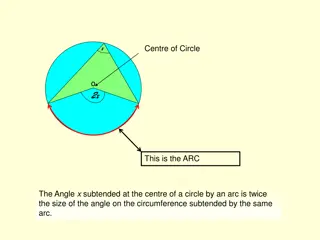
Arcs B Minor arc Minorarc AB is the shortest distance between two points A and B on the circumference of a circle. Major arc AB is the longer distance around the circumference from A to B A Major arc Tuesday, 24 September 2024 www.mathssupport.org www.mathssupport.org
Arcs and sectors When an arc is bounded by two radii a sector is formed. arc A sector is the region enclosed by two radii and an arc. sector Tuesday, 24 September 2024 www.mathssupport.org www.mathssupport.org
Arcs and sectors When an arc is bounded by two radii B a sector is formed. arc Minor A sector is the region enclosed by two radii and an arc. The sector AOC enclosed with the smallest angle is the minor sector. The sector AOC enclosed with the largest angle is the major sector. A sector sector O Major sector Tuesday, 24 September 2024 www.mathssupport.org www.mathssupport.org
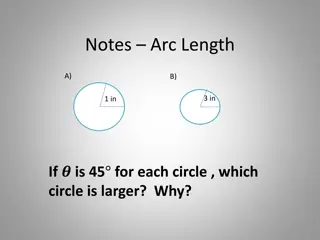
Length of an arc Any central angle in a circle is a fraction of 2 ? ?? So, you can calculate the length of the arc the angle subtends as a fraction of the circumference. ? Arc length = ??? ?? O Arc length = r r B r Where r is the radius and is the central angle measured in radians arc A www.mathssupport.org www.mathssupport.org
Length of an arc Find the arc length AB if the radius of the circumference is 8 cm and the angle is ?? ? B Arc length = r arc ?? ? 8 cm = 8 cm ?? ? r = O ?? ? Arc length = 8 A Arc length = 6 www.mathssupport.org www.mathssupport.org
Area of a sector A circle has radius 2.5 mm. Find the size of a central angle subtended by an arc of length 9 mm. Arc length = r 9 = 2.5 ? ?.? ? = ? = ?.? ??? Another way of writing angles in radians is 3.6c where the c stands for circular measure www.mathssupport.org www.mathssupport.org
Thank you for using resources from A close up of a cage Description automatically generated For more resources visit our website https://www.mathssupport.org If you have a special request, drop us an email info@mathssupport.org www.mathssupport.org www.mathssupport.org