Understanding Circumference and Arc Length in Geometry
Learn about the concepts of circumference and arc length in geometry, including formulas for calculating them, converting between degrees and radians, and solving real-life problems utilizing these concepts. Explore examples to enhance your understanding of these geometric principles.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Lesson 11-1 Circumference and Arc Length
Objectives Use the formula for circumference Use arc length to find measures Solve real-life problems Measure angles in radian
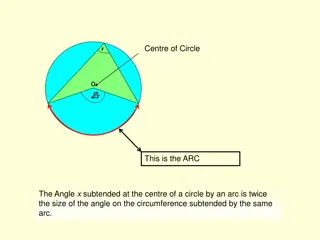
Vocabulary Arc length a portion of the circumference of a circle Circumference the distance (perimeter) around the circle Radian a measure in units of central angles (180 = 1 radian and 360 = 2 radians)
Circumference (Perimeter) The perimeter of a circle is it s circumference. Formula ? = ??? = ?? is on the formula sheet
Arc Length (part of circumference) The portion of the circumference that corresponds to the arc length is determined by the ratio of the central angle to 360
Degrees and Radians Converting back and forth between degrees and radians involves 360 = 2 radians
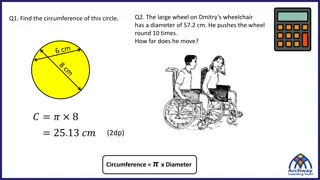
Example 1 Find each indicated measure. a) Circumference of a circle with a radius of 11 inches. b) Radius of a circle with a circumference of 4 millimeters. Answer: a) ? = ??? = ?? ?? = ??? ? ?= ? b) ? = ??? = ? = ???
Example 2a Find each indicated measure. a) Arc length of ?? Answer: ?? =100 2? 12 360 ?? =2400? = 6.66 360
Example 2b Find each indicated measure. b) Circumference of P Answer: ?? = 6.5 =130 360? 2340 130= 18 = ?
Example 2c Find each indicated measure. c) ? ?? Answer: ? ?? ???(?? ??.?? ) = ?? ?? =21(360) 28.64? 84 ?
Example 3 The radius of a wheel on a toy truck is 4 inches. To the nearest foot, how far does the wheel travel when it makes 7 revolutions? ? = ??? = ?? ?? = ? ?? = ??? ??? ?? Answer: 176 ft.
Example 4 A path is built around four congruent circular fields. The radius of each field is 100 feet. How long is the path? Round to the nearest hundred feet. ? ? ? = ? ?? ??? + ? ??? ? = ???? + ??? = ????.?? Answer: P 1400.
Example 5 Answer: a) Convert 30 to radians ?? ???= ? ??(??) ??? ? ?= ? ?? = ? b) Convert ?? ? radians to degrees. ?? ?=??? ??(???) ??? ??? = ? ??.? = ?
Summary & Homework Summary: Circumference of a circle (perimeter), C = 2 r = d Arc length is a proportion of the circumference 180 degrees is radians Homework: none