Understanding Radians: Measurement, Arc Length, Sectors, and Trigonometry Equations
This content covers various topics related to radians, including radian measurement, arc length, areas of sectors and segments, and solving trigonometric equations. It also includes small angle approximations and worked examples on converting angles to radians and degrees, sketching graphs, finding exact values without a calculator, and determining arc lengths of circles. The practical examples and visual aids provided help enhance understanding and application of radian concepts.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
5) Radians 5.1) Radian measure 5.2) Arc length 5.3) Areas of sectors and segments 5.4) Solving trigonometric equations 5.5) Small angle approximations
Chapter CONTENTS 5.1) Radian measure
Your turn Worked example Convert to radians: Convert to radians: 360 2? 180 45 ? 4 90 120 ? 3 60 315 135 7? 4 72 2? 5 720
Your turn Worked example Convert to degrees: Convert to degrees: 5? 900 3? ? 3 ? 2 60 ? 6 5? 6 150 5? 4 9? 4 405 3? 5 4? 5 144
Your turn Worked example Sketch the graph for 0 ? 2? of: Sketch the graph for 0 ? 2? of: ? = cos? ? = sin? ? = tan? Graphs used with permission from DESMOS: https://www.desmos.com/
Your turn Worked example Find the exact values, without a calculator: Find the exact values, without a calculator: 4? 3 7? 6 cos cos 1 2 sin 7? sin 4? 6 3 1 2
Your turn Worked example Sketch the graph for 0 ? 2? of: ? = cos ? +? Sketch the graph for 0 ? 2? of: ? = sin(? +? 4) 2 ? = tan ? ? 3 Graphs used with permission from DESMOS: https://www.desmos.com/
Your turn Worked example Sketch the graph for 0 ? 2? of: ? = sin 2? Sketch the graph for 0 ? 2? of: ? = cos(4?) ? = tan 3? Graphs used with permission from DESMOS: https://www.desmos.com/
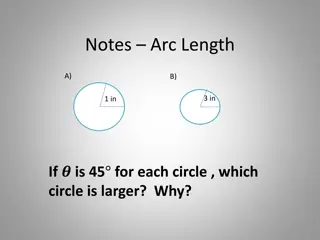
Chapter CONTENTS 5.2) Arc length
Your turn Worked example Find the length of the arc of a circle of radius 5.2 cm, given that the arc subtends an angle of 0.8 radians at the centre of the circle. 4.16 ?? Find the length of the arc of a circle of radius 5.2 cm, given that the arc subtends an angle of 0.4 radians at the centre of the circle. Find the length of the arc of a circle of radius 10.4 cm, given that the arc subtends an angle of 0.2 radians at the centre of the circle.
Your turn Worked example An arc ?? of a circle with radius 7 cm and centre ? has a length of 2.45 cm. Find the angle ??? subtended by the arc at the centre of the circle 0.35 ??? An arc ?? of a circle with radius 0.35 cm and centre ? has a length of 2.45 cm. Find the angle ??? subtended by the arc at the centre of the circle An arc ?? of a circle with radius 0.7 cm and centre ? has a length of 4.9 cm. Find the angle ??? subtended by the arc at the centre of the circle
Your turn Worked example The border of a garden pond consists of a straight edge ?? of length 2.4 m, and a curved part ?, also connecting ? and ?. The curve part is an arc of a circle, centre ?, radius 2 m. Find the length of ?. The border of a garden pond consists of a straight edge ?? of length 4.8 m, and a curved part ?, also connecting ? and ?. The curve part is an arc of a circle, centre ?, radius 4 m. Find the length of ?. 9.99 m
Your turn Worked example A triangle ??? is such that ?? = 8 ??, ?? = 11 ?? and ??? = 0.7 radians. The arc ??, where ? lies on ??, is an arc of a circle with centre ? and radius 8 cm. A region ?, is bounded by the straight lines ?? and ?? and the arc ??. Find the perimeter of ? A triangle ??? is such that ?? = 4 ??, ?? = 5.5 ?? and ??? = 0.35 radians. The arc ??, where ? lies on ??, is an arc of a circle with centre ? and radius 4 cm. A region ?, is bounded by the straight lines ?? and ?? and the arc ??. Find the perimeter of ? 15.7 ?? (3 sf)
Your turn Worked example A sector of a circle of radius 15 cm contains an angle of ? radians. Given that the perimeter of the sector is 42 cm, find the value of ? = 0.8 rad A sector of a circle of radius 30 cm contains an angle of ? radians. Given that the perimeter of the sector is 84 cm, find the value of ?
Your turn Worked example The perimeter of a sector OAB is four times the length of the arc AB. Find the size of angle AOB = 2 rad The perimeter of a sector OAB is four times the length of the arc AB. Find the size of angle AOB
Chapter CONTENTS 5.3) Areas of sectors and segments
Your turn Worked example A circle, centre O, radius 5.2 cm has a minor sector OAB where the arc AB subtends an angle of 0.8 radians at the centre of the circle. Find the area of the sector. 10.816 ??2 A circle, centre O, radius 5.2 cm has a minor sector OAB where the arc AB subtends an angle of 0.4 radians at the centre of the circle. Find the area of the sector. A circle, centre O, radius 5.2 cm has a minor sector OAB where the arc AB subtends an angle of 0.2 radians at the centre of the circle. Find the area of the sector.
Your turn Worked example A circle, centre O, radius 5.2 cm has a minor sector OAB where the arc AB subtends an angle of 0.8 radians at the centre of the circle. A segment is enclosed by a chord AB and the arc AB. Find the area of the segment. 1.12 ??2 (3 sf) A circle, centre O, radius 5.2 cm has a minor sector OAB where the arc AB subtends an angle of 0.4 radians at the centre of the circle. A segment is enclosed by a chord AB and the arc AB. Find the area of the segment. A circle, centre O, radius 5.2 cm has a minor sector OAB where the arc AB subtends an angle of 0.2 radians at the centre of the circle. A segment is enclosed by a chord AB and the arc AB. Find the area of the segment.
Your turn Worked example The area of the minor sector ??? is 28.9 cm2. Given that ??? = 0.8 radians and O is the centre of the circle, calculate the length of the radius 8.5 ?? The area of the minor sector ??? is 14.45 cm2. Given that ??? = 0.4 radians and O is the centre of the circle, calculate the length of the radius
Your turn Worked example A sector of a circle of radius 110 m and perimeter 176 m. Calculate the area of the sector A sector of a circle of radius 110 m and perimeter 352 m. Calculate the area of the sector 1815 ?2
Your turn Worked example OAB is a sector of a circle, centre O, radius 4?. The chord ?? is 5m long. Find the area of the segment. 3.00 ?2 (3 sf) OAB is a sector of a circle, centre O, radius 8?. The chord ?? is 10m long. Find the area of the segment.
Your turn Worked example AB is the diameter of a semicircle, centre O, radius ? cm. C is a point on the semicircle. <BOC = ? radians. Given that the area of AOC is three times the segment enclosed by CB, show that 3? 4sin? = 0 AB is the diameter of a semicircle, centre O, radius ? cm. C is a point on the semicircle. <BOC = ? radians. Given that the area of AOC is six times the segment enclosed by CB, show that 6? 7sin? = 0 Shown
Your turn Worked example OAB is a sector of a circle, centre O, radius 9 cm and angle 0.7 radians. C lies outside the sector. AC is a straight line, perpendicular to OA. OBC is a straight line. Find the area of the region bounded by the arc AB and the lines AC and BC 5.76 ??2 (3 sf) OAB is a sector of a circle, centre O, radius 18 cm and angle 0.35 radians. C lies outside the sector. AC is a straight line, perpendicular to OA. OBC is a straight line. Find the area of the region bounded by the arc AB and the lines AC and BC
Your turn Worked example OPQ is a sector of a circle, centre O, radius 10 cm where <POQ = 0.3 radians. The point R is on OQ such that the ratio OR:RQ is 1:3 A region is bounded by the arc PQ, QR and a line RP. a) Find the perimeter of the region b) Find the area of the region OPQ is a sector of a circle, centre O, radius 20 cm where <POQ = 0.6 radians. The point R is on OQ such that the ratio OR:RQ is 1:3 A region is bounded by the arc PQ, QR and a line RP. a) Find the perimeter of the region b) Find the area of the region a) 18.1 ?? (3 sf) b) 11.3 ??2 (3 sf)
Your turn Worked example Solve in the interval 0 ? 2?: Solve in the interval 0 ? 2?: sin? =1 cos? =1 2 2 ? =? 6,5? 6 tan? = 1
Your turn Worked example Solve in the interval 0 ? 2?: sin? + 1 =1 Solve in the interval 0 ? 2?: cos? + 1 =1 2 2 ? =7? 6,11? 6 tan? 2 = 1
Your turn Worked example Solve in the interval 0 ? 2?: 3sin? + 1 = 0.4 Solve in the interval 0 ? 2?: 5cos? + 2 = 2.3 ? = 3.34,6.08 (3 sf) 4tan? 5 = 1
Your turn Worked example Solve in the interval 0 ? 2?: sin(? ? Solve in the interval 0 ? 2?: cos(? ? 4) =1 2) =1 2 2 ? =5? 12,13? 12 tan(? +? 3) = 1
Your turn Worked example Solve in the interval 0 ? 2?: Solve in the interval 0 ? 2?: 3 3 sin3? = cos5? = 2 2 ? =? 9,2? 9,7? 9,8? 9,13? ,14? 9 9 tan4? = 3
Your turn Worked example Solve in the interval 0 ? 2?: Solve in the interval 0 ? 2?: sin2? =1 cos2? =3 4 4 ? =? 6,5? 6,7? 6,11? 6 tan2? = 3
Your turn Worked example Solve in the interval 0 ? 2?: 2sin2? 5sin? 3 = 0 ? =7? Solve in the interval 0 ? 2?: 2cos2? + 5cos? 3 = 0 6,11? 6 2tan2? 5tan? 3 = 0
Your turn Worked example Solve in the interval 0 ? 2?: 5sin2? 2sin? = 0 ? = 0,0.412,2.73,?,2? Solve in the interval 0 ? 2?: 5cos2? + 2cos? = 0 4tan2? 3tan? = 0
Your turn Worked example Solve in the interval 0 ? 2?: 5cos????? + 2sin? = 0 ? = 0,1.98,?,4.30,2? Solve in the interval 0 ? 2?: 5cos????? + 2cos? = 0
Your turn Worked example Solve in the interval 0 ? < 2?: 2tan? = 3sin? ? = 0,0.841,?,5.44 Solve in the interval 0 ? < 2?: 4tan? = 5cos?
Your turn Worked example Find all the solutions, in the interval 0 ? < 2?, of the equation 2 cos2 ? + 1 = 5 sin?, giving each solution in terms of ?. ? =? Find all the solutions, in the interval 0 ? < 2?, of the equation 2 ???2 ? + 1 = 5 ????, giving each solution in terms of ?. 6,5? 6
Chapter CONTENTS 5.5) Small angle approximations
Your turn Worked example When ? is small, find the approximate value of: sin 2?+tan ? 2? b) ? sin 2? c) sin5? + tan2? cos2? a) 3 2 b) 4 c) 1 When ? is small, find the approximate value of: sin ?+tan 4? 3? b) ? tan 3? c) sin3? + tan4? cos5? a) a) cos 4? 1 cos 6? 1
Your turn Worked example Find the percentage error when calculating the value of cos(0.246 ???) using the small- angle approximations Find the percentage error when calculating the value of cos(0.123 ???) using the small- angle approximations 0.015701% (6 dp)
Your turn Worked example When ? is small, find the approximate value of: 1 2tan? 4cos2? tan2? + 1 When ? is small, find the approximate value of: sin? cos6? 4 sin2? 1 3