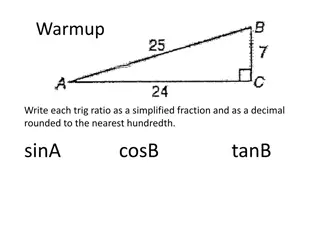
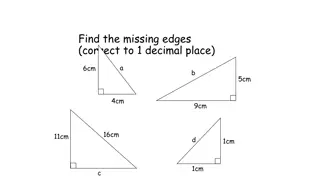
Trigonometry Sine Rule and Ambiguous Case Explained
This content explores the concept of the ambiguous case in trigonometry, specifically focusing on the application of the Sine Rule. Through detailed explanations and illustrations, it clarifies how multiple solutions can arise when certain conditions are met in trigonometric calculations. The author, Culan O'Meara, delves into scenarios where different triangles can be formed with the same given data, leading to a deeper understanding of trigonometric principles and their practical implications.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
LCHL Strand 3: Trigonometry Sine Rule The Ambiguous Case Culan O Meara Ballinrobe Community School
Unit Circle and The Ambiguous Case The word Ambiguous in this context means to be open to or having two possible answers If you observe the Unit Circle here, you can see that Sine is positive in both the 1st(between 0 and 90 ) and 2nd Quadrant (between 90 and 180 ) For Cosine, it is not possible to have more than one answer as Cosine is negative in 2nd Quadrant Author: Culan O'Meara
Sine Rule - The Ambiguous Case The three angles of a triangle add to 180 so it s possible, when given two sides and an angle to draw two triangles that fit the data You can have a triangle with three acute angles and also a triangle that has one obtuse angle and two acute angles Author: Culan O'Meara
Sine Rule - The Ambiguous Case In the example shown, you are given a triangle with sides of length 6 and 8 and an angle of 46 and asked to find the values of the missing angles and sides. You can see that the triangle drawn contains 3 acute angles If you solve this using Sine Rule, you will find that Sin B 0.959 and therefore B 73.6 Author: Culan O'Meara
Sine Rule - The Ambiguous Case However, if we look back at our Unit Circle you will see that there are two angles that will give same answer(same reference angles and Sine is positive in both quadrants) Both 73.6 and 106.4 (180-73.6) have same Sine values Author: Culan O'Meara
Sine Rule - The Ambiguous Case In the triangle shown, we have drawn a different triangle with sides of length 6 and 8 and an angle of 46 You can see that this triangle has B 106.4 Sin 106.4 = Sin 73.6 = 0.959 So having drawn two separate triangles, we finish off the question by finding the remaining angle and side in each case Author: Culan O'Meara
Sine Rule - The Ambiguous Case Author: Culan O'Meara