Trigonometry Review and Essential Concepts Explained
Refresh your knowledge of trigonometry with a thorough review of key concepts such as SOH-CAH-TOA, trigonometric identities, Pythagorean theorem, and more. Understand the significance of standard position, terminal side of angles, unit circle intersections, quadrant signs, and the law of cosines. Explore various trigonometric identities and learn how to apply them effectively in problem-solving. Utilize special triangles to determine angles in a unit circle.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Hopefully, you remember these from last year (you were required to memorize ten of them) plus SOH CAH TOA. If not, you need to know the reciprocal and quotient identities which are in the blue box on pg A17, and the Pythagorean, Addition, and Double-Angle Formulas which are inside the back cover of your books. If you need more information, see the Trig Identity Flash cards information under Chapter 5 of PreCalculus on my website.
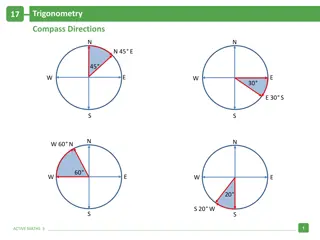
Please review vocabulary on pg A16 regarding standard position, initial side, and terminal side of angles. Remember (see Figure B.9) that the coordinates of the point where your terminal side intersects the unit circle correspond to sine and cosine. P(x,y): the x coordinate is the cosine (adjacent/1 hyp) and the y coordinate is the sine (opposite/1).
Remember that the first quadrant is where x and y are both positive and that the numbering continues counterclockwise. Also, we learned a pneumonic device to remember signs (see Fig. B.13 on pg A18). All Students Take Calculus In quadrant I, All signs are positive for sin, cos, tan and their reciprocals. In quadrant II, only Sin (and its reciprocal) is/are pos. In quadrant III, only Tan (and its reciprocal) is/are pos. In quadrant IV, only Cos (and its reciprocal) is/are pos.
The law of cosines helps to find an unknown angle when you are given SSS (side, side, side) or the unknown side when you are given SAS and the triangle is not a right triangle. Law of Cosines: c = a + b - 2abcos There is a proof on page A20 if you are interested.
There are many other Trigonometric Identities and Formulas in this Appendix and inside the back cover of your book. You should be familiar with them and know how to use them, but you do not need to memorize them.
Use the information from slides #3 and #4 to draw the appropriate triangle(s) in a unit circle. Work backwards using special triangles to determine the appropriate angle. See example 6 on pages A22&A23.
If is the smallest angle measured counterclockwise from the x-axis, then the slope of the line is the same as the tan . m= tan This makes sense because m = rise/run and tan = (sin )/(cos ), the rise is the opposite side (y=sin ) and the run is the adjacent side (x=cos ). See figures B.19 & B.20 on pg. A23.