Review: Design Eq & Conversion
Design equations for batch, flow, CSTR, PFR, and PBR systems are discussed, emphasizing the calculation of conversion and reactor volumes. The importance of understanding reaction rates and stoichiometry in determining reactor sizes is highlighted, along with numerical evaluation techniques for inte
0 views • 25 slides
Understanding Integral Calculus: Two Major Approaches & Antiderivatives
In this chapter, we delve into the fundamental concepts of integral calculus, focusing on two major approaches to mathematically generate integrals and assigning physical meanings to them. We explore antiderivatives, differentiation, integration, and the process of taking integration as the inverse
2 views • 59 slides
Tight Binding Model Adapted for Graphene from Kittel Chapter 9
This content discusses the tight binding model adapted for graphene based on Kittel Chapter 9, covering topics such as Bloch conditions, hybridization, sublattices, and overlap integrals. It explores the uniqueness of graphene's structure and its impact on coefficients in the calculations.
0 views • 16 slides
Understanding Numerical Methods for Approximating Analytic Equations
Introduction to approximating solutions to analytic equations, focusing on differential equations, integral equations, and integro-differential equations. Exploring ordinary and partial derivatives, differential and integral equations, and the involvement of unknown functions and their derivatives a
2 views • 15 slides
Trigonometric Integrals: Strategies and Identities
Learn useful trigonometric identities and strategies for integrating powers of sine and cosine. Understand when to use Pythagorean, Half or Double Angle Identities, and how to handle odd or even powers efficiently. Examples provided for clarity.
1 views • 14 slides
Calculus I Lecture #13: Volumes of Solids and Solids of Revolution
Exploring the concepts of finding volumes of solids using integrals, by slicing solid objects with parallel planes and calculating cross-sectional areas. Examples include calculating the volume of a pyramid and a curved wedge. The method of solids of revolution using the disk method is also discusse
0 views • 12 slides
Review of Definite Integrals using the Residue Theorem
Singular integrals involving logarithmic and non-integrable singularities are discussed, emphasizing integrability in the principal value sense. Cauchy Principal Value integrals and examples of their evaluations for singularities like 1/x are explored, highlighting the necessity of passing through t
0 views • 48 slides
Overview of Semi-Empirical Methods Based on Hartree-Fock
Semi-empirical methods derived from Hartree-Fock theory aim to reduce computational effort by approximating or eliminating electron repulsion integrals. Strategies include introducing adjustable parameters to replace ERI calculations and utilizing zero differential overlap methods like CNDO, INDO, N
1 views • 11 slides
Understanding Accumulation Problems and Definite Integrals in Applied Calculus
Explore the interpretation of definite integrals in accumulation problems, where rates of change are accumulated over time. Learn how to solve accumulation problems using definite integrals and avoid common mistakes by understanding when to use initial conditions. Discover the relation between deriv
0 views • 9 slides
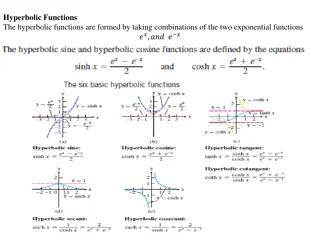
Understanding Hyperbolic Functions and Their Inverses
This content delves into the world of hyperbolic functions, discussing their formation from exponential functions, identities, derivatives, and inverse hyperbolic functions. The text explores crucial concepts such as hyperbolic trigonometric identities, derivatives of hyperbolic functions, and integ
0 views • 9 slides
Understanding Fourier Analysis and Its Applications
Fourier analysis is essential in representing periodic functions using Fourier series, allowing for solving differential equations and approximating complex functions. The method extends to nonperiodic phenomena through Fourier integrals and transforms, with significant applications in engineering a
0 views • 21 slides
Understanding Loop Structures in Python Programming
This lecture covers Loop Structures, specifically focusing on the while statement and nested loops in Python programming. It discusses the Fibonacci sequence and demonstrates how to write a program to compute the nth Fibonacci number. Additionally, it explains the difference between definite and ind
3 views • 22 slides
Understanding Completing Sentences in English Grammar for Classes 9-10
Delve into the concept of completing sentences with Assistant Teacher Z.M. Akhtarul Kabir from Wazuddin High School. Learn the definition, rules, and examples of completing sentences with various tenses like present indefinite, past indefinite, and past perfect. Enhance your grammar skills and abili
0 views • 17 slides
Understanding the Residue Theorem in Complex Analysis
The Residue Theorem is a powerful tool in complex analysis that allows us to evaluate line integrals around paths enclosing isolated singularities. By expanding the function in a Laurent series, deforming the contour, and summing residues, we can evaluate these integrals efficiently. This theorem ex
0 views • 31 slides
Understanding Integration: Geometrical Interpretation, Properties, and Methods
Integration is the inverse process of differentiation, where we find a function whose differential is given. This process involves basic formulae, methods like integration by parts, and geometrical interpretation. Properties of indefinite integrals and techniques such as integration by substitutions
6 views • 28 slides
Understanding Numerical Integration in Density Functional Theory (DFT)
The application of numerical integration techniques in Density Functional Theory (DFT) is crucial for solving the Eigenvalue Problem and evaluating energy functionals. This involves partitioning integrals, approximating integrals at atomic centers, defining partition functions, and ensuring cell fun
0 views • 15 slides
Understanding Indefinite Pronouns: A Tale of Everybody, Somebody, Anybody, and Nobody
This story highlights the importance of recognizing indefinite pronouns such as everybody, somebody, anybody, and nobody. Through the tale of four individuals and a task left undone, the narrative emphasizes the roles of common, singular, and plural indefinite pronouns in subject-verb agreement. Exp
0 views • 11 slides
Understanding Indefinite Pronouns in English
In English grammar, indefinite pronouns are used to refer to unnamed people, things, or places. They can be affirmative, negative, or used in questions. Examples like "some," "any," and their variations are common in everyday conversations. Learn how to use them correctly to convey the intended mean
0 views • 8 slides
Practice Indefinite Pronouns with ESL Puzzles
Enhance your understanding of indefinite pronouns like someone, nobody, anybody, and everybody with these engaging ESL puzzles. Test your knowledge in various scenarios and improve your English skills effortlessly. Discover new ways to use indefinite pronouns in sentences and boost your confidence i
0 views • 12 slides
Gender and the Indefinite Article in French
In French, nouns have genders (masculine or feminine) and are accompanied by definite articles (un or une) based on their gender. Learning the gender of nouns is essential as it cannot be guessed from the meaning or appearance. The indefinite article "a" is represented by un for masculine nouns and
0 views • 12 slides
Understanding Python Loops: While, Nested Loops, and List of Tuples
Python loops come in two types - definite loops (like for loops) and indefinite loops (like while loops). While loops are used for conditional iteration, repeating as long as a condition is true. On the other hand, for loops are ideal for situations where the number of iterations is known in advance
0 views • 25 slides
Exploring Geometric Probabilities: From Fractions to Integrals
Delve into the realm of geometric probabilities with insights on how to transition from fractions to definite integrals, utilizing technology for enhanced learning experiences. Understand the significance of probability calculations in quantifying likelihood, incorporating geometric representations
0 views • 26 slides
Understanding Singular and Plural Indefinite Pronouns
Explore the difference between singular and plural indefinite pronouns with examples. Learn about singular indefinite pronouns like 'each' and 'nobody', plural ones such as 'several' and 'few', and those that can be both singular and plural like 'some' and 'all'.
0 views • 5 slides
Understanding Coulomb Interaction in Many-Particle Hamiltonian
Explore the treatment of Coulomb interaction in a many-particle Hamiltonian, where careful integration is crucial due to divergence issues. Learn about solving the Coulomb Hamiltonian with Slater integrals and expanding the operator on spherical harmonics for analytical solutions. Discover the signi
0 views • 15 slides
Understanding Coulomb Repulsion and Slater Integrals
Dive into the intricate world of Coulomb repulsion and Slater integrals, essential concepts in quantum physics. Explore the challenges posed by the diverging Coulomb integral and the complex calculations required to evaluate these interactions. Discover how Slater integrals play a crucial role in cr
0 views • 14 slides
Mastering Definite and Indefinite Articles in English Grammar
Delve into the intricacies of definite and indefinite articles in English grammar through understanding their usage with examples and pretests. Learn how native speakers employ articles to convey particularity or generality before nouns, differentiate between specific and nonspecific items, and gras
0 views • 14 slides
Applications of Definite Integrals in Finding Areas
Explore the practical applications of definite integrals through the concept of finding areas. These images illustrate how definite integrals are used to calculate areas bounded by curves and lines, offering a visual representation of the integral calculus in action.
0 views • 9 slides
Understanding Area, Riemann Sums, and Definite Integrals
Antiderivatives are utilized to find area under curves, where Riemann Sums are employed for approximations. The process involves dividing intervals into rectangles for both approximate and exact area calculations. Definite integrals provide specific, finite values representing total displacement, wi
0 views • 8 slides
Exploring Properties of Definite Integrals in Mathematics II Second Semester
Delve into the world of definite integrals in Mathematics II Second Semester, understanding rules, properties, and applications through examples. Learn to find bounds, evaluate integrals, calculate areas under curves, and graph functions for a comprehensive understanding of this mathematical concept
0 views • 15 slides
Understanding the Fundamental Theorem of Calculus
Explore the connection between differential calculus and the definite integral through the fundamental theorem of calculus, which allows for the evaluation of complex summations. Discover the properties of definite integrals and how to apply the theorem to find areas under curves. Practice evaluatin
0 views • 15 slides
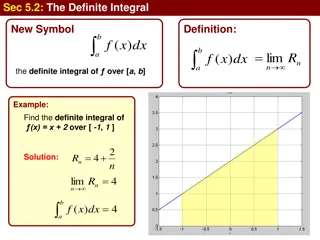
Understanding Definite Integrals in Calculus
Explore the concept of definite integrals in calculus, including their new symbol definition, area interpretation, and examples of evaluating integrals in terms of areas. Learn about the limits of integration, the procedure of integration, and how definite integrals can represent areas under curves.
0 views • 34 slides
Definite Integrals Using Graphing Display Calculator for Evaluation
Learn how to use a Graphing Display Calculator (GDC) to evaluate definite integrals step-by-step. Follow the instructions provided in the images to input the function and calculate the result with the GDC. This interactive process helps in understanding how technology can assist in mathematical comp
0 views • 17 slides
Understanding Definite Integrals in Mathematics
Explore the concept of definite integrals in mathematics, covering properties, solving methods, and applications in finding areas bounded by curves. Prior knowledge of functions, limits, derivatives, and indefinite integrals is essential to grasp this topic effectively. Dive into the unique value of
0 views • 32 slides
Understanding the Use of Articles: Indefinite and Definite Determiners
Explore the uses of indefinite determiners (articles "a" and "an") in different contexts such as introducing nouns, expressing quantities, class examples, and more. Learn important rules regarding their usage, including when to use "a" and "an" before nouns and adjectives. Additionally, discover the
0 views • 13 slides
Understanding Integration and Antiderivatives
Exploring the concepts of definite and indefinite integrals, Riemann sums, and antiderivatives in calculus. Learn about interpreting the definite integral, Riemann sums as rectangles approximating integrals, and finding general antiderivatives. Discover various formulas for finding antiderivatives o
0 views • 16 slides
Analytical Integration of Functions: A Comprehensive Guide
Functions and their integrals are explored in this guide, covering definitions, simple integration cases, examples, and well-known integrals. Learn about differential equations, inspection integration, and trigonometric functions. Master the techniques with detailed explanations and examples.
0 views • 20 slides
Understanding Indefinite Pronouns in English
Indefinite pronouns in English express the ideas of all, any, none, or some. Examples include all, everybody, anyone, nobody, something, somewhere, and more. Learn how to use indefinite pronouns correctly in sentences to convey different meanings and concepts.
0 views • 16 slides
Methods of Integration and Trigonometric Substitution
Explore methods of integration including integration by parts and trigonometric substitution. Learn how to apply these techniques to solve integrals involving logarithmic, trigonometric, and rational functions. Discover step-by-step processes and identities to simplify and evaluate various types of
0 views • 7 slides
An Lp Theory for Outer Measures and Applications to Singular Integrals II
This content delves into the theory of outer measures, focusing on its application to singular integrals. It covers topics such as Carleson boxes, outer measures on the upper half-plane, sizes of functions on tents, outer essential supremum spaces, Lp spaces, embedding theorems, and weak L1-Sinfty e
0 views • 34 slides
Asymptotic Evaluation Techniques in Integral Calculus
Learn about asymptotic evaluation of integrals through techniques like integration by parts and the stationary-phase method. Understand how to handle integrals involving real functions, and grasp the significance of concepts like the Riemann-Lebesgue lemma and small o notation. Delve into the physic
0 views • 21 slides