Understanding Definite Integrals in Calculus
Explore the concept of definite integrals in calculus, including their new symbol definition, area interpretation, and examples of evaluating integrals in terms of areas. Learn about the limits of integration, the procedure of integration, and how definite integrals can represent areas under curves. Dive into interpreting integrals in terms of areas and understanding the net area concept. Discover how to evaluate different integrals using the area interpretation method.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
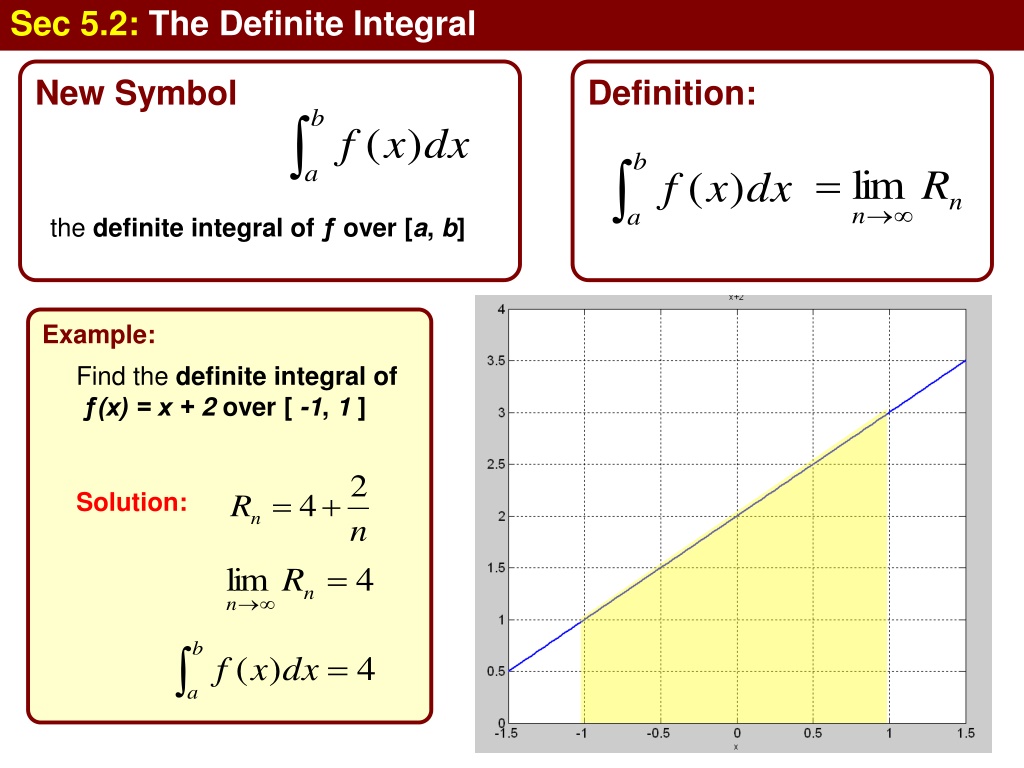
Sec 5.2: The Definite Integral New Symbol Definition: b ( ) f x dx b = lim a R ( ) f x dx n n a the definite integral of over [a, b] Example: Find the definite integral of (x) = x + 2 over [ -1, 1 ] 2 = 4+ Solution: Rn n = lim n 4 R n b = ( ) 4 f x dx a
Sec 5.2: The Definite Integral Note 1: integrand limits of integration b ( ) f x dx upper limit b lower limit a a Integral sign The dx simply indicates that the independent variable is x. The procedure of calculating an integral is called integration.
Sec 5.2: The Definite Integral Area under Limit of the Riemann sum the curve lim R n n If you are asked to find one of them choose the easiest one. the definite integral of f from a to b b ( ) f x dx a three sides of the same coin
Sec 5.2: The Definite Integral Example: Evaluate the following integrals by interpreting each in terms of areas. 6 2dx x 0
Sec 5.2: The Definite Integral 1 A a 2 A b a a b b b b a a = b = + ( ) f x dx ( ) f x dx = ( ) f x dx A A 1 2 a definite integral has negative value the definite integral can be interpreted as the area under the curve A definite integral can be interpreted as a net area, that is,a difference of areas:
Sec 5.2: The Definite Integral Example: Evaluate the following integrals by interpreting each in terms of areas. 8 = x + ( ) 2 f x 4 6 4 + ( ) 2 x dx 2 2 4 6 4 2
Sec 5.2: The Definite Integral Example: Evaluate the following integrals by interpreting each in terms of areas. 3 ) ( ) 1 b x dx 0 Example: Evaluate the following integrals by interpreting each in terms of areas. 0 1 2 ) 1 a x dx
Sec 5.2: The Definite Integral Term-121
Sec 5.2: The Definite Integral lim R Express the limit as a definite integral on the given interval. n n = lim L n n = lim M n n ? ??? ? + ???? ? the definite integral of f from a to b b ( ) f x dx a
Sec 5.2: The Definite Integral Term-103 ? =2 ??=2? ? ? ? ??= ? ?? x ?=1 ? (2 ?+3? ??= ?2) ?=1 ? (1 +3? 2?)2 = ? ?=1 ? ? (1 + (3 4)2? ?)2 (1 +3 4??)2 = = ? ? ?=1 ?=1
Sec 5.2: The Definite Integral Area under lim R n the curve = lim n L n n = lim M n n the definite integral of f from a to b If you are asked to find one of them choose the easiest one. b ( ) f x dx a
Sec 5.2: The Definite Integral Term-121
Sec 5.2: The Definite Integral 4 L M R 4 4 In fact, instead of using left endpoints or right endpoints, we could take the height of the ith rectangle to be the value of f at any number in the ith subinterval * [ , ] ix x x 1 i i S * * * 3 * 4 We call the numbers the sample points 2 1 , x x , , 4 x x n = i = *) ( S f x x n i 1 Definition: Definition: lim R lim S Area = Area = n n n n * * * 3 x * 2 x 4 x 1x
Sec 5.2: The Definite Integral Definition: Definition: a b = lim ( ) f x dx S b n = lim R ( ) f x dx n n n a Example: S Find the Riemann sum for (x) = x + 2 over [ 0, 5 ] 4 3 , 0 [ 4 , 3 [ ], ] 5 , 4 [ ], divided into = , 2 . 3 = = * , 1 * * 9 . 4 x x x 1 2 3 ?3= 3 3 + 1 5.2 + (1)(6.9) * * * 3 x * 2 x 4 x 1x
Sec 5.2: The Definite Integral Area under lim = lim R L n n the curve n n = lim M n n S = maxlim n 0 x i the definite integral of f from a to b If you are asked to find one of them choose the easiest one. b ( ) f x dx a
Sec 5.2: The Definite Integral Properties of the Integral Property (1) a b = ( ) ( ) f x dx f x dx b a Example: ( ) ( ) 0 = 2 2 cos cos x x dx x x dx 0
Sec 5.2: The Definite Integral Property (2) a = ( ) 0 f x dx a
Sec 5.2: The Definite Integral Property (3) b c b = + ( ) ( ) ( ) f x dx f x dx f x dx a a c
Sec 5.2: The Definite Integral Property (4) b b = ( ) ( ) c f x dx c f x dx a a Property (5) a b b b + = + ( ) ( ) ( ) ( ) f x g x dx f x dx g x dx a a b b b = ( ) ( ) ( ) ( ) f x g x dx f x dx g x dx a a a
Sec 5.2: The Definite Integral Properties of the Integral
Sec 5.2: The Definite Integral ? integrable Definition: Example: Find the definite integral of (x) = x + 2 over [ -1, 1 ] b = lim R ( ) f x dx n a n provided that this limit exists 2 = 4+ Solution: Rn n = lim n 4 R Definition: n If the limit does exist, we say that the function f is integrable the limit exist, = x + ( ) 2 f x is integrable
Sec 5.2: The Definite Integral Theorem: If f (x) is continuous on [a, b] f (x) is integrable Example: = ] 1 , 0 ( 0 0 x = ( ) f x x 1 x is not integrable in [0, 1] Remark integrable ) (x f f(x) has only finite number of removable discontinuities b ( ) exist dx f x a Remark integrable ) (x f f(x) has only finite number of jump discontinuities b ( ) exist dx f x a
Sec 5.2: The Definite Integral Term-091
Sec 5.2: The Definite Integral Property b = b ( c - a) c dx a c 4 = 5 dx a b 2
Sec 5.2: The Definite Integral min ( ) max f f x f max f min f a b b Property (6) ( )( ) ( )( ) a min ( ) max f b a f x dx f b a
Sec 5.2: The Definite Integral Property (7) (x ) f ( ) ( ) f x g x (x ) g b b a a ( ) ( ) f x dx g x dx a b
Sec 5.2: The Definite Integral Term-082