Review: Design Eq & Conversion

Design equations for batch, flow, CSTR, PFR, and PBR systems are discussed, emphasizing the calculation of conversion and reactor volumes. The importance of understanding reaction rates and stoichiometry in determining reactor sizes is highlighted, along with numerical evaluation techniques for integrals. Examples and illustrations provided by Prof. M.L. Kraft from the University of Illinois.

• Reactor design
• Conversion calculations
• Chemical engineering
• Reaction rates
• Numerical integration

allyson Follow

Uploaded on Mar 13, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

Presentation Transcript

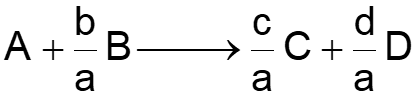
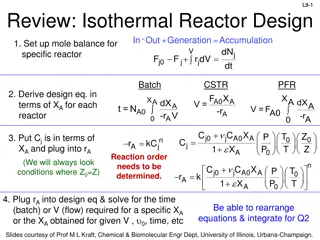
1. L4-1 Review: Design Eq & Conversion d C a a moles j stoichiometric coefficient; positive for products, negative for reactants b c moles reacted A + + A B D XA A fed a BATCH SYSTEM: = + X N N N X = = + N N N N X j j 0 j j A 0 A T j T 0 j A 0 A j A dX dX Ideal Batch Reactor Design Eq with XA: A V A = = t N N r V 0 A 0 A 0 A r dt A FLOW SYSTEM: = + F F F X = = + F F F F X j j 0 j j A 0 A T j T 0 j A 0 A j Ideal CSTR Design Eq with XA: F V X A dX dX Ideal SS PFR Design Eq with XA: A A = = V F F r 0 A 0 A 0 A r dV A X A dX X dX Ideal SS PBR Design Eq with XA: A A 0 A A = W F = = F r ' 0 A 0 A 0 A r ' dW r A A Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.

2. L4-2 Review: Sizing CSTRs We can determine the volume of the CSTR required to achieve a specific conversion if we know how the reaction rate rj depends on the conversion Xj Ideal SS CSTR design eq. Volume is product of FA0/-rA and XA F X F A 0 A A r 0 = = CSTR V CSTR V X A r A A Plot FA0/-rA vs XA (Levenspiel plot) VCSTR is the rectangle with a base of XA,exit and a height of FA0/-rA at XA,exit Area = Volume of CSTR FA0 rA FA0 rA V = X1 X1 X1 X Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.

3. L4-3 Review: Sizing PFRs & PBRs We can determine the volume (catalyst weight) of a PFR (PBR) required to achieve a specific Xj if we know how the reaction rate rj depends on Xj exit , A X 0 A PFR F V = design eq. X Ideal PFR exit , A F dX A r 0 A dX = PFR V A r A A 0 , 0 A X X A exit exit , F dX Ideal PBR design eq. A r 0 A dX = = W F W PBR A 0 PBR A r A A 0 0 Plot FA0/-rA vs XA (Experimentally determined numerical values) VPFR (WPBR) is the area under the curve FA0/-rA vs XA,exit Area = Volume of PFR Area = VPFR or Wcatalyst, PBR FA0 rA X FA0 rA F 1 X X1 A F 1 A 0 V = 0 = dX W V dX A 0 dX = 0 r r ' A 0 X1 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.

4. L4-4 Numerical Evaluation of Integrals (A.4) Simpson s one-third rule (3-point): 2 X f ( ) ( ) ( ) 1 0 0 2 0 1 X X h = Trapezoidal rule (2-point): 1 X h dx x f = h ( ) x ( ) ( ) ( ) + = + + f X f X dx f X f 4 X f X 0 1 2 3 0 X X 2 0 = = + h X X h 1 0 2 Simpson s three-eights rule (4-point): = + = + X X h X X 2 h 1 0 2 0 X 3 3 3 ( ) x ( ) ( ) ( ) ( ) X X = f 3 + f 3 + + f dx h f X X X f X 0 = h 0 1 2 3 8 3 0 Simpson s five-point quadrature : 0 X f 3 X 4 X X 4 h ( ) x ( ) ( ) ( ) ( ) ( ) 0 = h = + + + + f dx f 4 X f 2 X f 4 X f X 1 2 3 4 4 0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.

5. L4-5 Review: Reactors in Series F A0 If is monotonically increasing then: r - A 2 CSTRs 2 PFRs + PFR V PFR V CSTR V i j + CSTR V VCSTR2 PFR V CSTR V VPFR2 VCSTR1 i j VPFR1 PFR CSTR CSTR PFR VCSTR1 + VPFR2 VPFR1 + CCSTR2 VCSTR2 VCSTR1 VPFR2 VPFR1 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.

6. L4-6 L4: Rate Laws & Stoichiometry X X X F X dX r dX dX A A A A0 r A A V A A V = t N V F W F = = = A0 A0 A0 Ar r ' A 0 0 0 A A Reaction Rates ( rA ) 1. Concentration 2. Temperature 3. Reversible reactions How to derive an equation for rA [ rA = f(XA)] 1. Relate all rj to Cj 2. Relate all Cj to V or u 3. Relate V or u to XA 4. Put together Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.

7. L4-7 Concentration and Temperature Molecular collision frequency concentration Rate of reaction concentration At constant temperature : r = f(CA, CB, .) CA : Concentration of A CB : Concentration of B As temperature increases, collision frequency increases Rate of reaction = f [( CA, CB, ), (T)] ( ) ( T ) = -r k f C ,C ,... A A A B Specific rate of reaction, or rate constant, for species A is a function of temperature Reaction rate is a function of temperature and concentration Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.

8. L4-8 Elementary Reactions & Rate Laws Dependence of reaction rate rA on concentration of chemical species in the reaction is experimentally determined Elementary reaction: involves 1 step (only) Stoichiometric coefficients in an elementary reaction are identical to the powers in the rate law: = + r k C C A B C A A A B Reaction order: order with respect to A order with respect to B Overall reaction order n = + Zero order: -rA = kA 1st order: -rA = kACA 2nd order: -rA = kACA2 3rd order: -rA = kACA3 k is in units mol/(volume time) k is in units time-1 k is in units volume/(mol time) k is in units volume2/(mol2 time) Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.

9. L4-9 Overall Stoichiometric Equations Overall equations describe the overall reaction stoichiometry Reaction order cannot be deduced from overall equations Examples: 2 NO r = k NO NO C C + 2NO O 2NO O2 2 2 This reaction is not elementary, but under some conditions it follows an elementary rate law Forward reaction is 2nd order with respect to NO and 1st order with respect to O2 (3nd order overall) Compare the above reaction with the nonelementary reaction between CO and Cl2 3 2 CO r = kC C + CO Cl COCl CO Cl2 2 2 Forward reaction is 1st order with respect to CO and 3/2 order with respect to Cl2 (5/2 order overall) Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.

10. L4-10 Specific Rate Constant, kA kAis strongly dependent on temperature Ae ( ) T E RT = k Arrhenius Equation A Where : A = Pre-exponential factor or frequency factor (1/time) E = Activation energy, J/mol or cal/mol R = Gas constant, 8.314 J/mol K (or 1.987 cal/mol K) T = Absolute temperature, K E 1 R T Taking ln of both sides: = lnk lnA -E/R ln k To determine activation energy E, run the reaction at several temperatures, and plot ln k vs 1/T. Slope is E/R 1/T Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.

11. L4-11 Reversible Reactions kA kA + + aA b B c C d D a b a b = = fA r k C C fA r k C C Rate of disappearance of A (forward rxn): A A B A A B c d = bA r k C k C C Rate of generation of A (reverse reaction): C A C D a b c d = = + = + A,net r r fA r bA r r k C C A A A A B A C D At equilibrium, the reaction rate is zero, rA=0 a b c A A B A C k C C k C = + d a b c d = = r 0 C k C C k C C A D A A B A C D c d Thermodynamic equilibrium relationship C C C C k k C D A = = K C a b KC: concentration equilibrium constant (capital K) A A B H 1 T 1 T KC is temperature dependent (no change in moles or CP): RX R = K (T) K (T )exp C C 1 1 HRX: heat of reaction If KC is known for temperature T1, KC for temperature T can be calculated Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.

12. L4-12 L4: Rate Laws & Stoichiometry X X X F X dX r dX dX A A A A0 r A A V A A V = t N V F W F = = = A0 A0 A0 Ar r ' A 0 0 0 A A Reaction Rates ( rA ) 1. Concentration 2. Temperature 3. Reversible reactions How to derive an equation for rA [ rA = f(XA)] 1. Relate all rj to Cj 2. Relate all Cj to V or u 3. Relate V or u to XA (Wednesday) 4. Put together (Wednesday) Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.

13. L4-13 1. Relate all rjto Cj rA as a function of Cj is given by the rate law The rate relative to other species (rj) is determined by stoichiometry b c d + + A B a C D A is the limiting reagent a a r r r rj is negative for reactants, positive for products C B D = = = r ( ) ( ) ( ) A b a c a d a r j stoichiometric coefficient positive for products, negative for reactants j r = In general: A j b c d = = 1 = = a a B A c d a Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.

14. L4-14 For the reaction disappearance is 2 mol/dm3 s (-rO2= 2 mol/dm3 s). the rate of O2 + 2NO O 2NO 2 2 What is the rate of formation of NO2? r j Hint: r = A j rNO2 = 4 mol/dm3 s r ( ) NO 2 1 2 2 r r r = = O NO ( ) O 2 2 2 mol dm mol dm 2 2 r 4 r = = NO NO 3 3 2 2 s s Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.

15. L4-15 2a. Relate all Cjto V (Batch System) Reaction rate is a function of Cj: = r k C N V C mol L A A A B j = = Batch: C How is Cj related to V and XA? j b c d = + + + N N N X A B a C D j 0 j j A 0 A a a ( ) N Put NA in terms of XA: N N X A A0 A0 V A = C = C A A V b a ( ) N N X Do the same for species B, C, and D: B0 A0 A N V B = = C B V c a d a + + ( ) ( ) N N X N N X C0 A0 A D0 A0 A N V N V C D = = = = C C C D V V Cj is in terms of XA and V. But what if V varies with XA? That s step 3a! Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.

16. 2a. Additional Variables Used in Textbook b A + L4-16 c d + B a C D a a bN a V ( ) N X B0 A0 A N V B = = C B N N C C Book uses term i: i 0 0 i = i = A0 A 0 So species Ni0 can be removed from the equation for Ci N N N N b a V ( ) A0 1 B0 A 0 X A N A0 A 0 = C Multiply numerator by NA0/NA0: B bX a N A 0 B A b a = = C C C X B B A0 B A V Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.

17. L4-17 3a. Relate V to XA(Batch System) Volume is constant (V = V0) for: Most liquid phase reactions Gas phase reactions if moles reactants = moles products ( ) ( ) 2 CO g H O g + If the volume varies with time, assume the equation of state for the gas phase: At time t: PV = ZNTRT and at t=0: P0V0 = Z0NT0RT0 P: total pressure, atm NT: total moles R: ideal gas constant, 0.08206 dm3 atm/mol K Want V in terms of XA. First find and expression for V at time t: P V V P d c N N N a a ( ) g ( ) g + CO H 2 2 Z: compressibility factor T: temperature, K What is NT at t? N N ZN RT T T Z Z PV 0 T T = = 0 0 0 P V 0 T0 Z N RT 0 0 T0 0 b a = = + + = + NT at time t is: 1 N X N N N X T j T0 A0 A T T0 A0 A j d a c a b a change in total # moles Moles A reacted + = where = 1 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.

18. L4-18 3a. Relate V to XA(continued) d c where = a a b a change in total # moles Moles A reacted = + + = N N N X 1 T T0 A0 A P P N N T T Z Z Can we use the eq. for NT above to find an expression for NT/NT0? 0 T = V V 0 0 0 T0 N N N N N N N N T0 A0 T A0 = + S ubstitut e: y = =mole fraction of A ini t ially pr esent X A0 A T0 T0 T0 T0 N N N N T T = + 1 = + 1 y X X = = S ubsti tute : y e xpans ion facto r A0 A A A0 T0 T0 P P N N N N T T Z Z 0 T T = + = Plug : 1 X into V V A 0 T 0 0 0 T0 P P T T Z Z ( ) 0 = + V V 1 X 0 A 0 0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.

19. L4-19 What is the meaning of ? P P T T Z Z ( ) 0 = + V V 1 X where 0 A 0 0 N N d a c a b a A0 = = + expansion factor: y 1 A0 T0 N N If we put the following equation in terms of : T = + 1 X A T0 N N N N X N N T T0 T T0 T = 1 = = X X A A N N T0 T0 T0 A = N N Change in total # moles at X total moles fed 1 When conversion is complete (XA=1): Tf T0 A = = N T0 The expansion factor, , is the fraction of change in V per mol A reacted that is caused by a change in the total number of moles in the system Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.

20. L4-20 4a. Put it all together (batch reactor) N N N X + = + N V N N V X j j0 j A 0 A j j j A A 0 0 Batch: = = C C j j + N N N X P P T T Z Z j j0 j A0 Z Z A ( ) 0 = = C = + V V 1 X j 0 A V P P T T ( ) 0 0 0 + V 1 X 0 A 0 0 N + 1 C C X T T Z Z P P 0 i = C 0 j A0 X j A 0 0 = C i0 V j + 0 A 0 For a given XA, we can calculate Cj and plug the Cj into rA=kCjn What about flow systems? Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.

21. L4-21 2b. Relate all Cjto u (Flow System) Reaction rate is a D a a a b c d + + A B C = r k C C A A A B function of Cj: How is Cj related to u and Xj? F u mol s L s mol L j = + F F F X = = = C Flow: j 0 j j A 0 A j ( ) F u Put FA in terms of XA: F A0 F u X A A0 A = C = C A A b a ( ) B0 F F X Do the same for species B, C, and D: A0 A F u B = = C B u c a d a + + ( ) ( ) C0 F F X D0 F F X A0 A A0 A F u F u C D = = = = C C C D u u We have Cj in terms of XA and u, but what if u varies with XA? That s step 3b! Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.

22. L4-22 3b. Relate u to XA(Flow System) Start with the equation of state for the gas phase: = PV ZN RT T N V P Rearrange to put in terms of CT, where CT = NT/V: T = = C T ZRT Rearrange to put in terms of u: 1 P Can we relate CT to u? F u F u P T = u T F ZRT = = C T T ZRT F P What is CT0 at the entrance of the reactor? T0 u 0 = = C T0 Z RT 0 0 0 Use these 2 equations to put u in terms of known or measurable quantities 1 = u T0 0 F Z RT Put in terms of u0: 0 0 P 0 ( ) F ZRT 1P u u P P F F Z Z T T T Z RT 1P 0 T = u = u ( ) 0 T0 0 F 0 0 0 T0 0 0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.

23. L4-23 3b. Relate u to XA(continued) = T0 0 0 F Z T P P F Z T = + subst itute in : F F F X and simplify 0 T u u T T0 A0 A 0 ) ) u + F F X P P F X P P Z Z T T Z Z T T T0 A0 A 0 A F 0 A 0 u = u u = u + 1 0 0 F T0 0 0 T 0 0 0 ( ( u N N V V F N N F A0 0 A0 F A0 A0 F = = = = Simplify wit h : y Because y A0 A0 T0 T0 T0 0 T0 ) P P Z Z T T ( 0 : = u = u + substitute y 1 y X A0 0 A0 A 0 0 ) P P Z Z T T ( 0 u = u + 1 X 0 A 0 0 N N Change in total # moles at X =1 total moles fed When conversion is complete (XA=1): Tf T0 A = = N T0 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.

24. L4-24 4b. Put it all together (flow reactor) F F F + = 0 X + F u F F V X j j j A A 0 j j0 j A 0 A Flow: = = C C j j + F u F F X P P T T Z Z j j0 j A Z Z 0 A ( ) 0 = = C u = u + 1 X j 0 A P P T T ( ) 0 0 0 u + 1 X 0 A 0 0 iF u + 1 C C X T T Z Z P P 0 = C 0 j A0 X j A 0 0 = C i0 j + 0 A 0 This is the same equation as that for the batch reactor! For a given XA, we can calculate Cj and plug the Cj into rA=kCjn Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.

25. L4-25 4. Summary: Cjin terms of Xj + = = 0 P T N V N j A0 N Z Z X j j0 A N V C Batch: j0 j = C P T j0 ( ) 0 + V 1 X 0 0 A 0 + + C C X T T Z Z P P j0 A0 X j A 0 0 = C j 1 A 0 + F u F j A0 F P P X j j0 A T T F u = = C Flow: j0 j = C Z Z j0 ( ) 0 u + 1 X 0 A 0 0 0 + + C C X T T Z Z P P j0 A0 X j A 0 0 = C j 1 A 0 This is the same equation as that for the batch reactor! For a given XA, we can calculate Cj and plug the Cj into rA=kCjn Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.