Understanding Area, Riemann Sums, and Definite Integrals
Antiderivatives are utilized to find area under curves, where Riemann Sums are employed for approximations. The process involves dividing intervals into rectangles for both approximate and exact area calculations. Definite integrals provide specific, finite values representing total displacement, with properties and rules like the Trapezoid Rule offering further insights. Various homework exercises are suggested for practice.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
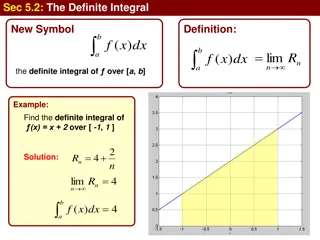
4.2/4.3 Area, Riemann Sums & Definite Integrals
*Antiderivatives can be used to find area under a curve. Some antiderivatives can t be found directly so we must approximate them using Riemann Sums.
Riemann Sums We find the area under a curve, both approximate and exact, by dividing the interval into rectangles. *more rect. more accurate approx. *as # rectangles , we approach the exact area
On : Width of a rectangle: n= # of rectangles *can use left endpoints, right endpoints, or midpoints
Definite Integral: : *specific, finite value, no C *represents total displacement *must be continuous on [a, b]
Trapezoid Rule: w/ n subintervals *width of interval: *subintervals must be equal
Homework Day 1, p. 299: 29 (use left, right, and midpoints with 4 rectangles), 33, 35 Day 2, p. 312: 37-47 odd, 49, 57, 59, 110-113 all