Understanding Definite Integrals in Mathematics
Explore the concept of definite integrals in mathematics, covering properties, solving methods, and applications in finding areas bounded by curves. Prior knowledge of functions, limits, derivatives, and indefinite integrals is essential to grasp this topic effectively. Dive into the unique value of definite integrals, denoted by [a, b], and learn how to calculate it using the limit of a sum or the fundamental theorem of integral calculus. Enhance your problem-solving skills and apply definite integrals to various scenarios to find the bounded area accurately.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
MATHEMATICS : STD. XII Class Topic : DEFINITE INTEGRAL
Learning Objectives STUDENTS WILL BE ABLE TO KNOW Definite integral. Properties of definite integral. To solve definite integral as the limit of a sum. To solve definite integral using fundamental theorem of integral calculus. To solve definite integral using substitution method. Students will be able to solve different types of definite integral problems. They can apply it, to find the area bounded by different curves.
Previous Knowledge STUDENT SHOULD KNOW ABOUT : Functions Limits of a function Derivatives Continuous function Indefinite Integrals
INTRODUCTION Definite Integral: The problem of finding area under a curve with in a limit is called Definite Integral. The definite integral has a unique value. A definite integral is denoted by , where a is called the lower limit of the interval and b is called the upper limit of the interval.
The Definite Integral is introduced in two ways. The Limit of a sum. It has an anti derivative F in the interval [a, b], then its value is the difference between the value of F at the end points i.e. F(b) F(a).
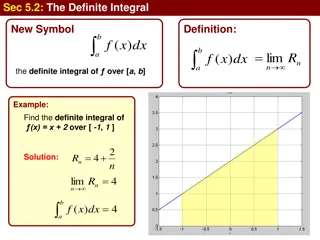
1. Definite Integral as the limit of a sum : Let f be a continuous function defined on closed interval [a, b]. Assume that all the values taken by the function are non-negative, so the graph of the function is a curve above the X-axis.
The Definite integral is the area bounded by the curve y = f(x), the ordinates x = a, x = b and the X-axis. In the figure, Area of the rectangle ABLC Area of region ABDCA Area of the rectangle ABDM. If sn and Sn denote the sum of areas of all lower rectangles and upper rectangles then,
Example: Solution: Here f(x) = x2 + 1 , a = 0 and b = 2, h = 2/n nh = 2. [1 [1 [1 [1 [1 [1
Video Link Activity On Definite Integral https://youtu.be/9lKDEJzgYY8
ASSIGNMENT Evaluate the following definite integrals as limit of sums :
2. Find Definite Integral, using Fundamental Theorem of Integral Calculus. First Fundamental Theorem of Integral Calculus : Let f be a continuous function on the closed interval [a, b] and A(x) be the area function, i.e. A(x) for all x [a, b]. Second Fundamental Theorem of Integral Calculus: Let f be a continuous function defined on the closed interval [a, b] and f be an anti derivatives of f, then,
Example: Evaluate the following integral: Solution:
Evaluation of Definite Integral by Substitution Method: Steps to Evaluate Consider the integral without limits and substitute, y = f(x) or x = g(y) to reduce the given interval to a known form. Integrate the new integrand with respect to the new variable without mentioning the constant of integration. Resubstitute for the new variable and write the answer in terms of the original variable. Find the value of the answers obtained in(3) at the given limits of integral and find the difference of the values at the upper and lower limits.
Example: Evaluate
Example: Evaluate :
Example: Evaluate:
Example: Evaluate
1. 1. is equal to is equal to Example: Evaluate:
Marking Scheme(2 Mark) Q: Evaluate : Solution : We have, Now [1/2 [1/2 [1/2 [1/2
Marking Scheme(4 Mark) Evaluate : Solution : Let [1/2 [using property [1/2 [1/2
[1/2 [1 [1
SUMMARY We discussed the following points :- Introduction of Definite Integral. Definite Integral as limit of sum. Definite integral using Fundamental Theorem of Integral Calculus. Definite Integral by Substitution Method. Properties of Definite Integrals.
MIND MAP DEFINITE INTEGRALS DIRECT PROPERTIES OF DEFINITE INTEGRALS FORMULA FOR LIMIT OF A SUM EVALUATION OF DEFINITE INTEGRALS MODULUS OF A FUNCTION ODD AND EVEN FUNCTION
WORKSHEETS Basic Worksheet Standard Worksheet Advance Worksheet