Reactor Design Equations: Basics and Applications
L2b: Reactor Molar Balance
Example Problems
T
o
d
a
y
w
e
w
i
l
l
u
s
e
B
M
B
t
o
d
e
r
i
v
e
r
e
a
c
t
o
r
d
e
s
i
g
n
e
q
u
a
t
i
o
n
s
.
Y
o
u
r
g
o
a
l
i
s
t
o
l
e
a
r
n
t
h
i
s
p
r
o
c
e
s
s
,
n
o
t
t
o
m
e
m
o
r
i
z
e
t
h
e
e
q
u
a
t
i
o
n
s
!
Review: Basic Molar Balance BMB
System volume
F
j0
F
j
G
j
Rate of flow of
j
into
the system
[moles/time]
Rate of flow of
j
out of
system
[moles/time]
Rate of
generation
of
j
by chemical rxn
[moles/time]
Rate of
accumulation
of
j
in the system
[moles/time]
F
j0
F
j
G
j
-
+
=
Review: Batch Reactor Basic Mole
Balance
•
No material enters or leaves the reactor
•
In ideal reactor, composition and temperature are spatially
uniform (i.e. perfect mixing)
•
No flow in or out of reactor. F
j0
and F
j
= 0.
I
d
e
a
l
(
p
e
r
f
e
c
t
l
y
m
i
x
e
d
)
r
e
a
c
t
o
r
:
s
p
a
t
i
a
l
l
y
u
n
i
f
o
r
m
t
e
m
p
,
c
o
n
c
,
&
r
e
a
c
t
i
o
n
r
a
t
e
Review: CSTR Basic Mole Balance
Accumulation = In - Out + Generation
by rxn
0
= F
j0
- F
j
+
N
o
s
p
a
t
i
a
l
v
a
r
i
a
t
i
o
n
:
•
Continuously add
reactants and remove products
•
In an ideal reactor, composition and temperature
are spatially uniform (i.e. perfect mixing)
•
At steady
state- no accu
mulation
Ideal Steady State CSTR Design Equation:
in terms of
concentration
in terms
of flow
(
u
p
s
i
l
o
n
)
ΔV
F
A0
F
A
Review: Mole Balance – PFR
•
Flow reactor operated at steady
state (no accumulation per
Δ
)
•
Composition of fluid
varies down length of reactor (material
balance for
differential element of volume
V
•
Heterogeneous rxn
: reaction occurs
at catalyst particle surface
•
Concentration gradient of reactant and product change down
length
of the reactor
•
Rxn rate based on the mass of catalyst W, not reactor volume V
Review: Mole Balance- Packed Bed
Reactor (PBR)
Similar to PFR, but expressed in terms of
catalyst weight instead of reactor volume
Units for the rate of a
homogeneous rxn (r
j
) :
U
n
i
t
s
f
o
r
t
h
e
r
a
t
e
o
f
a
c
a
t
a
l
y
t
i
c
r
x
n
(
r
j
’
)
:
So in terms of catalyst weight instead of reactor volume:
Consider a reaction that occurs on a catalyst surface (a
heterogeneous rxn).
How is the reaction rate r’
j
that is in terms of
the weight of catalyst related to the rate in terms of volume (r
j
)?
Hint: r
j
= x r’
j
What is x?
Bulk catalyst
density
r
j
=
b
r’
j
Use your result from the previous question
to derive a reactor design
equation for a fluidized CSTR containing catalyst particles. The equation
should be in terms of catalyst weight (W) and the reaction rate for an
equation that uses solid catalyst. Assume perfect mixing and steady-state
operation of the CSTR.
What is the CSTR design equation?
R
e
a
r
r
a
n
g
e
t
o
p
u
t
i
n
t
e
r
m
s
o
f
V
Use your result from the previous question
to derive a reactor design
equation for a fluidized CSTR containing catalyst particles. The equation
should be in terms of catalyst weight (W) and the reaction rate for an
equation that uses solid catalyst. Assume perfect mixing and steady-state
operation of the CSTR.
Step 1
: Come up with an equation that relates V to W (V=?W) &
substitute this equivalency into the CSTR design equation.
CSTR design equation:
Need an equation that has
W instead of V and –r
j
’
instead of -r
j
S
u
b
s
t
i
t
u
t
e
W
/
ρ
b
f
o
r
V
i
n
d
e
s
i
g
n
e
q
:
S
t
e
p
2
:
S
u
b
s
t
i
t
u
t
e
a
n
e
x
p
r
e
s
s
i
o
n
t
h
a
t
r
e
l
a
t
e
s
–
r
j
t
o
–
r
j
’
i
n
t
o
t
h
e
d
e
s
i
g
n
e
q
:
Simplify:
Ideal Fluidized
CSTR Design
Equation
From the previous question:
r
j
=
b
r’
j
Use basic molar balance
to derive a reactor design equation for a fluidized
CSTR containing catalyst particles. The equation should be in terms of
catalyst weight (W) and the reaction rate for an equation that uses solid
catalyst. Assume perfect mixing and steady-state operation of the CSTR.
1.
S
i
m
p
l
i
f
y
t
h
i
s
e
x
p
r
e
s
s
i
o
n
.
T
h
i
n
g
s
t
o
c
o
n
s
i
d
e
r
:
I
s
t
h
e
r
e
f
l
o
w
?
A
c
c
u
m
u
l
a
t
i
o
n
?
I
s
t
h
e
r
e
a
c
t
i
o
n
r
a
t
e
t
h
e
s
a
m
e
e
v
e
r
y
w
h
e
r
e
i
n
t
h
e
r
e
a
c
t
o
r
?
0
At steady state
Rearrange to get in terms of W
Ideal Fluidized
CSTR Design
Equation
The reaction A→B is to be carried out isothermally in a continuous-flow
reactor. Calculate the
CSTR
volume to consume 99% of A (
C
A
=
0.01C
A0
)
when the
entering molar flow rate is 5 mol A/h
, the
volumetric flow rate is
constant at 10 dm
3
/h
and the rate is
–r
A
=
(3dm
3
/mol•h)C
A
2
.
0
=
10 dm
3
/h
=
CSTR design eq:
Substitute in:
–r
A
=
(3dm
3
/mol•h)C
A
2
&
C
A
=
0.01C
A0
W
e
k
n
o
w
.
W
h
a
t
i
s
C
A
0
?
The reaction A→B is to be carried out isothermally in a continuous-flow
reactor. Calculate the
PFR
volume to consume 99% of A (C
A
=0.01C
A0
)
when the entering molar flow rate is 5 mol A/h, the volumetric flow rate is
constant at 10 dm
3
/h and the rate is
–r
A
=
(3dm
3
/mol•h)C
A
2
.
0
=
10 dm
3
/h
=
PFR design eq:
Substitute in:
–r
A
=(3dm
3
/mol•h)C
A
2
but
not C
A
=0.01C
A0
until after integration
!
M
u
c
h
s
m
a
l
l
e
r
V
r
e
q
u
i
r
e
d
t
o
g
e
t
s
a
m
e
c
o
n
v
e
r
s
i
o
n
i
n
a
P
F
R
t
h
a
n
i
n
a
C
S
T
R
R
E
V
I
E
W
:
for n≠1:
The gas phase reaction A→B+C will be carried out isothermally in a 20 dm
3
constant volume, well-mixed batch reactor.
20 moles of pure A
is initially
placed in the reactor. If the rate is
–r
A
=
kC
A
and
k
=
0.865 min
-1
, calculate the
time needed to reduce the number of moles of A in the reactor to
0.2 mol
.
DDDD
N
e
e
d
t
o
c
o
n
v
e
r
t
t
o
d
C
A
/
d
t
H
o
w
i
s
d
C
A
/
d
t
r
e
l
a
t
e
d
t
o
d
N
A
/
d
t
?
0
P
l
u
g
i
n
t
o
d
e
s
i
g
n
e
q
P
l
u
g
i
n
r
a
t
e
l
a
w
R
e
a
r
r
a
n
g
e
&
i
n
t
e
g
r
a
t
e
C
o
n
v
e
r
t
C
j
b
a
c
k
t
o
N
j
/
V
S
u
b
s
t
i
t
u
t
e
i
n
v
a
l
u
e
s
f
o
r
k
,
N
A
0
,
&
N
A
0
0
R
E
V
I
E
W
:
for n=1:
There are initially 500 rabbits (x) and 200 foxes (y). Use Polymath to plot the
number of rabbits and foxes as a function of time for a period of up to 500 days.
The predator-prey relationship is given by the following coupled ODEs:
Constant for growth for rabbits k
1
= 0.02 day
-1
Constant for death of rabbits k
2
=0.00004/(day
∙number of foxes)
Constant for growth of foxes after eating rabbits
k
3
=0.0004/(day
∙number of rabbits)
Constant for death of foxes
k
4
= 0.04 day
-1
Also, what happens if k
3
=0.00004/day and t=800 days? Plot the number of foxes vs
rabbits.
Polymath example problem 1-17
•
Make sure the “Graph” and “Report” buttons are checked above
•
After typing in the 2 differential equations, conditions for t=0, constants,
and initial and final time pts, press the magenta arrow to solve
Initially 500 rabbits (x) and 200 foxes (y). Predator-prey relationship is given by the
following coupled ODEs:
Constant for growth of rabbits: k
1
= 0.02 day
-1
Constant for death of rabbits: k
2
=0.00004/(day
∙number of foxes)
Constant for growth of foxes after eating rabbits
k
3
=0.0004/(day
∙number of rabbits)
Constant for death of foxes
k
4
= 0.04 day
-1
t= 0 to 500 days
Polymath report:
Number of rabbits at
500 days
Number of foxes at
500 days
Polymath graph:
What happens if k
3
=0.00004/day and t=800
days? Plot the number of foxes vs rabbits.
•
Make sure the “Graph” and “Report” buttons are checked above
•
After changing t(f) to 800 and k3 to 0.00004, press the magenta arrow
to solve
Number of rabbits
at 800 days
Number of foxes at
800 days
This material covers the foundational concepts of reactor design equations, focusing on molar balance in batch reactors, continuous stirred tank reactors (CSTRs), and plug flow reactors (PFRs). Through detailed explanations and illustrative examples, you will gain a comprehensive understanding of how to derive and apply these equations in the context of chemical reactions. Emphasizing learning the process over memorization, these slides provide a valuable resource for chemical engineering students and professionals.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
L2b: Reactor Molar Balance Example Problems L2b-1 Fj0 Fj Gj reactor Today we will use BMB to derive reactor design equations. Your goal is to learn this process, not to memorize the equations! Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L2b-2 Review: Basic Molar Balance BMB Rate of generation of j by chemical rxn [moles/time] Rate of Rate of flow of j into the system [moles/time] Rate of flow of j out of system [moles/time] accumulation of j in the system [moles/time] - + = dN dt j Fj0 Fj Gj V jr dV Fj0 Fj Gj System volume Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
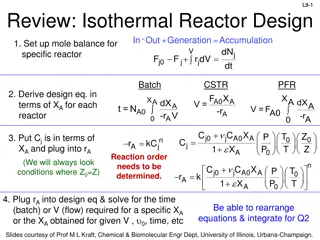
Review: Batch Reactor Basic Mole Balance No material enters or leaves the reactor In ideal reactor, composition and temperature are spatially uniform (i.e. perfect mixing) No flow in or out of reactor. Fj0 and Fj = 0. L2b-3 Rate of generation of reactant A in reactor due to rxn Rate of accumulation of reactant A in reactor = V dN j Batch Reactor Design Equation = r dV j dt Ideal (perfectly mixed) reactor: spatially uniform temp, conc, & reaction rate dN Ideal Batch Reactor Design Equation j = r V j dt Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L2b-4 Review: CSTR Basic Mole Balance Continuously add reactants and remove products In an ideal reactor, composition and temperature are spatially uniform (i.e. perfect mixing) At steady state- no accumulation Fj0 Fj Accumulation = In - Out + Generation by rxn 0 = Fj0 - Fj + V r jdV No spatial variation: rj V Ideal Steady State CSTR Design Equation: F F r C C ( )( ) j j in terms of flow in terms of concentration 0 A A 0 0 V F C V = = = j j r j A (upsilon) Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L2b-5 Review: Mole Balance PFR Flow reactor operated at steady state (no accumulation per ) Composition of fluid varies down length of reactor (material balance for differential element of volume V V FA0 FA dNj rj V - + = Fj0 Fj dt F F lim + j V V V j V = r + = F F r V 0 j j j j V 0 + V V V dF Ideal SS PFR Design Eq. j = r j dV Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
Review: Mole Balance- Packed Bed Reactor (PBR) L2b-6 Heterogeneous rxn: reaction occurs at catalyst particle surface Concentration gradient of reactant and product change down length of the reactor Rxn rate based on the mass of catalyst W, not reactor volume V dF Similar to PFR, but expressed in terms of catalyst weight instead of reactor volume j = r j dV mol mol Units for the rate of a homogeneous rxn (rj) : Units for the rate of a catalytic rxn (rj ) : 3 s m s catalyst kg So in terms of catalyst weight instead of reactor volume: dF j j= where ' r W weight the is of catalyst the dW Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L2b-7 Consider a reaction that occurs on a catalyst surface (a heterogeneous rxn). How is the reaction rate r j that is in terms of the weight of catalyst related to the rate in terms of volume (rj)? Hint: rj = x r jWhat is x? mol mol Rearrange to solve for x = x 3 s catalyst kg s m mol s catalyst kg = x 3 mol s m catalyst kg catalyst weight Bulk catalyst density = = = x b 3 catalyst volume m rj = br j Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L2b-8 Use your result from the previous question to derive a reactor design equation for a fluidized CSTR containing catalyst particles. The equation should be in terms of catalyst weight (W) and the reaction rate for an equation that uses solid catalyst. Assume perfect mixing and steady-state operation of the CSTR. What is the CSTR design equation? In Out - + Gen = Accumulation dN dt 0 j F F r V 0 + = j j j Rearrange to put in terms of V F F j0 j = V r j Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L2b-9 Use your result from the previous question to derive a reactor design equation for a fluidized CSTR containing catalyst particles. The equation should be in terms of catalyst weight (W) and the reaction rate for an equation that uses solid catalyst. Assume perfect mixing and steady-state operation of the CSTR. CSTR design equation: V = Need an equation that has W instead of V and rj instead of -rj F F j0 j r j Step 1: Come up with an equation that relates V to W (V=?W) & substitute this equivalency into the CSTR design equation. W V b F F F F W W j0 j Substitute W/ b for V in design eq: j0 j = = = V V = r b r b j j Step 2: Substitute an expression that relates rj to rj into the design eq: mol s m From the previous question: rj = br j mol Units for rj: Units for rj : s kg catalyst 3 F F F F Ideal Fluidized CSTR Design Equation F F W W j0 j j0 j j0 j = = = W Simplify: ( ) r r ' r ' b j b j b j Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L2b-10 Use basic molar balance to derive a reactor design equation for a fluidized CSTR containing catalyst particles. The equation should be in terms of catalyst weight (W) and the reaction rate for an equation that uses solid catalyst. Assume perfect mixing and steady-state operation of the CSTR. In Out - +Generation = Accumulation W j0 j j F F r 'dW + dN dt d dt j = mol s mol s mol kg s ( ) ( ) kg mol 1. Simplify this expression. Things to consider: Is there flow? Accumulation? Is the reaction rate the same everywhere in the reactor? dN dt W j At steady state + = F F r 'dW j0 j j 0 Rearrange to get in terms of W r 'W + = F F 0 j0 j j Ideal Fluidized CSTR Design Equation F F j0 j = = F F r 'W W j0 j j r ' j Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L2b-11 The reaction A B is to be carried out isothermally in a continuous-flow reactor. Calculate the CSTR volume to consume 99% of A (CA=0.01CA0) when the entering molar flow rate is 5 mol A/h, the volumetric flow rate is constant at 10 dm3/h and the rate is rA=(3dm3/mol h)CA2. 0 = 10 dm3/h = reactor FA0=5 mol A/h ( )( ) = jF C j FA= CA where CA = 0.01CA0 dN dt j CSTR design eq: In Out - F F r V + Gen = Accumulation 0 + = j j j 0 C C F F Substitute in: rA=(3dm3/mol h)CA2 & CA=0.01CA0 A0 A A 0 A = = V V r r A A ( ) 2 1 0.01 C C 0.01C A0 A0 3 A 0 Factor numerator = = V V ( )( ( )( 2 ) ) 2 3 2 3dm mol h 0.01 C 3dm mol h 0.01 C A0 A0 mol 0.99 5 F mol dm We know . What is CA0? ) ) ( h= V= A 0 = ( )( C = 0 .5 C 2 A0 ) A0 3 3 3 3dm mol h 0.01 C ( 10dm h A0 0 3 0.99 10 dm h = 3 V = V 66,000 dm ( )( ) 2 3 3 3dm mol h 0.01 0.5 mo l d m Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L2b-12 The reaction A B is to be carried out isothermally in a continuous-flow reactor. Calculate the PFR volume to consume 99% of A (CA=0.01CA0) when the entering molar flow rate is 5 mol A/h, the volumetric flow rate is constant at 10 dm3/h and the rate is rA=(3dm3/mol h)CA2. 0 = 10 dm3/h = ( j C 5mo l h mol dm C = = 5 0 . A0 )( ) 3 3 10dm h = jF reactor FA= CA where CA = 0.01CA0 FA0=5 mol A/h dF dV d C Substitute in: rA=(3dm3/mol h)CA2but not CA=0.01CA0 until after integration! A V PFR design eq: = A r = r A A d 0 .01C 3 V dC C dC dV A0 dm mol h A 2 2 A = dV = 3 C ( ) A 3 3dm mol h C 0 A A0 b ) ( ( b b b b n 1 + n 1 + 1dx x dx x 1 b + a + REVIEW: for n 1: ) n 1 + n x n 1 + = x dx = 2 x n n 1 n 1 a a a a a 3 3 10dm dm 3 h 1 1 dm 1 C 1 = V = V ( ) ( ) 3 0. 01 0. 5 0.5 m ol 3 0.01 C 3dm mol h A0 A0 mol h Much smaller V required to get same conversion in a PFR than in a CSTR 3 = 660 dm V Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L2b-13 The gas phase reaction A B+C will be carried out isothermally in a 20 dm3 constant volume, well-mixed batch reactor. 20 moles of pure A is initially placed in the reactor. If the rate is rA=kCA and k=0.865 min-1, calculate the time needed to reduce the number of moles of A in the reactor to 0.2 mol. DDDD 0 j j j In Out 0 0 dN dt dN dt Batch reactor design eq j A F F r V = + = r V +Gen=Accum - A N Need to convert to dCA/dt How is dCA/dt related to dNA/dt? d V dt dt dC V dt b 1dx x A = = C so N C V A A A V d N d C d d d V t d N d N d C Plug into design eq ( ) A A t A A A t = + = = V C C V A A dt dt d 0 dC d ( ) ln x dC dt Plug in rate law Rearrange & integrate A A t A = = = r V r k C A A A b a lnb REVIEW: for n=1: ( ) ( ) = ln b ln a = = a n a lnC C N N 1 k C N N V V t dC C Convert Cj back to Nj/V A A A A = = kt t ln = A kt ln = k dt A0 A0 A0 A 0 C A 0 min 0.86 ln0. 2 = t 0 = t 5.3 min Substitute in values for k, NA0, & NA 5 2 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L2b-14 Polymath example problem 1-17 There are initially 500 rabbits (x) and 200 foxes (y). Use Polymath to plot the number of rabbits and foxes as a function of time for a period of up to 500 days. The predator-prey relationship is given by the following coupled ODEs: dy dx = k xy k y = 1 k x k xy 3 4 2 dt dt Constant for growth for rabbits k1= 0.02 day-1 Constant for death of rabbits k2=0.00004/(day number of foxes) Constant for growth of foxes after eating rabbits k3=0.0004/(day number of rabbits) Constant for death of foxes k4= 0.04 day-1 Also, what happens if k3=0.00004/day and t=800 days? Plot the number of foxes vs rabbits. Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L2b-15 Initially 500 rabbits (x) and 200 foxes (y). Predator-prey relationship is given by the following coupled ODEs: xy k x k dt Constant for growth of rabbits: k1= 0.02 day-1 Constant for death of rabbits: k2=0.00004/(day number of foxes) Constant for growth of foxes after eating rabbits k3=0.0004/(day number of rabbits) Constant for death of foxes k4= 0.04 day-1 t= 0 to 500 days dx dy = 1 = k xy k y 2 3 4 dt Make sure the Graph and Report buttons are checked above After typing in the 2 differential equations, conditions for t=0, constants, and initial and final time pts, press the magenta arrow to solve Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L2b-16 Polymath report: Number of rabbits at 500 days Number of foxes at 500 days Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L2b-17 Polymath graph: Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L2b-18 What happens if k3=0.00004/day and t=800 days? Plot the number of foxes vs rabbits. Make sure the Graph and Report buttons are checked above After changing t(f) to 800 and k3 to 0.00004, press the magenta arrow to solve Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L2b-19 Number of rabbits at 800 days Number of foxes at 800 days Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
L2b-20 Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois at Urbana-Champaign.
