12.3 Tangent to a Curve

Concept of tangents to curves and derivatives by examining lines tangent to a curve at a point, finding slopes, equations of tangent lines, and the first derivative of a function. Understand how to calculate the slope and equation of a tangent line for a given function at a specific point. Dive into the mathematical principles behind tangents and derivatives to enhance your problem-solving skills.

• Tangents
• Curves
• Derivatives
• Slope Calculation
• Equations

nakagawa_a Follow

Uploaded on Feb 23, 2025 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

1. 12.3 Tangent to a Curve

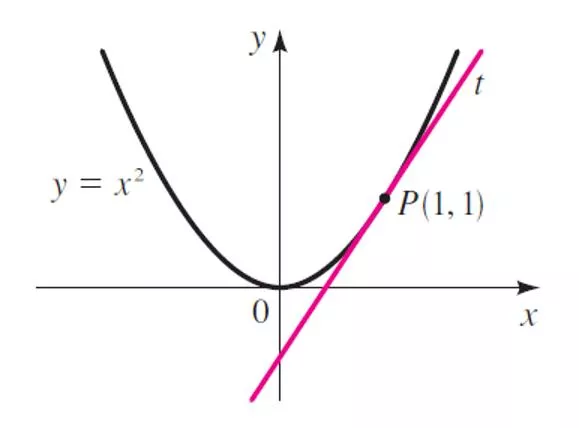
2. A line tangent to a curve is the line that passes through the point and that has a slope that is the same as the slope of the curve at that point.

3. Let A and B be two points near each other on the curve and let the coordinates of A be (x, f(x)). Suppose the x-coordinate of B differs from the x- coordinate of A by a small amount, h. Then the coordinates of B are (x + h, f(x + h)) What is the slope of the line? ( ) ( ) f x x ( ) ( ), + + f x h f x h f x = 0 h + x h h

4. Suppose A remains fixed while B moves a long the curve toward A. Then the value of h will become smaller, approaching zero. Thus, h can be considered as a variable that approaches zero as B approaches A. If B is made to coincide with A, then the secant line becomes tangent to the curve at point A. tangent secant ( ) ( ) f x + f x h lim h h 0

5. Find the slope of a line tangent to y = 2x2 3x + 1 ( ) ( ) lim h h ( ) ( ) 2 3 lim h h ( 2 2 3 lim h + f x h f x = 4 3 m x 0 ( ) 2 + + + + 2 1 2 3 1 x h x h x x 0 ) + + 1 2 + + 2 2 2 3 3 1 x xh h x h x x h 0 + 2 4 2 h 3 + + xh h h 2 2 2 2 4 2 h 3 2 x xh h h x = lim h lim h 0 0 ( ) = = + 4 3 x lim 4 h 2 3 x h 0

6. The first derivative (f(x)) of a function tells you the slope of all lines tangent to the function and is defined as: + ( ) ( ) f x f x h = '( ) f x lim h h 0

7. Find the equation of the line tangent to the graph at the indicated point: y = x2+ x 1 at (-4, 11) ( ) ( ) lim h h ( ) ( ) ( 1 lim h h 2 1 lim h h 2 2 lim h h ( ) ( ) ' 2 4 1 f x = + ( ) ' 7 f x = + = + + f x h f x y mx b ( 7 = 28 b = b = ) + 11 11 17 4 b 0 ) 2 + + + + 2 1 x h x h x x 0 = 7 17 y x + + + + + 2 2 2 1 x xh h x h x x 0 + + xh h h ( ) = + + = + lim 2 h 1 x h 2 1 x 0 0

8. Find the equation of the line tangent to the graph at the indicated point: 4 at (4, 1) y x ( ) ( ) lim h h 4 4 x h x h 0 h h 4 lim h x x h + 4 lim h x x h + 4 4 1 4 = ( ) ' 4 = = = f ( ) 4 2 16 + f x h f x = = + y 1 mx b ( ) 4 1 b = + b = 0 1 4 4 4 x x + h + 4 b ( ) x x h + lim h = lim 1 2 0 1 h h 1 4 ( ) = + 2 y x 0 4 x = ( ) 2 0

9. Find the derivative of the function f(x) = 8x2+ 2x 4 at x = 2. ( ) ( ) f x h f x h ( ) ( ) 8 2 4 x h x h h 2 2 8 16 8 2 x xh h x h 2 16 8 2 xh h h h ( ) 0 + lim h 0 ( ) 2 + + + + 2 8 2 4 x x lim h 0 + + + + 4 8 + 2 2 2 4 h x x lim h 0 ( ) ' 2 ( ) ' 2 ( ) = = + 16 2 34 2 f f + + lim h 0 ( ) + + = + lim 16 h 8 2 16 2 x h x

10. 12.3 b Derivatives Who uses this? Quantitative Analyst Financial Engineer Fund Accountant Engineering Researcher

11. The derivative of a function f(x) is another function f (x), that gives the slope of the tangent line to the function at any point. + ( ) ( ) f x f x h = '( ) f x lim h h 0

12. The process of finding the derivative is called differentiation. (this is one of the main parts of Calculus) Another common notation for dy '( ) is , ' dx This notation emphasizes that the derivative is a limit of slope, which is a change in y divided by a change in x. f x y

13. Ex 1 Find an expression for the slope of the tangent line to the graph of y = 2x2 3x + 4 at any point. = = ' 4 3 m y x Find the slopes of the tangent lines when x = -1 and x = 5. ( ) ( ) ' 1 4 1 3 7 y = = ( ) ' 5 ( ) 4 5 = 3 17 = y

14. Rules: 1. Constant: f(x) = constant f (x) = 0 if f(x) = xn(n is a rational #) then f (x) = nxn 1 2. Power: EX 2 f(x) = x3 ( ) ' f ( ) ' f 3 1 = = 3 3 x x x x 2

15. 3. Product of Constant & Power: f(x) = cxn then f (x) = cnxn - 1 EX 3: f(x) = 4x2 ( ) ' f x = 8 x 4. Sum & Difference: if f(x) = g(x) +/- h(x) then f (x)=g (x) +/- h (x) EX 4: f(x) = x3+ 5x2+ 6 ( ) ' 3 f x = + + = + 2 2 10 0 3 10 x x x x

16. 5. Product: ( dx ) means the derivative of u times v both d uv which are written in terms of x. d(uv) dx dx v u v v + = v du u dv dx What does this mean? Derivative of the first factor times the second factor plus the first factor times the derivative of the second factor. = + du ' ' u dx

17. = ' 2 2 u v = x = = + 2 3 7 u v x 2 Ex 5 ' x f(x) = (x2 + 3)(2x 7) ( ) ( 2 ' f x = ( ) ' 4 f x x = ( ) ' 6 f x x = ( ) ( ) 2 ) ( ) + + 2 x 3 x x 2 7 + + + 2 2 14 14 2 6 6 x x x 2 = = 2 + 2 ' 1 u = ' v = 1 u v x x 2 2 2 2 x x f(x)=(x + 1)(x2 2x) ( ) ( ) 1 ' f x = ( ) ' f x = ( ) ' f x = ( ) ( + ( x ) 1 ) + + x + x 2 x 2 2 x 2 x 2 2 2 2 2 2 x 3 x 2 x 2 x x

18. = u v v du dx u dv dx 6. Quotient: d 2 dx v u v ' ' u v u v = d 2 v x = 6: ( ) f x EX 1 x ( )( 1 ) ( )( ) ) 1 1 1 1 1 1 x x x x ( ) x = = = ' f ( ) ( ) 2 ( 2 2 x 1 x x

19. + 2 2 5 3 x x x = 7: ( ) f x EX 3 ( ) ( ) ) 5x x ( 2 x ( 5x x ) ( x 3 2 + 2 15 1 3 4 x ( ) x = ' f ) 2 3 = 3 5 v x x = ' + 2 2 3 u u x = ' 15 = 4 x 2 1 v x

20. ( ) + 2 3 7 3 1 2 x x = 8: ( ) f x EX 2 x x ( ) ( ) ( ) ( ) ) 2 3 + 2 6 x+ 7 1 x x 4 2 ( 3 2 x x + 3 2 x x 2 35 3 x x ( ) x = ' f 2 2 ( ) = = + + 2 3 2 v x x = ' 14 = ( ) ( x x 35 x 2 3 7 1 u u x x + )( ) 3 2 2 7 1 3 x x ' 6 2 v x = 4 2 ' 3 u x

21. 7. Power of a Polynomial (The Chain Rule): ( ) d u dx ( ) ( ) ( ) ( ) ' ' x n u u = n du dx = 1 n nu n = f x u 1 n f EX 9: f(x)=(3x 4)3 ( ) ' f x ( ) ' f x ( ( ) ( ) ) 2 = 3 3 4 3 x 2 = 9 3 4 x

22. ( ) ( f x )( ) 2 = + 3 4 3 7 2 5 x x x Ex 10 ( ) 2 = = + x 4 = ' 2 2 2 2 5 + 3 v v x ( 3 = 7 u x 9 x 7 ) 1 u x 4 3 ' 5 8 x ( ) ( ) ( ) ( ) ( x ) 2 x + + x + 4 3 3 4 = 2 5 2 3 7 16 2 5 x x x ' 9 7 f x

23. = 2 Ex 11 ( ) f x 1 x 1 2 ( ) ( f x ) = 2 1 x 1 2 1 2 ( ) ( 1 ( ) x ) = 2 ' 2 f x x x ( ) x = ' f 1 2 ( ) 2 1 x x ( ) x = ' f 2 1 x

24. = = = = ' ' 2 3 u v x ( 2 u v x ( 2 x ( ) f x = Ex 12 ) ( ) ) 3 2 3 + 2 1 x + 2 + 1 2 2 x x 1 x ( ) ( ) 3 2 x + x x + 2 2 2x 1 6 ) 1 2x ( x + ( ) x = ' f 6 2 1 ( ) ( )( f x = ) 3 + 2 2 1 x x )( ) ( ) x ( ) ( 1 3 4 ( ) ( x ) = + + 3 x + 2 2 2 ' 2 1 2 f x x x 3 2 6 + x + x ( ) x = + ' f ( ) ( ) 3 4 2 2 1 1 x x

25. WS 12.3