Understanding Conditional Probability and Bayes Theorem
Conditional probability relates the likelihood of an event to the occurrence of another event. Theorems such as the Multiplication Theorem and Bayes Theorem provide a framework to calculate probabilities based on prior information. Conditional probability is used to analyze scenarios like the relati
1 views • 5 slides
Exploring Interior and Exterior Angles of Triangles
Discover the world of interior and exterior angles of triangles through engaging activities and visual aids. Learn how to calculate the angles, understand the Triangle Sum Theorem, and master the concept of remote exterior angles. Get ready to sharpen your geometry skills with practical examples and
0 views • 28 slides
SUD Life Century Gold - Individual Saving Life Insurance Plan
SUD Life Century Gold is a Non-Linked, Non-Participating Individual Savings Life Insurance Plan offering flexibility in policy and premium paying terms. It provides two plan options - Goal Sure and Edu Sure, with guaranteed additions and tax benefits under Section 80C and Section 10(10D) of The Inco
0 views • 13 slides
Solving for Midsegment Length in Isosceles Triangle
The Rock and Roll Hall of Fame triangular face in Cleveland is an isosceles triangle with a base length of 229 ft. 6 in. By using the midsegment theorem, we can find the length of the highlighted line at the halfway point of both legs of the triangle. This involves connecting the midpoints of two si
0 views • 13 slides
Biometrical Techniques in Animal Breeding: Analysis of Variance in Completely Randomized Design
Biometrical techniques in animal breeding involve the use of analysis of variance (ANOVA) to partition total variance into different components attributable to various factors. In completely randomized designs, experimental units are randomly assigned to treatments, ensuring homogeneity. The total n
0 views • 34 slides
Understanding the Coase Theorem: Property Rights and Economic Efficiency
The Coase Theorem, developed by economist Ronald Coase, posits that under certain conditions, bargaining related to property rights will lead to an optimal outcome regardless of the initial distribution. It provides a framework for resolving conflicts by emphasizing negotiation and efficient market
0 views • 10 slides
Understanding the Binomial Theorem
An explanation of binomials, Pascal's Triangle, and the Binomial Theorem with examples and applications in algebra. Special cases and series expansions are covered, providing insights into the manipulation of binomial expressions for various powers and applications. The content illustrates the expan
1 views • 8 slides
Understanding Binomial Theorem in Mathematics
Explore the Binomial Theorem in mathematics, covering Pascal's Triangle, binomial expansions, coefficients, general terms, and more. Learn how to expand binomials, analyze powers, find approximate numbers, and determine middle terms. Discover the structure of Pascal's Triangle and apply it to expand
0 views • 37 slides
Understanding the Pythagorean Theorem and Right-Angled Triangles
Explore the Pythagorean Theorem, which states that in a right-angled triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the other two sides (a and b). Learn how to identify the hypotenuse, use the theorem to find missing lengths, and visually understand th
1 views • 25 slides
Engineering Mechanics: Lami's Theorem and Cylinder Reactions Problem
This course material covers Lami's Theorem in Engineering Mechanics taught by Ranbir Mukhya. It includes an outline of the theorem, problem scenarios involving cylinders with given weights and diameters, and the determination of reactions at various points. Detailed force diagrams and calculations a
0 views • 8 slides
Insights into the Mean Value Theorem and Its Applications
Delve into the Mean Value Theorem (MVT) with a focus on concepts like Lagrange's MVT, Rolle's Theorem, and the physical and geometrical interpretations. Explore the conditions, statements, and special cases of MVT, along with practical applications and geometric insights. Dr. Arnab Gupta, an Assista
0 views • 14 slides
Understanding the Residue Theorem in Complex Analysis
The Residue Theorem is a powerful tool in complex analysis that allows us to evaluate line integrals around paths enclosing isolated singularities. By expanding the function in a Laurent series, deforming the contour, and summing residues, we can evaluate these integrals efficiently. This theorem ex
0 views • 31 slides
Understanding Superposition Theorem in Electrical Circuits
Superposition theorem in electrical circuits states that the effects of multiple voltage and current sources in a network can be analyzed independently and then combined algebraically. This allows for calculating the voltage and current distribution in a network more efficiently. The theorem involve
0 views • 9 slides
Understanding Lami's Theorem in Physics
Lami's Theorem is an equation that explains how the magnitudes of forces acting on a point keep an object in equilibrium. This theorem relates the forces with corresponding angles and is derived by understanding the sum of forces acting on a point. By utilizing complementary angles and the sine rule
0 views • 8 slides
Exploring the Pythagorean Theorem and Its Origins
The Pythagorean Theorem, named after the ancient Greek mathematician Pythagoras, is a fundamental principle in geometry relating to right triangles. While Pythagoras is credited with offering a proof of the theorem, evidence suggests that earlier civilizations like the Babylonians and ancient Chines
0 views • 21 slides
Optical Alignment Using Beam Triangle Opti 521 Phil Scott
This presentation delves into the intricate process of optical alignment using a beam triangle, focusing on defining optical and mechanical axes, addressing alignment challenges, degrees of freedom for various elements, and the importance of setting up a beam triangle for accurate alignment. The con
0 views • 14 slides
Solving Maximum Contiguous Subarray Sum Problem with Dynamic Programming
Explore the concept of finding the maximum contiguous subarray sum using dynamic programming as an improvement over divide and conquer algorithms. Learn the steps of defining the objective, writing recurrences, designing memoization structures, and implementing iterative algorithms. Delve into the d
1 views • 32 slides
Understanding Bayes Theorem in NLP: Examples and Applications
Introduction to Bayes Theorem in Natural Language Processing (NLP) with detailed examples and applications. Explains how Bayes Theorem is used to calculate probabilities in diagnostic tests and to analyze various scenarios such as disease prediction and feature identification. Covers the concept of
0 views • 13 slides
Exploring Pythagoras Theorem: Making a 3:4:5 String Triangle
Explore Pythagoras theorem by creating a 3:4:5 string triangle to test object alignment. Learn about Pythagoras, his theorem, and how it applies to right-angled triangles. Follow step-by-step instructions with images for a safe hands-on activity. Discover the significance of the 3:4:5 triangle and i
0 views • 15 slides
Triangle Partitioning and Linear Optimization in Hockey Line Analysis
In this presentation, the speaker discusses the use of triangle partitioning and linear optimization techniques to analyze hockey team lines. The goal is to find chemistry between players, allocate ice time effectively, and match up against opposing lines for a better chance of winning games. Tradit
0 views • 16 slides
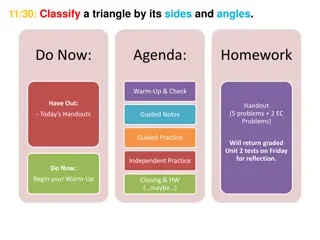
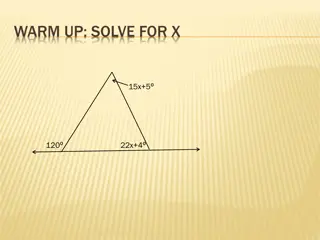
Understanding Triangle Classification: Sides and Angles
Explore how to classify triangles based on their sides and angles, using the Triangle Sum Theorem and linear pair theorem to find missing angle measures. Learn to distinguish between different types of triangles such as right, isosceles, equilateral, and obtuse, and solve problems involving properti
0 views • 13 slides
Problem Solving with Pythagoras Theorem in Geometry
Explore the application of Pythagoras Theorem in solving problems related to right-angled triangles, diagonals of shapes like rectangles and rhombuses, and the height of triangles. Learn how to use Pythagoras Theorem effectively by drawing diagrams, identifying known lengths, and using the theorem t
0 views • 8 slides
Understanding Triangle Properties in Geometry
Explore the classification of triangles based on sides and angles, learn about the Triangle Sum Property, Exterior Angle Theorem, and Corollary to the Triangle Sum Theorem. Dive into examples and concepts to deepen your grasp of congruent triangles in geometry.
0 views • 68 slides
Understanding Triangles: Classifying by Sides and Angles
Delve into the world of triangles in geometry with a focus on classifying them by their sides and angles. Learn about equilateral, scalene, and isosceles triangles based on side lengths, and explore equiangular, right, acute, and obtuse triangles according to angle measurements. Uncover the Triangle
0 views • 60 slides
Mastering Line and Triangle Geometry: Rules and Angle Calculations
Revisit the main rules and terms of line and triangle geometry to calculate angles. Understand types of angles, such as right, acute, obtuse, and reflex. Learn about various angle rules like angles on a straight line, angles at a point, vertically opposite angles, angles in a triangle, equilateral t
0 views • 46 slides
Exploring Pythagoras Theorem in Triangles
Delve into the fascinating world of Pythagoras Theorem and its application in right-angled triangles. Uncover the historical significance of this mathematical concept, engage in practical activities to understand its principles, and discover the connection between the squares of the triangle's sides
0 views • 14 slides
Modification of Nucleon Spectral Function in Nuclear Medium from QCD Sum Rules
Investigating the modification of nucleon properties in the nuclear medium using QCD sum rules, focusing on hadron properties, mass spectrum, and chiral symmetry restoration. The study discusses the mass differences, non-perturbative contributions, and the analysis of QCD sum rule in nuclear matter.
0 views • 27 slides
Faster Space-Efficient Algorithms for Subset Sum
This research discusses faster and space-efficient algorithms for Subset Sum and related problems, introducing techniques like Meet-in-the-Middle (MitM) approach and Monte Carlo algorithm. It also covers topics such as Floyds Cycle Finding, Element Distinctness (ED) by BCM, List Disjointness, and Su
0 views • 25 slides
Understanding Polygons in Geometry
Explore the concept of polygons, their sides, vertices, and angles, and learn to classify them as convex or concave. Discover the Polygon Angle Sum Theorem and find the sum of measures of angles in a given polygon.
0 views • 13 slides
Understanding Data Structures in Triangle Meshes
Delve into the data structure of triangle meshes, as explained by Yutaka Ohtake from the Department of Precision Engineering at the University of Tokyo. Explore adjacent vertex and face lists, as well as the construction algorithms for creating these lists. Learn about the implementation methods, la
0 views • 24 slides
Understanding Calculus: From MVT to FTC with Lin McMullin
Join Lin McMullin in exploring the transition from the Mean Value Theorem (MVT) to the Fundamental Theorem of Calculus (FTC). Discover the significance of MVT, Fermat's Theorem, Rolle's Theorem, and the Mean Value Theorem, all crucial concepts in calculus. Engage in graphical explorations, proving m
0 views • 45 slides
Understanding Rolle's Theorem and The Mean Value Theorem in Calculus
Rolle's Theorem states that for a continuous and differentiable function on a closed interval with equal function values at the endpoints, there exists at least one point where the derivative is zero. The Mean Value Theorem asserts that for a continuous and differentiable function on an interval, th
0 views • 5 slides
Introduction to Analysis: Mean Value Theorem and Related Theorems
This resource delves into key concepts such as the Mean Value Theorem, Fermat's Theorem, Rolle's Theorem, Extreme Value Theorem, local maximums, and more. It presents important results and explores proofs in the context of analysis.
0 views • 71 slides
Introduction to Applying Pythagorean Theorem in Right Triangles
In this lesson, we will learn how to apply the Pythagorean Theorem to find missing side lengths of right triangles. The Pythagorean Theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Through examples and practice problems,
0 views • 13 slides
Understanding Polygon Angle-Sum Theorems
Explore the Polygon Angle-Sum Theorems that determine the sum of interior angle measures in polygons. Learn about the Polygon Angle-Sum Theorem, number of sides in polygons, finding angle sums, and the corollary for regular polygons. Practice using the theorems to calculate interior angle measures i
0 views • 18 slides
Geometry Fundamentals: Theorems and Concepts Explained
Explore essential concepts in geometry such as solving equations, perpendicular transversal theorem, triangle exterior angle theorem, angle sum theorems, polygon classification, and naming polygorgons. Learn about the interior and exterior angles of triangles and why they add up to specific measurem
0 views • 21 slides
Understanding Binomial Theorem: Expansion, Examples, and Applications
Binomial theorem is a powerful mathematical concept used to expand expressions involving binomials. This presentation explores the basics of binomial expansion, formulae for positive, negative, and fractional indices, along with examples demonstrating its application. By leveraging the binomial theo
0 views • 10 slides
Understanding Automated Theorem Proving in Lean
Dive into the world of automated theorem proving in Lean with a focus on formal verification, history, and the use of logic and computational methods. Explore how programs can assist in finding and verifying proofs, as well as the significance of interactive theorem provers. Discover the evolution o
0 views • 35 slides
Efficient Parallel Triangle Listing on Batch-Dynamic Graphs
Efficiently listing triangles in dynamic graphs is essential for identifying dense subgraphs in social networks. This study focuses on fast triangle listing in large graphs, particularly after batch updates, to find new and deleted triangles. The problem statement involves listing all triangles from
0 views • 27 slides
Triangles Inequalities and The Hinge Theorem
Understanding the inequalities in triangles using the Hinge Theorem. The theorem explains how the length of the third side of a triangle relates to the included angles and congruent sides in different triangle configurations. Explore problems that involve applying the Hinge Theorem and its converse
0 views • 8 slides