Understanding Triangle Classification: Sides and Angles
Explore how to classify triangles based on their sides and angles, using the Triangle Sum Theorem and linear pair theorem to find missing angle measures. Learn to distinguish between different types of triangles such as right, isosceles, equilateral, and obtuse, and solve problems involving properties of these triangles. Engage in guided practice and independent activities to reinforce learning outcomes.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
11/30: Classify a triangle by its sides and angles. Do Now: Agenda: Homework Warm-Up & Check Have Out: Handout (5 problems + 2 EC Problems) - Today s Handouts Guided Notes Guided Practice Will return graded Unit 2 tests on Friday for reflection. Independent Practice Do Now: Begin your Warm-Up Closing & HW ( maybe )
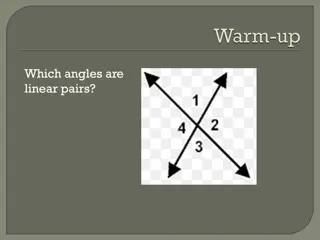
Use the linear pair theorem to find the missing triangle angle measures: Y 30 90 60 30 90 60 180 X Z
We will learn to: Classify a triangle by its sides and angles.
Graphic Organizer Use the examples and non-examples at your table to fill out your graphic organizer. Once you have finished, check with Mr. G BEFORE trying Examples 1 & 2
All 3 sides are congruent At least 2 congruent sides No sides are congruent
One obtuse angle One right angle All 3 angles are congruent All 3 angles are acute
Example 1:Classifying a Triangle by its Sides & Angles Right Triangle Isosceles Triangle Obtuse Triangle How do we know it is obtuse?
Example 2:Apply Properties of Isosceles & Equilateral Triangles 2x + 2 = 12 2x = 10 x = 5 3x 3 = 12 Check! 3(5) 3 = 12 15 3 = 12 12 = 12
Example 2:Apply Properties of Isosceles & Equilateral Triangles AB = BC 2x + 7 = 3x 2 3x 2 2x + 7 7 = x 2 9 = x 64 AB = 2x + 7 AB = 2(9) + 7 AB = 18 + 7 AB = 25 units
Example 2:Apply Properties of Isosceles & Equilateral Triangles BAC BCA 52 3x 2 2x + 7 m BCA = 64 Triangle Sum Theorem 64 64 m BAC + m BCA + m ABC = 180 m BAC ______ + ______ + ________ = 180 64 64 m ABC = 52
Example 3:Apply Triangle Sum Theorem to Classify Triangles Triangle Sum Theorem (2x + 10) m ABC + m ACB + m BAC = 180 (x + 20) (3x - 12) ______ + _______ + _______ = 180 (x + 20) (3x 12 ) (2x + 10) 6x + 18 = 180 6x = 162 x = 27
Example 3:Apply Triangle Sum Theorem to Classify Triangles m ABC = (x + 20) (2x + 10) m ABC = 47 (x + 20) (3x - 12) m ACB = (3x 12) m ACB = 69 m BAC = (2x + 10) m BAC = 64