Understanding Calculus: From MVT to FTC with Lin McMullin

Join Lin McMullin in exploring the transition from the Mean Value Theorem (MVT) to the Fundamental Theorem of Calculus (FTC). Discover the significance of MVT, Fermat's Theorem, Rolle's Theorem, and the Mean Value Theorem, all crucial concepts in calculus. Engage in graphical explorations, proving methodologies, and exam examples, culminating in a deeper understanding of these foundational principles in calculus education.

• Calculus
• Lin McMullin
• MVT
• FTC
• Graphical Explorations

batt_a Follow

Uploaded on Sep 22, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

Presentation Transcript

1. From the MVT to the FTC Presented by Lin McMullin Mass Insight Fall Conference November 2020

2. Welcome! Lin McMullin Moderator, AP Calculus Community AP Calculus AB & BC: Reviewing for the Exam AP Calculus AB & BC teacher for 30 years AP Consultant since 1991 National Director of Mathematical Programs for the National Math and Science Initiative (2008 20012) Author of Teaching AP Calculus Blogger at TeachingCalculus.com Links to resources for this session and a copy of the PowerPoint slides may be found here www.TeachingCalculus.com > Presentations > Mass Insight 2

3. From the MVT to the FTC Discovering the MVT (Group Exploration) Demonstrating (Proving) the MVT Graphical ideas (Desmos) MVT Examples from AP Exam Using the MVT to Establish the FTC 1 The FTC 2 FTC Examples from AP Exam Q & A - Anytime

4. Discovering the MVT Enter your favorite function as Y1, and graph in a convenient window 1. Store values to A and B on the home screen 2. Find slope from x = A to x = B, store as M 3. Enter equation of line thru A and B as Y2 4. Enter equation for vertical distance from function to line as Y3 5. Find extreme value(s) of Y3 6. Find the slope (derivative) of Y1 at the extreme(s) you found 7. Discuss 8.

5. Discovering the MVT

6. Fermats Theorem If a function f is continuous on a closed interval and has an extreme value (a maximum or minimum) on that interval at x = c, then the derivative at x = c is either zero or undefined. ( ) ( ) f c + f c h ( ) c = lim h f h 0 ( ) ( ) + 0 0 f c f c ( ) c = 0 or DNE f

7. Rolles Theorem If a function f is continuous on the closed interval [a, b] and ( ) f a ( ) f b = differentiable on the open interval (a, b) and if , then there is a number c in (a, b) such that ( ) = 0 f c

8. The Mean Value Theorem ? = ? ? ? ? ? ? ? ? ? ? ? ?

9. The Mean Value Theorem ( ) f b ( )( ( ) f a ( ) h x ( ) f x ( ) f a ) = x a b a ( ) h a ( ) h b ( ( ) f a ) h c = = = 0 , such that 0 c a b ( ) f b ( ) ( ) c h c = = 0 f b a ( ) f a b a ) ( ) f b = ( ) f b ( ) c = f ( )( c b a ( ) f a f

10. The Mean Value Theorem Desmos Graph Observation 1: Move the line up and down Observation 2: There may be more than one value of c Observation 3: Instantaneous Rate of Change equals Average Rate of change Observation 4: If you travel a distance at an average rate of 60 mph, then at some point your speedometer must have read 60 mph.

11. The Mean Value Theorem Darboux Jean Gaston Darboux 1842 - 1917 Darboux s Theorem: If f is differentiable on the closed interval [a, b] and r is any number between f ' (a) and f ' (b), then there exists a number c in the open interval (a, b) such that f ' (c) = r.

12. MVT Exam Questions 2003 AB 80

13. MVT Exam Questions + + 1 c (4 ln(4)) (1 ln(1)) 4 1 + = 1 2003 BC 92

14. MVT Exam Questions 2008 AB 89 / BC 89

15. MVT Exam Questions 2013 AB 22

16. MVT Exam Questions 2005 AB 5 / BC 5

17. MVT Exam Questions 2005 AB 5 / BC 5

18. MVT Exam Questions Discussion, comments, and questions on the MVT

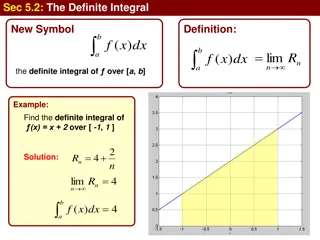
19. Riemann Sum = = a x x x x x x x b Partition of an interval [a, b] 0 1 2 1 1 i i n n * i [ , ] x x x Let 1 i i Then the Riemann sum for a function, f, on the interval is n ( ) ( k f x ) * x x 1 k k = 1 k

20. Riemann Sum The definite integral of f (x) from x = a to x = b is defined as n ( ) ( k f x b ) ( ) f x dx = * lim x x 1 k k a 0 = 1 k

21. Riemann Sum The definite integral of f (x) from x = a to x = b is defined as n ( ) ( k f x b ) ( ) f x dx = * lim x x 1 k k a 0 = 1 k The net change in f (x) on [a, b] is f (b) f (a) The net change is also the sum of the net change on each subinterval defined by the partition: ( 1 k = n ) ( ) ( ) lim n f x f x 1 k k

22. Riemann Sum n ( ) ( ) ( ) ( ) f b ( ) f a = lim n f x f x 1 k k = 1 k ( ) f b ( ) f a ( ) ( c ) = b a f The Mean Value Theorem: n ( ) ( k c ) ( ) f b ( ) f a = lim f x x 1 k k = 1 k b af ( ) x dx ( ) f b ( ) f a =

23. Fundamental Theorem of Calculus b af ( ) x dx ( ) f b ( ) f a = Use 1: The integral of a rate of change is the net amount of change. They ask for an amount, so look around for a rate to integrate!

24. Fundamental Theorem of Calculus b af ( ) x dx ( ) f b ( ) f a = Use 2: Evaluating definite integrals ( ) 5 22xdx = = 6cos x dx 2 1 2 1 2 5 22 ( ) 2 ( ) 6 ( ) x dx xdx = = = = = 2 2 5 2 21 cos sin sin 1 2 6

25. Fundamental Theorem of Calculus - 2 Examples of differentiating functions defined by an integral: x ( ) f x ( ) f x ( ) t dt = = /6cos ( ) sin ( ) 6 sin x ( ) x ( ) x = cos f

26. Fundamental Theorem of Calculus - 2 Examples of differentiating functions defined by an integral: ( ) x ( ) sin ( ) = + 3 g x t t dt 4 ( ) ( ) ( ) ( ) x ( ) x ( ) 4 2 = + 64 8 + sin sin g x 1 4 1 2 ( ( ) ( ) ( ) ( ) x ( ) x ( ) x ( ) x 3 g x = + sin cos sin cos 0 x ) ( ) ( ) x ( ) x 3 = + sin sin cos

27. Fundamental Theorem of Calculus - 2 ( ) g x x ( ) ( ) ( ) ( ) ( ) ( ) + + = = F x F a f t dt F x F a f t dt a a dF x dx dF x dx ( ) ( ) ( ) f x ( ) ( ) ( ) = = ' f g x g x

28. Integration Itineraries After teaching derivatives you can teach 1. Unit 6: Integration up to the FTC (6.1 6.7) 2. Unit 6: Antiderivatives (6.8 6.14) 3. Unit 7: Differential Equations 4. Unit 8: Integration Applications 1. Integration up to the FTC 2. Antiderivatives 3. Integration Applications 4. Differential Equations 1. Integration up to the FTC 2. Integration Applications 3. Antiderivatives 4. Differential Equations 1. Antiderivatives 2. Integration up to the FTC 3. Integration Applications 4. Differential Equations

29. FTC Exam Questions They ask for an amount, so look around for a rate to integrate! 5 ( ) E t dt = 153 0 2019 AB 1

30. FTC Exam Questions 2009 AB 3 The Mighty Cable Company

31. FTC Exam Questions They ask for an amount, so look around for a rate to integrate! 2009 AB 3 The Mighty Cable Company

32. FTC Exam Questions 30 256 ( ) = 30 (25) xdx C C 2009 AB 3 The Mighty Cable Company

33. FTC Exam Questions 2009 AB 3 The Mighty Cable Company

34. FTC Exam Questions Wire Rope Geometry

35. FTC Exam Questions 2012 AB 1 / BC 1

36. FTC Exam Questions 2012 AB 1 / BC 1

37. FTC Exam Questions 2006 AB4

38. FTC Exam Questions 2006 AB4 70 ( ) ( ) ( ) 10 = 70 v t dt h h 10

39. FTC Exam Questions 2005 AB 5 / BC 5

40. FTC Exam Questions 2005 AB 5 / BC 5

41. FTC Exam Questions 2012 BC 28

42. FTC Exam Questions Fake ( 1 ) x ( ) cos x cos t dt = 3 3 3 lim x = lim x 3 3 x 3 1 2 3 (A) 1 (B) (C) (D)1 2

43. MVT Exam Questions Discussion, comments, and questions on the FTC

44. From the MVT to the FTC Presented by Lin McMullin Mass Insight Fall Conference November 2020

45. Welcome! Lin McMullin Moderator, AP Calculus Community AP Calculus AB & BC: Reviewing for the Exam AP Calculus AB & BC teacher for 30 years AP Consultant since 1991 National Director of Mathematical Programs for the National Math and Science Initiative (2008 20012) Author of Teaching AP Calculus Blogger at TeachingCalculus.com Links to resources for this session and a copy of the PowerPoint slides may be found here www.TeachingCalculus.com > Presentations > Mass Insight 45