Exploring Spiritual Quotient (SQ) and Its Significance in Personal Growth
Spiritual Quotient (SQ) measures an individual's spiritual intelligence and capacity for understanding spiritual concepts. It encompasses attributes like wisdom, transcendence, and humility, emphasizing the spiritual dimension of human experience. SQ, associated with spiritual intelligence, can lead
0 views • 7 slides
Womens Trousers A Guide to Finding the Perfect Fit
Style quotient trousers for women. Trousers and bottomwear for everyday casual formal and office wear. stylish and fashionable. affordable fashion. Indian fashion brand style quotient. New and trendy styles. Fast fashion. make in India.
2 views • 11 slides
Understanding Conditional Probability and Bayes Theorem
Conditional probability relates the likelihood of an event to the occurrence of another event. Theorems such as the Multiplication Theorem and Bayes Theorem provide a framework to calculate probabilities based on prior information. Conditional probability is used to analyze scenarios like the relati
1 views • 5 slides
Understanding Boolean Algebra: Duality Theorem, De-Morgan's Law, and Don't Care Conditions
Boolean algebra concepts such as the Duality Theorem, De-Morgan's Law, and Don't Care Conditions are essential for digital circuit design. The Duality Theorem states the relationship between a Boolean function and its dual function by interchanging AND with OR operators. De-Morgan's Law helps find t
0 views • 10 slides
Understanding the Coase Theorem: Property Rights and Economic Efficiency
The Coase Theorem, developed by economist Ronald Coase, posits that under certain conditions, bargaining related to property rights will lead to an optimal outcome regardless of the initial distribution. It provides a framework for resolving conflicts by emphasizing negotiation and efficient market
0 views • 10 slides
Understanding the Fundamental Theorem of Calculus
The Fundamental Theorem of Calculus states that if a function is continuous on an interval and has an antiderivative on that interval, then the integral of the function over the interval is equal to the difference of the antiderivative evaluated at the endpoints. This concept is further explored thr
0 views • 14 slides
Understanding Myhill-Nerode Theorem in Automata Theory
Myhill-Nerode theorem states that three statements are equivalent regarding the properties of a regular language: 1) L is the union of some equivalence classes of a right-invariant equivalence relation of finite index, 2) Equivalence relation RL is defined in a specific way, and 3) RL has finite ind
1 views • 20 slides
Understanding the Pythagorean Theorem and Right-Angled Triangles
Explore the Pythagorean Theorem, which states that in a right-angled triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the other two sides (a and b). Learn how to identify the hypotenuse, use the theorem to find missing lengths, and visually understand th
0 views • 25 slides
Engineering Mechanics: Lami's Theorem and Cylinder Reactions Problem
This course material covers Lami's Theorem in Engineering Mechanics taught by Ranbir Mukhya. It includes an outline of the theorem, problem scenarios involving cylinders with given weights and diameters, and the determination of reactions at various points. Detailed force diagrams and calculations a
0 views • 8 slides
Insights into the Mean Value Theorem and Its Applications
Delve into the Mean Value Theorem (MVT) with a focus on concepts like Lagrange's MVT, Rolle's Theorem, and the physical and geometrical interpretations. Explore the conditions, statements, and special cases of MVT, along with practical applications and geometric insights. Dr. Arnab Gupta, an Assista
0 views • 14 slides
Understanding Exterior Angles in Polygons
This content explains the concept of exterior angles in polygons and the Exterior Angle Theorem. It covers how exterior angles are formed when the sides of a polygon are extended, their relationship with interior angles, and how to calculate their measures using the Exterior Angle Theorem. Various e
2 views • 26 slides
Understanding the Residue Theorem in Complex Analysis
The Residue Theorem is a powerful tool in complex analysis that allows us to evaluate line integrals around paths enclosing isolated singularities. By expanding the function in a Laurent series, deforming the contour, and summing residues, we can evaluate these integrals efficiently. This theorem ex
0 views • 31 slides
Understanding Superposition Theorem in Electrical Circuits
Superposition theorem in electrical circuits states that the effects of multiple voltage and current sources in a network can be analyzed independently and then combined algebraically. This allows for calculating the voltage and current distribution in a network more efficiently. The theorem involve
0 views • 9 slides
Understanding Spiritual Quotient (SQ) and Its Significance
Spiritual Quotient (SQ) measures a person's spiritual intelligence and capacity for spiritual growth. It encompasses qualities such as wisdom, transcendence, and humility, focusing on the spiritual dimension of human experience. SQ involves self-awareness, empathy, and the pursuit of higher truths,
0 views • 7 slides
Understanding Lami's Theorem in Physics
Lami's Theorem is an equation that explains how the magnitudes of forces acting on a point keep an object in equilibrium. This theorem relates the forces with corresponding angles and is derived by understanding the sum of forces acting on a point. By utilizing complementary angles and the sine rule
0 views • 8 slides
Understanding the Central Limit Theorem in Statistics
This lesson covers the Central Limit Theorem, which states that the sampling distribution of a sample mean becomes approximately normal as the sample size increases, regardless of the population distribution. It explains how the distribution of sample means changes shape and approaches a normal dist
0 views • 7 slides
Understanding Quotient Spaces in Mathematics
In group theory, a subgroup H of a group G helps decompose G into equal-size disjoint subsets called cosets. Quotient spaces in mathematics involve equivalence classes under a given relation and a specific topology. Furthermore, in linear algebra, the quotient of a vector space by a subspace results
0 views • 8 slides
Exploring the Pythagorean Theorem and Its Origins
The Pythagorean Theorem, named after the ancient Greek mathematician Pythagoras, is a fundamental principle in geometry relating to right triangles. While Pythagoras is credited with offering a proof of the theorem, evidence suggests that earlier civilizations like the Babylonians and ancient Chines
0 views • 21 slides
Understanding the Pythagorean Theorem: History, Application, and Baseball Problem
Pythagoras, a renowned mathematician from ancient times, formulated the Pythagorean Theorem to calculate the lengths of sides in right triangles. This theorem has significant implications in various fields, aiding in distance computation, navigation, and ramp design. Moreover, its practical applicat
0 views • 14 slides
Understanding Rolle's Mean Value Theorem in Calculus
Rolle's Mean Value Theorem states that if a function is continuous in a closed interval, differentiable in the open interval, and the function values at the endpoints of the interval are equal, then there exists at least one point where the derivative of the function is zero. This theorem is verifie
0 views • 11 slides
Understanding Bayes Theorem in NLP: Examples and Applications
Introduction to Bayes Theorem in Natural Language Processing (NLP) with detailed examples and applications. Explains how Bayes Theorem is used to calculate probabilities in diagnostic tests and to analyze various scenarios such as disease prediction and feature identification. Covers the concept of
0 views • 13 slides
Understanding Division and Floating Point Arithmetic
Explore the concepts of division and IEEE 754 representations in floating point arithmetic. Learn about the processes involved in division, including steps to find quotient and remainder. Delve into an example of dividing numbers along with hardware implementation for efficient division.
0 views • 19 slides
Understanding Greatest Common Divisor and Euclidean Algorithm
Learn about the concept of greatest common divisors (GCD), how to compute them efficiently using the Euclidean Algorithm, the Quotient-Remainder Theorem, and the properties of common divisors. Explore examples and applications of GCD, extending to linear combinations, prime factorization, and other
0 views • 45 slides
Basics of Division in Number Theory and Encryption
Understanding arithmetic operations for discrete numbers is crucial in the world of Number Theory and Encryption. This session covers the fundamentals of addition, subtraction, multiplication, and division, emphasizing key terms like dividend, numerator, divisor, quotient, remainder, and fraction. T
0 views • 7 slides
Understanding Division of Polynomials using Remainder and Factor Theorem
Explore the concept of dividing polynomials to find remainders and factors, illustrated through examples and explanations. Learn how to apply the Remainder and Factor Theorem to determine remainders, factors, and solve related problems. Test your understanding with practical questions.
0 views • 17 slides
Polynomial Division Methods and Examples
Dividing polynomials involves using methods like long division or equating coefficients. By applying these techniques, you can determine whether a polynomial divides exactly or leaves a remainder. The process is similar to long division of numbers, where the dividend is divided by the divisor to obt
0 views • 10 slides
Understanding Remainders in Division Problems
Interpreting remainders in division involves various ways based on the situation and question. Sometimes, you focus on the quotient, while in other cases, you include the remainder in different ways such as adding 1 to the quotient or presenting it as a fraction. This concept is illustrated through
0 views • 11 slides
Polynomial Division and Remainder Theorems Explained
Learn how to use long division to find quotients and remainders in polynomial problems. Understand when to use long division or synthetic division. Discover how the remainder theorem works by finding remainders when dividing specific polynomials by different factors. Explore the factor theorem and i
0 views • 6 slides
Polynomial and Synthetic Division Techniques
Learn how to perform polynomial division using long division and synthetic division methods. Understand how to divide polynomials by other polynomials or binomials, utilize the Remainder Theorem and Factor Theorem, and apply these concepts through detailed examples.
0 views • 41 slides
Problem Solving with Pythagoras Theorem in Geometry
Explore the application of Pythagoras Theorem in solving problems related to right-angled triangles, diagonals of shapes like rectangles and rhombuses, and the height of triangles. Learn how to use Pythagoras Theorem effectively by drawing diagrams, identifying known lengths, and using the theorem t
0 views • 8 slides
Understanding Integer Division, Modulus, and Parity
Explore the concepts of integer division, modulus, and the parity of integers through the quotient-remainder theorem. Learn how to compute div and mod manually and understand the representation of integers as even or odd. Discover how these principles apply in computer languages and the unique prope
0 views • 18 slides
Exploring Bloom and Quotient Filters in CSCI 333
Delve into the world of Bloom and Quotient filters in CSCI 333, understanding their operations, growth methods, and handling when exceeding RAM limits. Discover how Bloom filters support certain operations, learn about Quotient filters based on techniques from Donald Knuth's work, and explore buildi
0 views • 10 slides
Understanding Calculus: From MVT to FTC with Lin McMullin
Join Lin McMullin in exploring the transition from the Mean Value Theorem (MVT) to the Fundamental Theorem of Calculus (FTC). Discover the significance of MVT, Fermat's Theorem, Rolle's Theorem, and the Mean Value Theorem, all crucial concepts in calculus. Engage in graphical explorations, proving m
0 views • 45 slides
Understanding Rolle's Theorem and The Mean Value Theorem in Calculus
Rolle's Theorem states that for a continuous and differentiable function on a closed interval with equal function values at the endpoints, there exists at least one point where the derivative is zero. The Mean Value Theorem asserts that for a continuous and differentiable function on an interval, th
0 views • 5 slides
Introduction to Analysis: Mean Value Theorem and Related Theorems
This resource delves into key concepts such as the Mean Value Theorem, Fermat's Theorem, Rolle's Theorem, Extreme Value Theorem, local maximums, and more. It presents important results and explores proofs in the context of analysis.
0 views • 71 slides
Introduction to Applying Pythagorean Theorem in Right Triangles
In this lesson, we will learn how to apply the Pythagorean Theorem to find missing side lengths of right triangles. The Pythagorean Theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Through examples and practice problems,
0 views • 13 slides
Understanding Binomial Theorem: Expansion, Examples, and Applications
Binomial theorem is a powerful mathematical concept used to expand expressions involving binomials. This presentation explores the basics of binomial expansion, formulae for positive, negative, and fractional indices, along with examples demonstrating its application. By leveraging the binomial theo
0 views • 10 slides
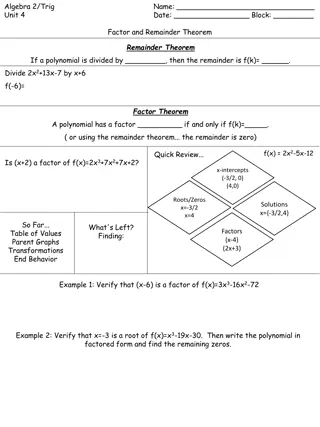
Understanding Polynomial Factor and Remainder Theorems
Exploring the Factor and Remainder Theorems in algebra, including examples on verifying factors, finding roots, applying the Rational Root Test, and determining zeros of polynomials. Learn how to factor polynomials, find remaining zeros, and analyze coefficients to uncover the complete factorization
0 views • 6 slides
Understanding Automated Theorem Proving in Lean
Dive into the world of automated theorem proving in Lean with a focus on formal verification, history, and the use of logic and computational methods. Explore how programs can assist in finding and verifying proofs, as well as the significance of interactive theorem provers. Discover the evolution o
0 views • 35 slides
Triangles Inequalities and The Hinge Theorem
Understanding the inequalities in triangles using the Hinge Theorem. The theorem explains how the length of the third side of a triangle relates to the included angles and congruent sides in different triangle configurations. Explore problems that involve applying the Hinge Theorem and its converse
0 views • 8 slides