Understanding Remainders in Division Problems
Interpreting remainders in division involves various ways based on the situation and question. Sometimes, you focus on the quotient, while in other cases, you include the remainder in different ways such as adding 1 to the quotient or presenting it as a fraction. This concept is illustrated through examples involving a school relay race, showcasing how to interpret remainders effectively.
Uploaded on Sep 14, 2024 | 0 Views
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Making Sense of Remainders INTERPRETING THE REMAINDER MAFS.4.OA.1.A
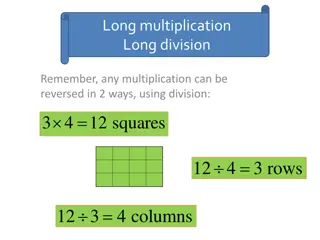
Interpreting the Remainder When you solve a division problem with a remainder, the way you interpret the remainder depends on the situation and the question. Ways to Interpret the Remainder Sometimes you only use the quotient. Another way is to add 1 to the quotient. Situations when it is necessary to include all items. Other times you will only use the remainder. One way is to write the remainder as a fraction. This often applies when solving problems using measurement units, like distances, length and time. Write the remainder as the numerator and the divisor is the denominator. Remember to simplify all fractions and use the whole number in your final answer.
The annual school relay is on Saturday. This year 75 students from 4thgrade plan to run the race. Each relay team can have up to 8 runners. How many teams will fourth grade have this year?
Quotient + 1 Explanation: The numerical answer to the question is 9 r 3. However, to ensure that all runners have an opportunity to participate in the relay, there must be 10 teams. There will be 9 teams with 8 runners and 1 team with 3 runners, making a total of 10 teams.
The annual school relay is on Saturday. This year 75 students from 4thgrade plan to run the race. Each relay team can have up to 8 runners. How many runners will make up the last team? How many runners are not on a team of 8?
Using Only the Remainder Explanation: The numerical answer to the question is 9 r 3. However, the answer to this question is simply 3. The remainder 3, reflects the remaining number of runners, who were unable to make a complete group of 8.
The annual school relay is on Saturday. This year 75 students from 4thgrade plan to run the race. Each relay team can have up to 8 runners. How many teams of 8 will fourth grade have this year?
Using Only the Quotient Explanation: The numerical answer to the question is 9 r 3. However, the answer the question is 9 teams. In this case, the remainder is not needed in answering the question, because the remainder reflects the number of runners that do not make up a team of 8.
The length of the annual relay 75 meters. You have 8 days to prepare for the relay. If you plan to run the same exact amount each day, how far will you run each day?
Remainder as a Fraction Explanation: The numerical answer to the question is 9 r 3. However, for this question, the remainder must be interpreted as a fraction to make sure you account for the total distance/dividend in this problem. To express the remainder as a fraction, the remainder is your numerator and your denominator is the divisor. The answer therefore will be, 9 and 3/8 meters each day.
Interpreting the Remainder When you solve a division problem with a remainder, the way you interpret the remainder depends on the situation and the question. Ways to Interpret the Remainder Sometimes you only use the quotient. Another way is to add 1 to the quotient. Situations when it is necessary to include all items. Other times you will only use the remainder. One way is to write the remainder as a fraction. This often applies when solving problems using measurement units, like distances, length and time. Write the remainder as the numerator and the divisor is the denominator. Remember to simplify all fractions and use the whole number in your final answer.