Language Teaching Techniques: GTM, Direct Method & Audio-Lingual Method
Explore the Grammar-Translation Method, Direct Method, and Audio-Lingual Method in language teaching. Understand principles, objectives, and methodologies with insights into language learning approaches. Enhance teaching skills and foster effective communication in language education.
7 views • 82 slides
And Applying Numerical Analysis in Statistics
Utilize numerical analysis techniques to interpret and manipulate numerical data effectively in various environments. Enhance your understanding of value placement in digital contexts to make informed decisions based on positioning and order. Develop skills in reading, writing, and interpreting numb
7 views • 36 slides
Data Types and Summary Statistics in Exploratory Data Analysis
Data types, including discrete numerical, continuous numerical, ordinal, and nominal, are essential in exploratory data analysis. Variables can be categorized based on their nature, such as numerical variables (interval vs. ratio) and categorical data summaries. Learn about USGS flow measurements, n
4 views • 48 slides
Ensuring Reliability of Deep Neural Network Architectures
This study focuses on assuring the reliability of deep neural network architectures against numerical defects, highlighting the importance of addressing issues that lead to unreliable outputs such as NaN or inf. The research emphasizes the widespread and disastrous consequences of numerical defects
0 views • 26 slides
Different Emasculation Techniques in Plant Breeding
Learn about the significance of emasculation in plant breeding to prevent self-pollination and facilitate controlled pollination. Explore various methods such as hand emasculation, forced open method, clipping method, emasculation with hot/cold water, alcohol, suction method, chemical emasculation,
3 views • 10 slides
Numerical Problems on Floatation and Metacentric Heights in Marine Engineering
Solve numerical problems related to floatation and metacentric heights in marine engineering, including calculations for metacentric height, centre of gravity, displacement, and angles of tilt. Examples involve ships, pontoons, and calculating dimensions such as breadth and height for floating struc
2 views • 5 slides
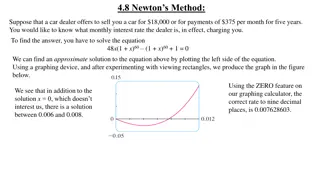
Newton's Method for Solving Equations
Newton's Method, also known as the Newton-Raphson method, is a powerful tool for approximating roots of equations. By iteratively improving initial guesses using tangent lines, this method converges towards accurate solutions. This method plays a crucial role in modern calculators and computers for
0 views • 12 slides
The Conjugate Beam Method in Structural Analysis
The Conjugate Beam Method is a powerful technique in structural engineering, derived from moment-area theorems and statical procedures. By applying an equivalent load magnitude to the beam, the method allows for the analysis of deflections and rotations in a more straightforward manner. This article
1 views • 11 slides
Roots of Equations in Engineering: Methods and Techniques
Roots of equations are values of x where f(x) = 0. This chapter explores various techniques to find roots, such as graphical methods, bisection method, false position method, fixed-point iteration, Newton-Raphson method, and secant method. Graphical techniques provide rough estimates, while numerica
0 views • 13 slides
Numerical Methods and Errors in Computation
Delve into the world of numerical methods through the guidance of Dr. M. Mohamed Surputheen. Explore topics such as solving algebraic and transcendental equations, simultaneous linear algebraic equations, interpolation, numerical integration, and solving ordinary differential equations. Learn about
0 views • 130 slides
Mathematical Modeling and Error Analysis in Engineering
Mathematical modeling plays a crucial role in solving engineering problems efficiently. Numerical methods are powerful tools essential for problem-solving and learning. This chapter explores the importance of studying numerical methods, the concept of mathematical modeling, and the evaluation proces
0 views • 10 slides
Interpolation in Numerical Methods
Interpolation is a fundamental mathematical operation used in numerical methods to find the value of a function between known data points. It involves computing the value of a function at any point within a given interval based on existing data. Newton's forward interpolation formula is commonly use
0 views • 18 slides
Determination of Dipole Moment in Chemistry
The determination of dipole moment in chemistry involves methods such as the Temperature Method (Vapour Density Method) and Refractivity Method. These methods rely on measuring various parameters like dielectric constants and polarizations at different temperatures to calculate the dipole moment of
1 views • 15 slides
Comprehensive Overview of Numerical Linear Algebra Methods for Solving Linear Systems
Explore numerical linear algebra techniques for solving linear systems of equations, including direct and iterative methods. Delve into topics like Gaussian elimination, LU factorization, band solvers, sparse solvers, iterative techniques, and more. Gain insights into basic iterative methods, error
6 views • 12 slides
Introduction to Numerical Methods: A Comprehensive Overview
Numerical methods play a crucial role in solving mathematical problems efficiently through arithmetic operations. This lecture by Dr. Nur Uddin covers the fundamental concepts of numerical methods, emphasizing their importance in engineering problem-solving with the use of modern digital computers.
1 views • 17 slides
Introduction to Numpy and Scipy: Numerical Computing in Python
Numpy and Scipy provide powerful MATLAB-like functionality in Python for fast numerical computations, high-level math functions, and efficient handling of multidimensional arrays. Learn why NumPy is essential for speeding up numerical computations in Python and explore key features such as arrays, m
0 views • 47 slides
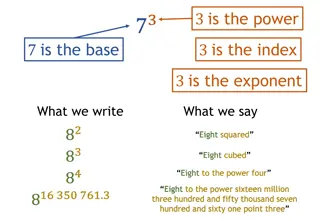
Numerical Expressions and Exponents Overview
This content covers various numerical expressions involving exponents, including examples of valid and invalid mathematical representations, matching worded expressions with their numerical equivalents, and identifying the correct expressions based on provided criteria.
0 views • 30 slides
Numerical Abstract Domain with Max Operator in Timing Analysis
Explore a numerical abstract domain based on expression abstraction and the Max operator with applications in timing analysis. The challenges in timing analysis, such as disjunctive and non-linear bounds, are discussed along with simple examples illustrating these concepts. The difficulty of proving
0 views • 21 slides
Overview of Sparse Linear Solvers and Gaussian Elimination
Exploring Sparse Linear Solvers and Gaussian Elimination methods in solving systems of linear equations, emphasizing strategies, numerical stability considerations, and the unique approach of Sparse Gaussian Elimination. Topics include iterative and direct methods, factorization, matrix-vector multi
0 views • 35 slides
Measurement of Flow Velocity on Frozen and Non-Frozen Slopes of Black Soil Using Leading Edge Method
This study presented a detailed methodology for measuring flow velocity on frozen and non-frozen slopes of black soil, focusing on the Leading Edge method. The significance of shallow water flow velocity in soil erosion processes was emphasized. Various methods for measuring flow velocity were compa
0 views • 23 slides
Introduction to Python for Numerical Computing and Scientific Application
This document introduces the use of Python for numerical computing and development of scientific applications in the context of Civil and Environmental Engineering. It covers topics such as utilizing the SciPy ecosystem, creating graphs using pylab/matplotlib, plotting 3D graphs, and working with Pa
0 views • 36 slides
Chemical Kinetics and Numerical Solvers in Chemistry
Explore the principles of chemical kinetics and the use of numerical solvers to compute concentrations over time, considering explicit and implicit methods. Understand stability and positivity requirements in solvers and the importance of characteristic time scales in chemical systems. Dive into a s
0 views • 5 slides
Best Practices for Including Code and Numerical Results in Statistics-related Dissertations
Include important code snippets in an appendix, describe work in detail in the main body, mention coding in introduction, present numerical results appropriately, format figures optimally for statistics-related dissertations.
0 views • 5 slides
Study of Fluid Dynamics around Moth Centerboard using OpenFOAM: Advanced Course
Dive into the advanced fluid dynamics course focusing on the foiling moth centerboard simulated on OpenFOAM. Explore the features of a moth, set targets for the study, choose the numerical solver, define boundary conditions, create geometry, meshing, and analyze results through numerical simulations
0 views • 17 slides
Sketching Techniques for Efficient Numerical Linear Algebra on Massive Data Sets
Explore how sketching methods can be applied in numerical linear algebra to handle massive data sets efficiently. David Woodruff of IBM Almaden discusses using randomized approximations for algorithms aiming for nearly linear time complexity. Applications include analyzing internet traffic logs, fin
0 views • 95 slides
Numerical Chromosome Aberrations in Humans
Numerical chromosome aberrations involve the gain or loss of whole chromosomes, impacting the genome size and potentially leading to genetic mutations. Nondisjunction, where chromosomes fail to separate properly during cell division, can result in aneuploidy - the presence of an extra or missing chr
0 views • 18 slides
Mathematics Bridging Course Highlights from Tseung Kwan O Catholic Primary School
In the Mathematics Bridging Course for the Secondary Curriculum at Tseung Kwan O Catholic Primary School, students are introduced to important terms related to directed numbers, such as positive and negative numbers, absolute value, and numerical comparisons. The course covers fundamental concepts l
0 views • 17 slides
Python for Numerical Computing and Development of Scientific Applications - Class Concepts and Inheritance
In this lesson, we delve into class concepts and inheritance in Python for numerical computing and developing scientific applications. Learn about defining classes, creating instances, inheritance, special methods, private attributes/methods, and more. Explore practical examples and code snippets to
0 views • 27 slides
Numerical Solution of Eulerian Advection Equation in 1-D Operator Splitting
Application of operator splitting over three directions allows reducing the Eulerian advection equation to 1-D, enabling finite differencing of derivatives while maintaining conservation properties. Various numerical schemes like forward Euler, leapfrog, and linear upstream are discussed, highlighti
0 views • 8 slides
Numerical Methods for Root Finding and Iteration
Explore the concepts of root finding, locating roots, stationary points, and iteration in numerical methods. Learn to determine roots, stationary points, and convergence/divergence types, as well as apply the Newton-Raphson method for function approximation.
0 views • 17 slides
Numerical Methods in Mathematics
Explore the world of numerical methods in mathematics, focusing on the Newton-Raphson Method and root approximations. Discover how to locate roots of equations and use iteration to enhance your problem-solving skills. Uncover the significance of numerical methods in finding solutions to complex equa
0 views • 28 slides
An Overview of Finite Element Method in Mechanical Engineering
Finite Element Method (FEM) in mechanical engineering is a powerful numerical technique involving dividing a domain into finite elements, establishing relations between variables, and assembling elements to analyze a system. This method is fundamental for solving one-dimensional problems and approxi
0 views • 63 slides
Shoe Lace Method for Finding Polygon Areas
The Shoe Lace Method is a mathematical process used to determine the area of any polygon by employing coordinate geometry. By following specific steps, including organizing coordinates, multiplying diagonally, and adding columns in a certain manner, the method allows for a straightforward calculatio
0 views • 8 slides
Unsteady MHD Poiseuille Flow Through a Porous Channel
This study investigates unsteady magnetohydrodynamic (MHD) Poiseuille flow through a porous channel under an oscillating pressure gradient and uniform suction/injection. The objective is to obtain numerical solutions for the velocity distribution and analyze how the velocity is affected by various p
0 views • 16 slides
Overview of Numerical Methods in Computational Fluid Dynamics
This material delves into the properties, discretization methods, application in PDEs, grid considerations, linear equations solution, and more involved in Numerical Methods in Computational Fluid Dynamics. It covers approaches to fluid dynamical problems, components of numerical methods, and their
0 views • 40 slides
Numerical Study of Submerged Oil Leak Jet
This study focuses on a numerical investigation of a submerged turbulent oil jet, aiming to calculate the oil discharge rate despite the opaque nature of the oil. The research involves experimental test cases, CFD simulations, and analysis of large and small-scale structures in the oil-water interfa
0 views • 24 slides
Numerical Analysis of Aerodynamic Performances in Biplane Configuration
This paper presents a numerical investigation comparing single versus double wing (biplane) configurations for aerodynamic performances. Geometric models and numerical analyses were conducted, providing insights into the advantages and complexities of biplane wings. The study utilized computational
0 views • 12 slides
Quantitative Data Analysis in Research
Dive into the world of quantitative data analysis with a focus on frequencies, central tendency, dispersion, and standard deviation. Explore the collection and analysis of numerical data, levels of measurement, and methods for quantifying social concepts. Learn about the importance of capturing data
0 views • 25 slides
Math Expressions Exploration for Elementary Students
This content discusses numerical and algebraic expressions, teaching students how to match written expressions to numerical expressions, understand the concept of variables, and differentiate between algebraic and numerical expressions. It also covers basic operations like addition, subtraction, mul
0 views • 11 slides
Golden Section Search Method - Theory
The Golden Section Search Method is a numerical optimization technique used to efficiently find the optimal value within a specified interval. This method divides the search space using the golden ratio to narrow down the optimal solution with minimal iterations. By selecting intermediate points str
0 views • 18 slides