Numerical Solution of Eulerian Advection Equation in 1-D Operator Splitting
Application of operator splitting over three directions allows reducing the Eulerian advection equation to 1-D, enabling finite differencing of derivatives while maintaining conservation properties. Various numerical schemes like forward Euler, leapfrog, and linear upstream are discussed, highlighting diffusive and dispersive behaviors. Additionally, finite-volume upstream schemes ensure mass conservation by solving for momentum and scalars on staggered grids.
- Numerical solution
- Eulerian advection
- Operator splitting
- Finite differencing
- Conservation properties
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
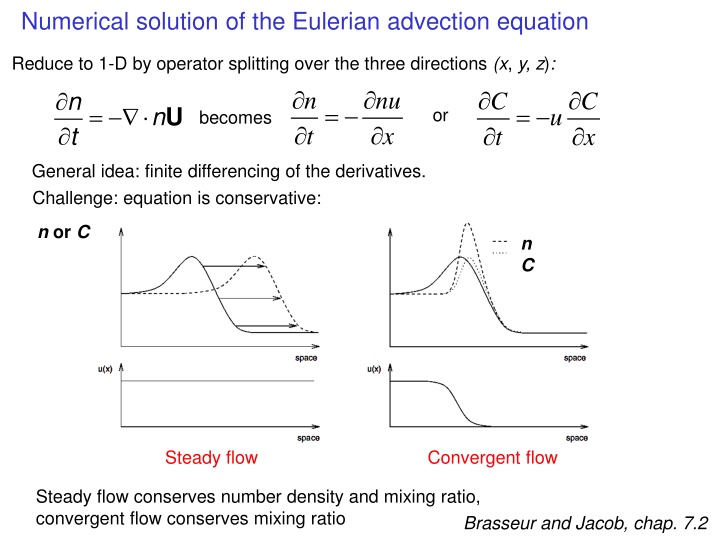
Numerical solution of the Eulerian advection equation Reduce to 1-D by operator splitting over the three directions (x, y, z): = n t nu x n t C t C x = = n U becomes u or General idea: finite differencing of the derivatives. Challenge: equation is conservative: n or C n C Steady flow Convergent flow Steady flow conserves number density and mixing ratio, convergent flow conserves mixing ratio Brasseur and Jacob, chap. 7.2
Finite-difference approximation of derivative d/dx Obtained by truncation of Taylor series; truncated term defines the order of approximation j value for gridpoint j j-1 j j+1 x xj-1 xj x xj+1 Taylor series: i i ( ) x d dx = + + 1 j j i ! i = 1 i j (x) d /dx . xj 1 xj xj+1 Brasseur and Jacob, chap. 4.8.1
First-order forward: d dx d dx ( ) ( ) 2 2 + 1 j j = + + = + ( ) ( ) x O x O x Taylor series: + 1 j j x j j Second-order central: ( ) 2 x 2 d dx d dx ( ) 3 = + + + ( ) x O x Taylor series (forward): + 1 j j 2 2 j j ( ) 2 x 2 d dx d dx ( ) 3 = + + ( ) x O x Taylor series (backward): 1 j j 2 2 j j d dx ( ) 3 = + 2 ( ) x O x Take difference: + 1 1 j j j d dx ( ) 3 + 1 2 1 j j = + ( ) O x x j
Numerical advection schemes can be diffusive and/or dispersive Advection of square wave in steady flow for 40 steps with Courant number = u t/ x = 0.5 C Forward Euler Forward Euler scheme: forward 1st-order derivative in time, central 1st-order derivative in space Numerically unstable C t=40 Leapfrog Leapfrog scheme: central 1st-order derivatives in time and space Highly dispersive, negative values t=0 Exact C Linear upstream scheme: forward 1st-order derivative in time, 1st-order upstream derivative in space Upstream Highly diffusive Brasseur and Jacob, chap. 7.3.4
Finite-volume upstream schemes gridbox (un)j-1/2 (un)j+1/2 j-1 j j+1 t n n + j t , t j t , = ( un ) ( un ) + j 1/2, t j 1/2, t Mass conservation is ensured; Interpolation error at gridbox edges is reduced by solving for momentum and scalars on staggered grids nj is now the mean number density in gridbox j Still need to relate nj1/2 to nj-1, nj+1/2to nj nj uj+1/2 uj-1/2 Scalars are solved at gridbox centers (A-grid) Momentum is solved at gridbox faces (C-grid) Brasseur and Jacob, chap. 7.4
Numerical diffusion in a finite-volume upstream scheme Assume nj+1/2 = nj; concentration at upstream boundary = mean of upstream box 1 n = u t/ x is the Courant number = 0.5 to j j+1 j+2 j+3 n = 0.5 0.5 0.5 to + t j j+1 j+2 j+3 1 true solution n 0.5 to + 2 t 0.25 0.25 j j+1 j+2 j+3 Brasseur and Jacob, chap. 7.4
Slopes scheme to reduce numerical diffusion n 1 within gridbox: nj(x) = nj + ax mean slope = 0.5 to j j+1 j+2 j+3 n 1 = 0.5 to + t j j+1 j+2 j+3 1 true solution n 0.75 to + 2 t 0.125 0.125 j j+1 j+2 j+3 Piecewise parabolic method (PPM) in GEOS-Chem uses 2nd-order polynomials Brasseur and Jacob, chap. 4.8
Semi-Lagrangian advection Determine concentration at gridpoint (or grid vertex) A at time tn+1 = tn+ t by advecting a Lagrangian air parcel back in time over t and inferring the concentration at the departure point D by interpolation on the model grid Model grid Allows transport time steps larger than the Courant limit Single transport calculation for all species But does not conserve mass (posterior correction needed) Brasseur and Jacob, chap. 7.8
