Numerical Expressions and Exponents Overview
This content covers various numerical expressions involving exponents, including examples of valid and invalid mathematical representations, matching worded expressions with their numerical equivalents, and identifying the correct expressions based on provided criteria.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
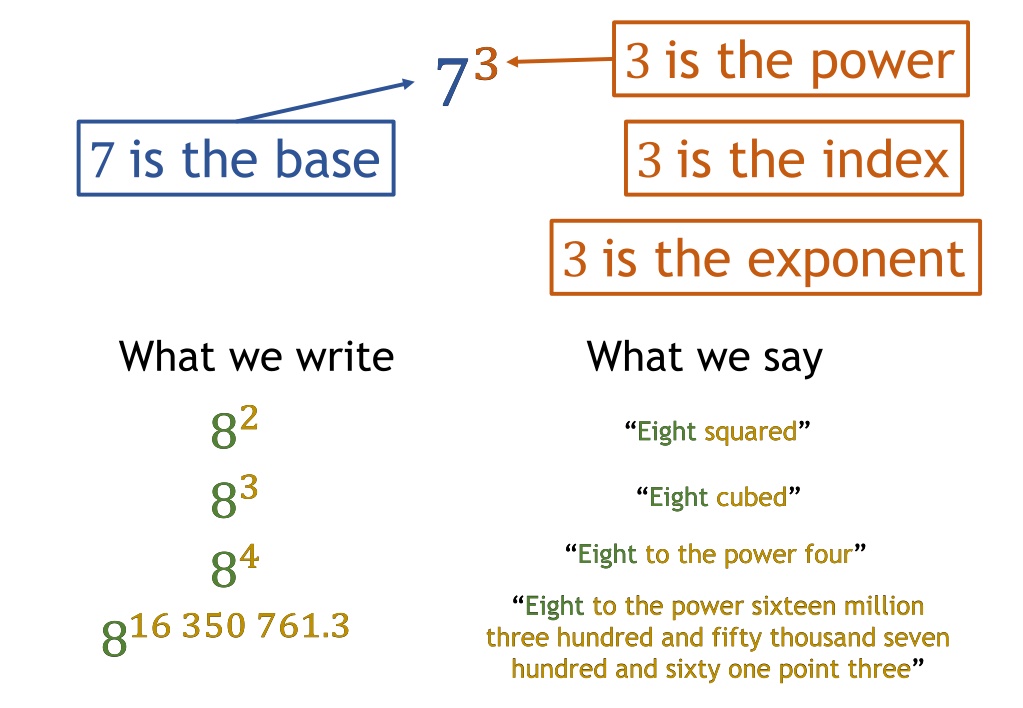
3 is the power 73 73 7 is the base 3 is the index 3 is the exponent What we write What we say 82 82 83 83 84 84 Eight squared Eight squared Eight cubed Eight cubed Eight to the power four Eight to the power four Eight to the power sixteen million three hundred and fifty thousand seven hundred and sixty one point three hundred and sixty one point three Eight to the power sixteen million three hundred and fifty thousand seven 816 350 761.3 816 350 761.3
Sort each expression below into the correct box on the left. Represents three to the power of two 2 32 3 + 3 3 Mathematically valid but doesn t represent three to the power of two 2 3 3 3 3 2 3 3 2 2 3 2 Currently mathematically meaningless 2 3 2 + 2 + 2 32 2 2 2
Sort each expression below into the correct box on the left. Represents three to the power of two 2 3 3 3 Mathematically valid but doesn t represent three to the power of two 3 2 3 + 3 2 2 2 2 + 2 + 2 Currently mathematically meaningless 3 2 2 2 3 32 3 2 3 32 2 3
57 63 102 919 36 75
Match each worded expression with its numerical equivalent 92 29 One squared One cubed Two to the power one 1221 Two cubed Nine to the power two 4994 Three to the power one Three squared 4224 Four to the power nine Four squared 32 23 Nine to the power four Two to the power four Two to the power nine 13 31
Match each worded expression with its numerical equivalent 12 13 One cubed One squared 23 21 Two to the power one Two cubed 31 92 Three to the power one Nine to the power two 49 32 Four to the power nine Three squared Four squared 42 94 Nine to the power four Two to the power four 29 24 Two to the power nine
For 1-7, write down the expression in digits, for 8-13 write down the expression in words. 57 1) Seven to the power six 8) 2) Six to the power seven 63 9) 3) Eighteen squared 102 4) Fourteen thousand cubed 10) 5) Nineteen million three hundred thousand 919 11) and five to the power two 36 6) Zero point seven three to the power nine 12) 7) Sixteen point zero one to the power eight 75 13) million and six thousand
For 1-7, write down the expression in digits, for 8-13 write down the expression in words. 57 76 1) Seven to the power six 8) Five to the power seven 67 2) Six to the power seven 63 9) 182 3) Eighteen squared Six cubed or six to the power three 140003 102 4) Fourteen thousand cubed 10) Ten square or ten to the power two 5) Nineteen million three hundred thousand 919 11) 193000052 and five to the power two Nine to the power nineteen 0.739 36 6) Zero point seven three to the power nine 12) Three to the power six 7) Sixteen point zero one to the power eight 75 13) 16.01800600 million and six thousand Seven to the power five
33+ 3 = 30 122+ 112= 265 23+ 2 = 10 33 32= 2187 13+ 63+ 10 = 227 72 43= 3136 23+ 33= 35 102 102 102= 1 000 000 53 23= 118 63 3 = 72 122 3 = 48 72 23= 41 63 102= 2.16 43 42= 48 72 33 102 82 43= 0 = 13.23 102+ 53= 225
33+ 3 = 30 122+ 112= 265 23+ 2 = 10 33 32= 2187 13+ 63+ 10 = 227 72 43= 3136 23+ 33= 35 102 102 102= 1 000 000 53 23= 118 63 3 = 72 122 3 = 48 72 23= 41 63 102= 2.16 43 42= 48 72 33 102 82 43= 0 = 13.23 102+ 53= 225
Write each power in expanded form and using commutativity to show that they are square numbers in disguise. Shy Squares 34 92 3 3 3 3 (3 3) (3 3) 106 10002 22 32 22 54 2 2 5 5 5 5 73 7 5 72 5 6 24 6 5 (2 5) 2 5 10 2 6 23 3 (3 2) 2 2 2 3 152 25 8 5 4 40
Write each power in expanded form and using commutativity to show that they are square numbers in disguise. Shy Squares 34 92 3 3 3 3 (3 3) (3 3) 106 10002 10 10 10 10 10 10 (10 10 10) (10 10 10) 22 32 62 2 2 3 3 (2 3) (2 3) 22 54 502 2 2 5 5 5 5 (2 5 5) (2 5 5) 73 7 492 7 7 7 7 (7 7) (7 7) 5 72 5 352 5 7 7 5 (5 7) (5 7) 6 24 6 242 6 2 2 2 2 6 (6 2 2) (6 2 2) 102 5 (2 5) 2 (5 2) (5 2) 5 10 2 6 23 3 122 (3 2) 2 2 2 3 (2 2 3) (2 2 3) 152 25 752 (5 3) (5 3) (5 5) (5 5 3) (5 5 3) 802 (4 2) 5 4 (10 2 2) (4 2 10) (4 2 10) 8 5 4 40
Put a box around all of the expressions that are shy squares. Put these numbers in ascending order without calculating their value. Shy Squares 33 64 3 32 64 8 35 64 4 33 64 4 32 64 4 35 64 8 34 64 3 38 64 82 3 64 12 38 64 83 35 64 3 3 64 36 38 64 43 38 64 4
Put a box around all of the expressions that are shy squares. Put these numbers in ascending order without calculating their value. Shy Squares 33 64 3 32 64 8 35 64 4 33 64 4 32 64 4 35 64 8 34 64 3 38 64 82 3 64 12 38 64 83 35 64 3 3 64 36 38 64 43 38 64 4
Put a box around all of the expressions that are shy squares. Put these numbers in ascending order without calculating their value. Shy Squares 32 64 4 = 3 64 12 32 64 8 35 64 3 35 64 4 33 64 3 34 64 3 = 35 64 8 33 64 4 3 64 36 38 64 4 38 64 82 38 64 43 = 38 64 83
Use what you know about related calculations to calculate the following square roots. 0.0081 = 2.25 = 0.49 = 810 000 = 10000 = 0.01 = 0.000036 = 25 000 000 = 1.96 = 1.69 = 0.0196 = 169 000 000 = 1 960 000 = 0.0121 =
Use what you know about related calculations to calculate the following square roots. 0.0081 = 0.09 2.25 = 1.5 0.49 = 0.7 810 000 = 900 10000 = 100 0.01 = 0.1 0.000036 = 0.006 25 000 000 = 5000 1.96 = 1.4 1.69 = 1.3 0.0196 = 0.14 169 000 000 = 13 000 1 960 000 = 1400 0.0121 = 0.11
82 150 81 < 82 < 100 144 < 150 < 169 9 < 82 < 10 12 < 150 < 13
82 150 81 < 82 < 100 144 < 150 < 169 9 < 82 < 10 12 < 150 < 13 3 200 90 40 190 2
82 150 81 < 82 < 100 144 < 150 < 169 9 < 82 < 10 12 < 150 < 13 1 < 3 < 2 14 < 200 < 15 3 200 90 40 9 < 90 < 10 6 < 40 < 7 13 < 190 < 14 190 2 1 < 2 < 2
Write the correct inequality symbol in each circle 16 + 9 16 + 9 25 + 5 30 160 12 15 + 16 16 + 16 15 + 17 16 + 16 15 200 15 3 16 3 15 250 15 3 16 4 20 5
Write the correct inequality symbol in each circle < > 16 + 9 16 + 9 25 + 5 30 > < 160 12 15 + 16 16 + 16 > > 15 + 17 16 + 16 15 200 < < 15 3 16 3 15 250 < > 15 3 16 4 20 5
< 121 100.000001 101 115 120.99999 100 < < 11 10 < 100.000001 101 115 120.99999 110.5 is the midpoint of 100 and 121. 100 110.5 121 Is 110.5 the midpoint of 100 and 121? 10.52= 100 5 110.25 10000 500 + + + 100 10000 500 10.52 110.25 = 10.5 500 25 5 500 25 110.25 110.5 11025
64.0 64 + 0 64 1 264 82= 64 = 8 64 = 43= 64 364 = 4 364 3 64 3 6 4
Find the edge length of each square or cube given the area or volume. 196??2 64??2 27??3 64??3 8?3 125?3 121??2 49??2
Find the edge length of each square or cube given the area or volume. 225??2 64??3 27??3 1?3 81?2 216??3 0.125?3 400??2
Find the edge length of each square or cube given the area or volume. 14?? 9?? 196??2 64??2 27??3 8?? 2? 64??3 8?3 4?? 125?3 121??2 5? 49??2 7?? 11??
Find the edge length of each square or cube given the area or volume. 15?? 3?? 225??2 64??3 27??3 4?? 1?3 81?2 1? 9? 216??3 0.125?3 6?? 400??2 0.5? 20??