[PDF] DOWNLOAD READ Diagnosis Solving the Most Baffling Medical Mysterie
\"[PDF] Download Diagnosis: Solving the Most Baffling Medical Mysteries Ebook | READ ONLINE\nDownload File => https:\/\/greatebook.club\/?book=0593136632\nDownload Diagnosis: Solving the Most Baffling Medical Mysteries read ebook Online PDF EPUB KINDLE\nDiagnosis: Solving the Most Baffling Medical M
3 views • 1 slides
Understanding Bernoulli's Equation in Fluid Mechanics
Bernoulli's equation, a fundamental principle in fluid dynamics, relates pressure, kinetic energy, and potential energy of a fluid flowing in a pipe. Through examples and explanations, explore how this equation can be used to calculate velocity, pressure differences, and forces in various scenarios
1 views • 12 slides
Thermodynamics of Solar Plasma: SAHA-S Equation of State and Recent Results
SAHA-S equation of state (EOS) presents the current state and recent results in thermodynamics of solar plasma. Key authors V.K. Gryaznov, A.N. Starostin, and others have contributed to this field over 20 years. The equilibrium composition between 145 species, including elements and all ions, is exp
1 views • 23 slides
Overview of Fluid Mechanics: Branches, Flow Types, and Equations
Fluid mechanics is subdivided into three branches: Fluid Static, Kinematics, and Hydrodynamics. The study of fluid flow includes different types such as uniform, non-uniform, steady, and unsteady flow. The motion of fluid particles obeys Newton's laws, and the conservation of mass and energy plays a
1 views • 4 slides
Engaging Paper-Based Problem Solving for Computational Thinking Skills
Implementing paper-based problem-solving activities using puzzles, riddles, and pattern recognition can effectively introduce computational thinking without the need for complex technology or terminology. Through real-life scenarios like transporting a fox, chicken, and corn across a river or encodi
0 views • 23 slides
Understanding Waveguiding Systems and Helmholtz Equation in Microwave Engineering
Waveguiding systems are essential in confining and channeling electromagnetic energy, with examples including rectangular and circular waveguides. The general notation for waveguiding systems involves wave propagation and transverse components. The Helmholtz Equation is a key concept in analyzing el
2 views • 50 slides
Understanding Thermodynamics and Fluid Mechanics Fundamentals for Efficiency
Explore key concepts in thermodynamics and fluid mechanics such as the equation of continuity, the first law of thermodynamics, the momentum equation, Euler's equation, and more. Learn about efficiency, internal energy, and the laws governing energy transfer in various systems. Delve into topics lik
2 views • 12 slides
Understanding Economic Forecasting with Simulation Models
Explore the concept of economic forecasting using multi-equation simulation models, focusing on producing data that follows estimated equations rather than estimating model parameters. Learn about endogenous and exogenous variables, the importance of assumptions in forecasting, and the use of simula
0 views • 38 slides
Balancing Chemical Equations Using Algebraic Solving Method
Learn how to balance chemical equations using the algebraic solving method step-by-step by assigning variables to compounds and solving for each variable. This comprehensive guide takes you through the entire process, from assigning variables to simplifying fractions and substituting values back int
1 views • 9 slides
Understanding the Hammett Equation in Chemical Reactions
The Hammett equation explores how substituents influence the dissociation of benzoic acid, affecting its acidity. By quantifying this influence through a linear free energy relationship, the equation helps predict the impact of substituents on different processes. Through parameter definitions and m
0 views • 9 slides
Introduction to Dynamic Structural Equation Modeling for Intensive Longitudinal Data
Dynamic Structural Equation Modeling (DSEM) is a powerful analytical tool used to analyze intensive longitudinal data, combining multilevel modeling, time series modeling, structural equation modeling, and time-varying effects modeling. By modeling correlations and changes over time at both individu
0 views • 22 slides
Understanding Separation Columns in Chemical Engineering
Explore the world of separation columns including distillation, absorption, and extraction, along with empirical correlations, minimum number of stages, Fenske equation, Underwood equation, Kirkbride equation, examples, and solutions presented by Dr. Kh. Nasrifar from the Department of Chemical and
5 views • 15 slides
Solving Combination Circuits: Practice and Problem-Solving
Explore solving combination circuits through practice exercises and class problem-solving techniques involving equivalent resistance determination, PIER chart application, Kirchhoff's laws, current and voltage analysis, and power dissipation calculations. Enhance your understanding of circuit analys
3 views • 26 slides
Comprehensive Overview of Freezing Time Methods in Dairy Engineering
Neumann, Tao, and Non-Dimensional methods are key approaches for determining freezing times in unsteady state heat transfer processes in dairy engineering. The Neumann Problem, Tao Solutions, and Cleland and Earle Non-Dimensional Equation offer distinct equations and models to calculate freezing tim
1 views • 8 slides
Understanding Matrices and Solving Equations in Electrical Engineering
Matrices play a crucial role in solving linear equations in Electrical Engineering applications. Learn about matrix structures, special matrices, inverses, transposes, system of linear equations, and solving methods using MATLAB/Python. Explore the application of matrices in solving voltage-current
1 views • 24 slides
Introduction to Quantum Mechanics: Energy Levels and Schrödinger Equation
Quantum mechanics reveals that all systems possess discrete energy levels, determined by solving the Schrödinger equation where the Hamiltonian operator represents total energy. In a particle-in-a-box scenario, potential energy is infinite outside the box. The Schrödinger equation simplifies to a
0 views • 12 slides
Fundamental Comparison: Wheeler-DeWitt vs. Schrödinger Equation
The debate on whether the Wheeler-DeWitt equation is more fundamental than the Schrödinger equation in quantum gravity remains inconclusive. While the Wheeler-DeWitt equation presents an elegant formulation, the Schrödinger equation is essential in specific cases. The issue of time and coordinate
0 views • 6 slides
Fun Algebraic Thinking Activities for Learning
Engage in a series of interactive algebraic thinking activities to enhance your problem-solving skills. From true or false equations to solving open sentences, these sponge activities will challenge and strengthen your mathematical reasoning abilities. Explore different identities and test your know
0 views • 27 slides
Understanding Open Channel Flow and Mannings Equation
This review covers hydraulic devices such as orifices, weirs, sluice gates, siphons, and outlets for detention structures. It focuses on open channel flow, including uniform flow and varied flow, and explains how to use Mannings equation for calculations related to water depth, flow area, and veloci
1 views • 43 slides
Exploring Membrane Potential Densities and the Fokker-Planck Equation in Neural Networks
Delve into the concepts of membrane potential densities and the Fokker-Planck Equation in neural networks, covering topics such as integrate-and-fire with stochastic spike arrival, continuity equation for membrane potential density, jump and drift flux, and the intriguing Fokker-Planck Equation.
0 views • 29 slides
Problem Solving with Quadratic Functions in Real Life Situations
Quadratic functions play a key role in solving real-life problems. This content explores finding the equation of a quadratic function in scenarios such as determining the time taken for a rocket to reach its maximum height, finding the maximum height reached by the rocket, and calculating the time i
0 views • 16 slides
Leapfrog Scheme for Advection Equation
The provided images illustrate the Leapfrog scheme applied to an advection equation, focusing on the center method in time and space. The stability of the method is analyzed with assumptions regarding the behavior of the solution. Through the exploration of Courant numbers and CFL conditions, the st
0 views • 25 slides
Numerical Solution of Eulerian Advection Equation in 1-D Operator Splitting
Application of operator splitting over three directions allows reducing the Eulerian advection equation to 1-D, enabling finite differencing of derivatives while maintaining conservation properties. Various numerical schemes like forward Euler, leapfrog, and linear upstream are discussed, highlighti
0 views • 8 slides
The Importance of Problem-Solving Skills in Everyday Life
Developing effective problem-solving skills is crucial as they play a significant role in various aspects of our daily lives, from simple tasks to complex challenges. This article explores the significance of problem-solving, provides strategies like algorithms and heuristics, discusses obstacles en
0 views • 34 slides
Excel Tutorial: Finding Trendline Equation and Calculating Rates of Change
Learn how to find the equation of a trendline in Excel and use it to calculate rates of change. This step-by-step guide includes importing data, adding a trendline, displaying the equation, and interpreting it for analysis. Make the most of Excel's features for data analysis.
0 views • 11 slides
Enhancing Creativity and Problem Solving Techniques
Explore key outcomes in fostering creativity, identifying and removing blocks to problem-solving, and understanding the process of generating new ideas through concepts like creativity vs critical thinking and block-busting. Learn strategies including brainstorming, defer judgment, and morphological
0 views • 15 slides
Linearized Boltzmann Equation in Statistical Mechanics
This lecture delves into the linearized Boltzmann equation and its applications in studying transport coefficients. The content covers the systematic approximation of transport coefficients, impact parameters of collisions, and the detailed solution for a dilute gas system. It explores the notation
0 views • 25 slides
Quantum Chemistry Learning Goals and Concepts
This content covers the learning goals and concepts of quantum chemistry leading up to the Schrodinger equation and potential energy wells, excluding the material on the hydrogen atom introduced later. It explores models of the atom, including observations of atomic spectra, the Bohr model, de Brogl
0 views • 22 slides
Enhancing Problem-Solving Skills in Mathematics Workshops
In this workshop focused on problem-solving in mathematics, participants engage in various tasks and activities to develop a deep understanding of problem-solving strategies. The key messages emphasize the importance of integrating problem-solving into daily mathematics learning, utilizing multiple
0 views • 34 slides
Analytical Solutions for 2D Heat Equation with Separation of Variables
Consider the steady-state 2D heat equation with constant thermal conductivity. Analyze analytical solutions using separation of variables method for a square plate with defined boundary conditions. Learn how to express the general form of solutions and apply them to the heat equation in Cartesian ge
0 views • 15 slides
Grade 7 Math Sample Questions
Explore sample Grade 7 math questions on communication, reasoning, and problem-solving. Topics include rational numbers, prime numbers, shopping decisions, and equation solving. Practice your math skills with these interactive questions and answer rubrics.
0 views • 33 slides
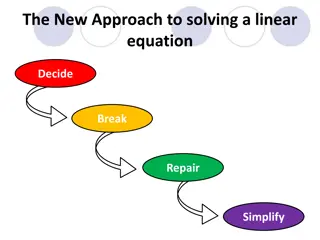
New Approach to Solving Linear Equations: Deciding, Breaking, Repairing, Simplifying
In the new approach to solving linear equations, the process involves deciding on the steps to take, breaking down the equation, repairing any mistakes, and simplifying to find the solution. Illustrations guide you through each step, from decision-making to final resolution. The method aims to make
0 views • 69 slides
Dynamic Function for Basal Area of Trees Derived from Differential Equation
Mathematical methods presented by Braun and Simmons are used to derive a dynamic function for the basal area of individual trees from a production-theoretically motivated autonomous differential equation. The differential equation and general dynamic function are described, highlighting the relation
0 views • 45 slides
Computational Earth Science: Solving Heat Flow in Objects with Complex Shapes Using Finite Difference Method
Explore projects involving the Finite Difference Method for solving static heat conduction problems, also known as the Poisson Equation. Topics include testing boundary conditions, symmetry of solutions, point sources, dipoles, and more. Gain insights into changing boundary conditions and understand
0 views • 20 slides
Understanding Circles in Analytic Geometry
Explore the fundamentals of circles in analytic geometry by learning how to derive circle formulas, equation determination, completing the square, proving circle properties, and solving application problems. Discover the definition of a circle, its relation to triangles, and the terms, equations, an
0 views • 51 slides
Analysis and Comparison of Wave Equation Prediction for Propagating Waves
Initial analysis and comparison of the wave equation and asymptotic prediction of a receiver experiment at depth for one-way propagating waves. The study examines the amplitude and information derived from a wave equation migration algorithm and its asymptotic form. The focus is on the prediction of
0 views • 23 slides
Solving Multi-Step Equations: Simplify, Solve, and Check
As equations become more complex, follow steps to simplify each side of the equation and use inverse operations to solve. Examples and the distributive property are provided to help understand the process better. Always remember to check that both sides of the equation are simplified before solving
0 views • 22 slides
Understanding the Photoelectric Effect and Einstein's Equation
The photoelectric effect is explained by Einstein through assumptions of photons and their interaction with electrons on a metal surface. The maximum kinetic energy of ejected electrons depends on the frequency of incident radiation, as shown in Einstein's Equation. The greater the frequency, the hi
0 views • 6 slides
Graphical Solution of Equations Using GDC - Step-by-Step Guide
Learn how to solve equations graphically using a Graphic Display Calculator (GDC) with step-by-step instructions. Turn on the GDC, input the equation on Y1 and Y2, draw the graphs, and find the intersection point to determine the x-value. An example equation, 2x + 8 = x + 1, is solved using this met
0 views • 20 slides
Solving Quadratic Equations Using a GDC
Understanding quadratic equations and their solutions using a graphing calculator. Learn about the general form of quadratic equations, how to rearrange them, and apply the Null Factor Law to solve for roots. Utilize examples and step-by-step instructions to solve quadratic equations using a GDC, in
0 views • 22 slides
![[PDF] DOWNLOAD READ Diagnosis Solving the Most Baffling Medical Mysterie](/thumb/9855/pdf-download-read-diagnosis-solving-the-most-baffling-medical-mysterie.jpg)