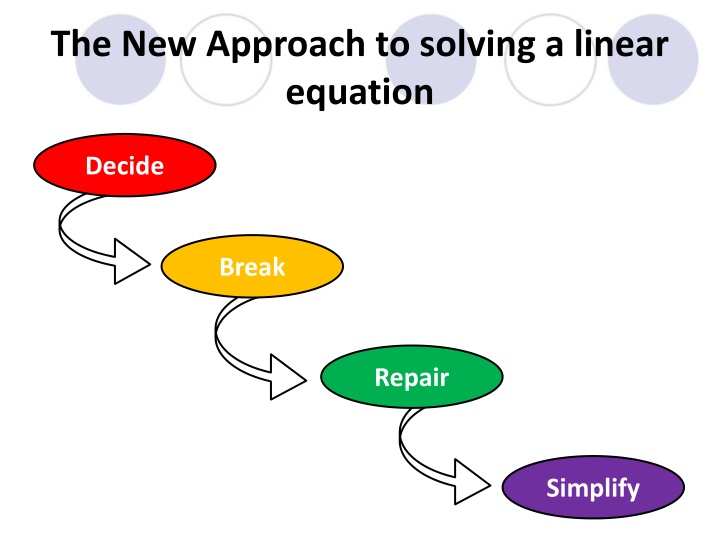
New Approach to Solving Linear Equations: Deciding, Breaking, Repairing, Simplifying
In the new approach to solving linear equations, the process involves deciding on the steps to take, breaking down the equation, repairing any mistakes, and simplifying to find the solution. Illustrations guide you through each step, from decision-making to final resolution. The method aims to make solving linear equations more accessible and understandable.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
The New Approach to solving a linear equation Decide Break Repair Simplify
Decide how to get to ?. ? + 1 ?
Decide how to get to ?. ? + 5 ?
Decide how to get to ?. ? + 3 ?
Decide how to get to ?. ? 3 +?
Decide how to get to ?. ? 10 +??
Decide how to get to ?. ? 6 + ?
Break Do you agree with the following? ? + ? = ?? ? + ? + ? = ?? + ? ? + ? + ? ???? = ?? + ? ???? ? + ? + ? ???? + ? = ?? + ? ???? The last step is what is known as breaking because the calculation on the left is not equal to calculation on the right. So they are not equal. How do I repair this mistake?
Worked example Your turn Solve ? + 1 = 25. Solve ? + 2 = 45. Solve ? 6 = 20. Solve ? 7 = 49.
Solve the following equations: ? = 1 ? + 5 = 11 7 + ? = 8 ? = 6 ? = 1 5 + ? = 11 9 + ? = 8 ? = 6 ? = 18 7 = ? + 6 9 + ? = 9 ? = 1 ? = 9 7 = ? 6 9 + ? = 0 ? = 13 9 + ? = 0 ? = 9 9 = ? 2 ? = 11 9 + ? =1 ? = 91 9 = ? 3 ? = 12 2 2 9 = ? 5 ? = 14 ? 9 =1 ? = 91 2 2 9 = ? 5 ? = 4 ? + 9 =1 ? = 91 9 = 5 + ? ? = 4 2 2
Decide how to get to ?. 21? ??
Worked example Your turn Solve 5? = 25. Solve 9? = 45. Solve 4? = 20. Solve 7? = 49.
Solve the following equations: ? = 5 48 = 4? ? = 12 4? = 20 ? = 4 4? = 48 ? = 12 4? = 16 ? = 7/4 8? = 48 ? = 6 4? = 7 ? = 3 8? = 56 ? = 7 4? = 12 ? = 11 44 = 4?
Decide how to get to ?. ? 5 ?
Decide how to get to ?. ? 3 ?
Decide how to get to ?. ? 3 ?
Worked example Your turn Solve ? Solve ? 4= 25. 6= 7. Solve ? Solve ? 2= 4. 3= 8. Solve ? Solve ? 3= 3. 5= 6.
Solve the following equations: ? 3= 7 21 = ? ? = 84 ? = 5 4 7 =? 21 = ? 3 5 ? = 105 ? = 4 7 =? 21 =? ? = 105 ? = 7/4 3 5 7 = ? 6 =? ? = 30 ? = 3 3 5 21 = ? 6 7 =? ? = 65 ? = 11 3 5
Decide how to get to 2?. 2? + 1 ?
Decide how to get to 2?. 2? 3 +?
Decide how to get to 5?. 5? 7 +?
Decide how to get to 5?. 5? + 3 ?
Worked example Your turn Solve 2? + 12 = 30. Solve 2? + 8 = 30. Solve 12 4? = 44. Solve 16 4? = 44.
Solve the following equations: ? = 20 ? = 9 2? + 5 = 35 2? + 3 = 21 ? = 20 ? = 9 5 2? = 35 3 + 2? = 21 ? = 15 5 2? = 35 ? = 12 2? 3 = 21 ? = 14 7 2? = 35 ? = 9 3 2? = 21 7 4? = 35 ? = 7 ? = 8 5 2? = 21 7 7? = 35 ? = 4 ? = 8 2? + 5 = 21
Getting rid of brackets 3 ? + 2 = 9 Just expand! After this, carry on as before. 3? + 6 = 9
Your turn Worked example 3 ? + 8 = 48 3 ? + 6 = 48
Solve the following equations: 4(? + 8) = 40 5(? 8) = 80 ? = 2 ? = 48 ? = 12 ? = 48 2 ? + 8 = 40 80 = 5(? 8) ? = 16 ? = 24 2 ? + 8 = 48 80 = 5(2? 8) 2 ? + 8 = 48 120 = 5(2? 8) ? = 32 ? = 34 120 = 5(2? 6) ? = 16 ? = 16 2 ? 8 = 48 120 = 5(2? 6) ? = 32 ? = 27 2 ? 8 = 48
Decide how to get to 1 by adding or subtracting. 2? + 1 ??
Decide how to get to 3 by adding or subtracting. 2? 3 ??
Decide how to get to 7 by adding or subtracting. 5? 7 ??
Decide how to get to 3 by adding or subtracting. 5? + 3 ??
Decide how to get to 1 by adding or subtracting. 1 2? +??
Decide how to get to 3 by adding or subtracting. 3 2? +??
Decide how to get to 7 by adding or subtracting. 7 5? +??
Decide how to get to 3 by adding or subtracting. 3 5? +??
Decide how to get to 7 by adding or subtracting. 7 7? +??
Decide how to get to 3 by adding or subtracting. 3 7? +??
Example by Fading Reflection Your Turn Worked Example Solve Solve Why did I subtract 2? from each side? Solve 5? + 7 = 2? + 22 Decide( 2?) Repair and Simplify Equation 5? + 7 = 3? + 23 5? + 7 = 2? + 31 Why did I not subtract 5? from each side? How many DBRS processes are there? ? = ? 5? + 7 2? = 2? + 22 2? Simplify 3? + 7 = 22 Solve Solve Solve Why did I add ? to each side? 2? 23 = 9 2? Decide(+2?) Repair and Simplify Equation 2? 23 = 7 ? 2? 23 = 12 3? Why did I not subtract 2? from each side? ? = ? 2? 23 + 2? = 9 2? + 2? Simplify How many DBRS processes are there? 4? 23 = 9
Questions Solve the following equations: ? = ? ? = ? 1) 5? + 7 = 2? + 13 8) 6? + 11 = 3? 4 ? = ? ? = ? 2) 9? + 5 = 7? + 15 9) 6? + 19 = 10? 5 ? = ? ? = ? 3) 7? + 3 = 2? + 28 10) 8? 7 = 3? 32 ? = ?? ? = ? 4) 10? + 19 = 9? + 9 11) 7 2? = 23 4? ? = ? ? = ?? 5) 7? + 33 = 4? + 18 12) 2 5? = 110 14? ? = ? ? = ? 6) 3? + 85 = 12? + 4 13) 3 6? = 7 2? ? = ? ? = ? 7) 2? + 21 = 6? + 5 14) 17 18? = 81 10? Why is it not possible to solve the following? Explain your answer clearly! 2? + 3 = 10 + 2?
Example by Fading Reflection Your Turn Worked Example Solve 7 ? 3 = 2(? + 7) Expand 7? 21 = 2? + 14 Solve 9 ? 3 = 4(? + 7) What do I need to remember with brackets? Solve 3 ? + 2 = 2(? + 3) Why did I subtract 2?? ? = ?? Decide( 2?) Repair and Simplify Equation 7? 21 2? = 2? + 14 2? How many DBRS processes are there? Simplify 5? 21 = 14 Solve 3 ? 5 1 = 5(? + 6) Expand 3? 15 1 = 5? + 30 Simplify 3? 16 = 5? + 30 Solve 7 ? + 6 7 = 4(? + 2) What do I need to remember with brackets? Solve 3 ? + 5 7 = 2(? + 2) What did I do with the 7? ? = ? Decide( 3?) Repair and Simplify Equation Why did I subtract 2?? 3? 16 3? = 5? + 30 3? How many DBRS processes are there? Simplify 16 = 2? + 30
Questions Solve the following equations: 7) 3 ? 5 5 = 5 ? + 6 1) 3 ? + 3 = 3 2? 4 ? = ?? ? = ?/? 8) 7 ? + 6 1 = 4(? + 2) 2) 2 3 + ? = 3 2? 4 ? = ?/? ? = ?? 9) 6 ? + 2 = 24 3 ? 5 3) 2 3 + ? = 3(2? 4) ? = ?/? ? = ? ? = ? 10) 5 6 ? 3 = 5 3(? 2) 4) 2 3 + ? = 3 2? 4 ? = ?/? 5) 3 3 ? = 3 2? 4 ? = ? 6) 3 3 ? = 6(2? 4) ? = ? Explain your thinking process to solve the equation ? 4 1 = 3(2? 11).
Example by Fading Reflection Your Turn Worked Example Solve 3 ? 3 + 4 2? 6 = 110 Solve 5 ? + 3 + 2 2? 6 = 111 Why do I separate the + 3(2? + 6) ? Solve 8 ? + 3 + 3 2? + 6 = 84 Expand 5? + 15 + 4? 12 = 111 Simplify 9? + 3 = 111 What do I need to remember with brackets? ? = ?? How many DBRS processes are there? Solve 3 ? 3 4 2? 6 = 110 Solve 5 ? 3 2 2? 6 = 111 Why do I separate the 3(2? 6) ? Solve 8 ? + 3 3 2? 6 = 84 Expand 5? 15 4? + 12 = 111 Simplify ? 3 = 111 What do I need to remember with brackets? ? = ?? How many DBRS processes are there?
Questions Solve the following equations: 4) 2 2? 1 4 3? 1 = 16 1) 2 ? + 3 + 4 ? + 1 = 22 ? = ? ? = ? 5) 5 2? + 3 6 ? 1 = 29 2) 7 ? 3 + 5 ? + 2 = 37 ? = ? ? = ? 6) 4 5? 2 6 3? 1 = 12 3) 3 ? 2 + 2 ? 5 = 14 ? = ? ? = ? The perimeter of the rectangle is equal to 3 times the perimeter of the triangle. Calculate the value of ?. 2? + 7 ?? ? + 2 ?? ? = ? ??? 3? 4 ?? (? + 1)??
