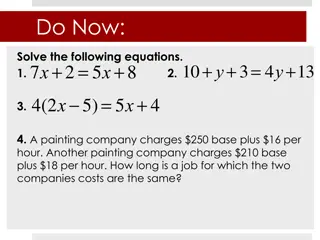Solving Multi-Step Equations: Simplify, Solve, and Check
As equations become more complex, follow steps to simplify each side of the equation and use inverse operations to solve. Examples and the distributive property are provided to help understand the process better. Always remember to check that both sides of the equation are simplified before solving it.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Multi-Step Equations Return to Table of Contents Return to Table of Contents
Steps for Solving Multiple Step Equations As equations become more complex, you should: 1. Simplify each side of the equation. (Combining like terms and the distributive property) 2. Use inverse operations to solve the equation. Remember, whatever you do to one side of an equation, you MUST do to the other side!
Examples: -15 = -2x - 9 + 4x -15 = 2x - 9 +9 +9 -6 = 2x 2 2 -3 = x Combine Like Terms Undo Subtraction first Touch to reveal answer Undo Multiplication second 7x - 3x - 8 = 24 4x - 8 = 24 + 8 +8 4x = 32 4 4 x = 8 Combine Like Terms Undo Subtraction first Touch to reveal answer Undo Multiplication second
Now try an example. Each term is infinitely cloned so you can pull them down as you solve. -7x -7x -7x -7x -7x -7x = -6 + 3 + 6x + 3 + 3 + 3 + 3 + 6x + 6x + 6x -6 -6 -6 -6 -6 ans wer
Now try another example. Each term is infinitely cloned so you can pull them down as you solve. = 44 6x 6x 6x 6x 6x 6x 6x + x + x + x + x + x - 5 - 5 - 5 - 5 - 5 - 5 44 44 44 44 ans wer
Always check to see that both sides of the equation are simplified before you begin solving the equation. Sometimes, you need to use the distributive property in order to simplify part of the equation.
Distributive Property For all real numbers a, b, c a(b + c) = ab + ac a(b - c) = ab - ac
Examples 5(20 + 6) = 5(20) + 5(6) 9(30 - 2) = 9(30) - 9(2) 3(5 + 2x) = 3(5) + 3(2x) -2(4x - 7) = -2(4x) - (-2)(7)
Examples: 5(1 + 6x) = 185 5 + 30x = 185 Distribute the 5 on the left side -5 -5 Undo addition first 30x = 180 30 30 Undo multiplication second x = 6 Move to reveal answer 2x + 6(x - 3) = 14 2x + 6x - 18 = 14 8x - 18 = 14 +18 +18 8x = 32 8 8 x = 4 Distribute the 6 through (x - 3) Combine Like Terms Undo subtraction Move to reveal answer Undo multiplication
Now show the distributing and solve 5 ( -2 + 7x ) = 95
Now show the distributing and solve 6 ( -2x+ 9 ) = 102
23 Solve. 3 + 2t + 4t = -63
24 Solve. 19 = 1 + 4 - x
25 Solve. 8x - 4 - 2x - 11 = -27
26 Solve. -4 = -27y + 7 - (-15y) + 13
27 Solve. 9 - 4y + 16 + 11y = 4
28 Solve. 6(-8 + 3b) = 78
29 Solve. 18 = -6(1 - 1k)
30 Solve. 2w + 8(w + 3) = 34
31 Solve. 4 = 4x - 2(x + 6)
32 Solve. 3r - r + 2(r + 4) = 24
33 What is the value of p in the equation 2(3p - 4) = 10? A B C D 1 2 1/3 3 1/3 From the New York State Education Department. Office of Assessment Policy, Development and Administration. Internet. Available from www.nysedregents.org/IntegratedAlgebra; accessed 17, June, 2011.
