Understanding Radians: A Challenge in Measurement Units
Explore the concept of radians as a unit for measuring angles through challenges involving arc lengths, radius comparisons, and conversions to degrees. Dive into a word search activity to test your knowledge and understanding of radians vs. degrees.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Week 4 3 problems to work through this week! Answers to weeks 2 and 3 coming next week!
Challenge 1: Radians We can measure distances using several different units. For example, centimetres or inches. Look at the two sides of this ruler.
Challenge 1: Radians We can also measure angles using different units. We usually use degrees, but another unit for measuring angles is radians. Look at these different protractors. We will have a look at how radians work in this challenge . ? ? ? ?
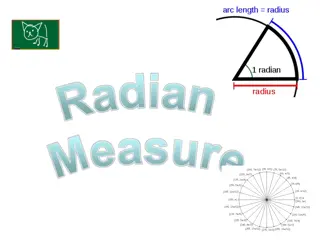
What do you notice about these sectors? What is the same? What is different? In each diagram, the arc length is the same as the radius. There is only 1 angle at which this happens, either 57.3 or 1 radian! This is how a radian is defined.
Challenge 1: Radians 1 radian is much bigger than 1 degree. Much in the same way as 1 mile is longer than 1 kilometre. As we have just seen, 1 radian is a special angle because it s the angle which makes the arc length the same as the radius. (In degrees it s 57.3 which isn t very memorable!) If half a turn is 180 , this is the same as 3.14159265359 radians. Recognise this number? Yes it s pi or . So 180 = radians. So in a full turn, 360 ,we have 2 radians.360 = 2 radians. Mathematicians quite like radians as we really like ! We can either use a little c or rads to show what units we are using. One of the easiest conversions to remember is: 180 = ?? or 180 = ? rads So, we can use fractions of to represent other angles e.g. 90 =? 2rads
Challenge 1: Radians Wordsearch Fill in the blanks to make the statement correct and then find that word in the wordsearch. Z L F B S T N Q R N Question 57.3o = 1 _ _ _ _ _ _ _ X P Z X I G X U A Q Pi radians = _ _ _ hundred and eighty degrees S X Z C X D O I M U Two pi radians = Three hundred and _ _ _ _ _ degrees One _ _ _ _ _ _ _ pi radians = 90o E I O W T F D F U A One _ _ _ _ _ pi radians = 60o P E X Z H A N I Y R _ _ _ thirds pi radians = 120o _ _ _ _ _ quarters pi radians = 135o P I R T R O N E T T ? 2rads = _ _ _ _ _ _ degrees O Q Q H Y M Q H E E _ _ _ _ pi radians = Seven hundred and twenty degrees Three pi radians = _ _ _ _ hundred and forty degrees F I V E T S I U N R One _ _ _ _ _ pi radians = 30o T K D E G R E E I I ? 180rads = one _ _ _ _ _ _ O K O Y D I A A N J Put your answer on the Desmos activity (page 2) .
Challenge 1: Radians The horizontal axis on the graph of ? = ??? ? below has got muddled! Drag the red labels into the correct positions! Complete on the Desmos activity (page 3) .
Challenge 2: The Curious Incident of the Dog In the Sherlock Holmes story Sliver Blaze the question is asked: Is there any other point to which you would wish to draw my attention? To the curious incident of the dog in the night-time The dog did nothing in the night-time That was the curious incident remarked Sherlock Holmes 1, 2, 4, 7, 11, 14, 16, 17, 19, 22, 26, 28, 29, 41, 44, ? What is next in the sequence? Think about what Sherlock remarked. Hint: Do not think about which numbers are included. [Credit: Professor Stewart s Hoard of Mathematical Treasures] Put your answer on the Desmos activity (page 4) .
Challenge 3: Digits! Using the following digits, make 100. Rules: No changing the order of the digits. No subtraction allowed. No concatenation of digits. e.g. you cannot use 2 and 3 to make 23. 1 2 3 4 5 6 7 8 9 = 100 [Credit: Professor Stewart s Hoard of Mathematical Treasures] Put your answer on the Desmos activity (page 5) .