Understanding Linear Regression: Concepts and Applications

Linear regression is a statistical method for modeling the relationship between a dependent variable and one or more independent variables. It involves estimating and predicting the expected values of the dependent variable based on the known values of the independent variables. Terminology and notation, conditional mean calculations, population regression curves, simple regression concepts, and linear function parameter functions are discussed in detail in the context of regression analysis.

• Linear Regression
• Statistical Modeling
• Dependent Variable
• Independent Variable
• Regression Analysis

noe Follow

Uploaded on Aug 05, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

Presentation Transcript

1. Linear Regression Summer School IFPRI Westminster International University in Tashkent 2018

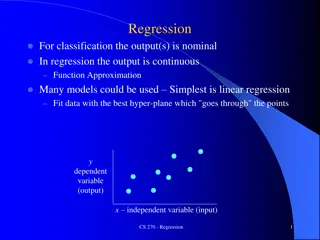
2. Regression Regression analysis is concerned with the study of the dependence of one variable, the dependent variable, on one or more other variables, the explanatory variables, with a view of estimating and/or predicting the population mean or average values of the former in terms of the known or fixed (in repeated sampling) values of the latter. 2

3. Terminology and Notation Dependent Variable Explained variable Predictand Regressand Response Endogenous Outcome Controlled variable Independent variable Independent variable Predictor Regressor Stimulus Exogenous Covariate Control variable 3

4. Conditional Mean Income 80 100 120 140 160 180 200 220 240 260 Consumption 55 65 79 80 102 110 120 135 137 150 60 70 84 93 107 115 136 137 145 152 65 74 90 95 110 120 140 140 155 175 70 80 94 103 116 130 144 152 165 178 75 85 98 108 118 135 145 157 175 180 88 113 125 140 160 189 185 115 162 191 Total 325 462 445 707 678 750 685 1043 966 1211 65 77 89 101 113 125 137 149 161 173 Conditional mean 4

5. Simple Regression 190 Weekly Consumption Conditional expected values E(Y|X) 170 150 130 110 90 Population Regression Curve 70 50 60 80 100 120 140 160 180 200 220 240 260 280 Weekly Income A population regression curve is simply the locus of the conditional means of the dependent variable for the fixed values of the explanatory variable(s). 5

6. Simple Regression = ( | ) ( ) E Y X f X i i Conditional Expectation Function (CEF) Population Regression Population Regression Function (PRF) = + ( | ) E Y X X 1 2 i i Linear Population Regression Function Regression Coefficients 6

7. Linear Y Y = + + 2 Y X X 1 + = X Y e 1 2 3 2 X X Y Linear in parameter functions 2 = + ( | ) E Y X X 1 2 i i = + + + 2 3 Y X X X 1 2 3 4 Non-linear in parameter function X 7

8. Stochastic specification Y u = ( | ) E = Y X Stochastic error term u X + ) Nonsystematic component i i i ( | Y E Y i i i Systematic component Y + = 1 [ ) i E E X = ( Y E = ( u E + X u 2 i i i E ( u + E 0 ( | ( | )] + = ( | ) E Y Y | X )] ) u | X ) i i i X i X i i i | iX i 8

9. Sample Regression Function SRF1 vs SRF2 190 SRF2 170 y = 0,5761x + 17,17 Weekly Consumption 150 SRF1 130 y = 0,5091x + 24,455 110 90 70 50 60 110 160 210 260 Weekly Income 9

10. Sample Regression Function = + ( | ) E Y X X PRF 1 2 i i = + Y X SRF 1 2 i i Estimate + = + Y X u 1 2 i i i 10

11. Sample Regression Function Y iY = + Y X 1 2 i i iY iu iu iY iY = + ( | ) E Y X X 1 2 i i ( | ) E Y X i ( | ) E Y X i A X X 11 i

12. Assumptions. Linearity. The relationship between independent and dependent variable is linear. Full Rank. There is no exact relationship among any independent variables. Exogeneity of independent variables. The error term of the regression is not a function of independent variables. Homoscedastisity and no Autocorrelation. Error term of the regression is independently and normally distributed with zero means and constant variance. Normality of Error term 12

13. Ordinary Least Squares = = + + = + Y X u Y u 1 2 = i i i i i u Y Y Y X 1 2 i i i i i ) i Y = u ( Y i i , 1 ) i Y 2 = = 2 2 u ( ( ) Y Y X 1 2 i i i i = 2 ( ) ui f 2 13

14. Ordinary Least Squares = + + + 2 2 2 2 2 2 u 2 2 2 Y n X Y X Y X 1 1 2 1 2 i i i i i i i 2 i u ( ) = + = 0 2 2 2 0 n Y X 1 2 i i 1 = n Y X 1 2 i i = Y X 1 2 14

15. Ordinary Least Squares = + + + 2 2 2 2 2 2 2 2 2 u Y n X Y X Y X 1 1 2 1 2 i i i i i i i 2 i ( ) u = + = 2 i 0 2 2 2 0 X X Y X 2 1 i i i 2 2 1 + = 2 i 0 X X Y X 2 1 i i i ) + = 2 i ( ) 0 X X Y Y X 2 X 2 i i i + = 2 i ( 0 X ( X Y Y X n X 2 i i ) 2 = 2 2 X n X X Y n X Y i i i 1 = 2 2 X X X Y X Y ( 2 i i i n n Cov , ) X Y 2 2 = X = Var ( ) Cov ( , ) X Y Var( ) X 15

16. Assumptions Linear Regression Model = + + Y X u 1 2 i i i X values are repeated in sampling X is assumed to be nonstochastic. Zero mean values of disturbance ui = ( | ) 0 E iX u i

17. Assumptions Homoscedasticity or equal variance of ui [ ) | var( = i i u E X u f(u) = = 2 i 2 ( | )] ( | ) E u X E u X i i i i Y X

18. Assumptions f(u) Y Heteroscedasticity | var( u X = 2 i ) iX i

19. Assumptions No autocorrelation between the disturbances = = | cov( , | , ) {[ ( ( )( )] | | }{[ ) j ( )] | } u u X X E E u u E u X X u E u X i j i j i i i j j i = 0 X u i i j Exogeneity. Zero covariance between Xiand ui = cov( , ) 0 X iu i

20. Estimator Coefficient moments n = i X Y i i n = i = = 1 W Y True value i i n = i 2 1 X i 1 X = i W = + Y X u i n Additionally we know that = j i i i 2 X j 1 n n n n = = = = = = + = + = ( ) ) W Y W X u W X W u i i i i i i i i i 1 1 1 1 i i i i n = 2 X i n = = = 1 1 i W X i i 2 n = 1 i X j 1 j n = ) = + ( ( ) ( ) E E E W u i i 1 i

21. Coefficient moments n = i ) = + ( ( ) ( ) E E E W u i i 1 n = i = ( ) 0 E W u According to our Exogenity assumption. (Error term is independent from X variable. i i 1 Thus, OLS estimator is unbiased estimator.

22. Coefficient moments n = i = + W u i i 1 ( ) n = i ) = = + = 2 2 ( ( ) ( ) Var E E W u i i 1 n n n = i = i i 2 = + = 2 2 ( ) ( 2 ) E W u E W u W W u u i i i i i j i j 1 1 j n n = i i According to Homoscedasticity and no auto-correlation assumptions. 2 + 2 ( ) 2 ( ) W E u W W E u u i i i j i j 1 j

23. Coefficient moments u E ( = ) 2 2 ( ) i According to Homoscedasticity and no auto-correlation assumptions. = 0 E u u i j 1 n = i 2 = W i n = i 2 1 X i 1 2 = ( ) Var n = i 2 X i 1

24. Using similar argument 2 2 = var( ) = ( ) STDEV 2 ( ) Xi X 2 ( ) X X i X X 2 i 2 i X X = 2 = 2 ( ) STDEV var( ) 2 ( ) n X 2 ( ) n X i i 2 = cov( , ) ( ) X 1 2 2 ( ) X X i

25. BLUE estimator 2) = = * 2) ( ( E E 2 2 Sampling distribution of 2 Sampling distribution of 2*

26. OLS Estimation: Multiple Regression Model 2 2 1 + = = ( min i i Y u + + Y X X u 3 3 i i i i 2 2 ) X X 1 2 2 3 3 i i = x Y X X 1 y 2 2 x 3 3 x ( ) x 2 3 ( ) ( )( ) x x y x x = 2 3 x 2 3 i i i i i i i 2 2 2 2 3 2 ( )( ) ( ) 2 3 i i i i ( ) x x 2 2 ( ) ( )( ) y x x y x x x = 3 2 x 2 3 i i i i i i i 3 2 2 2 3 2 ( )( ) ( ) x 2 3 i i i i

27. Assumptions and estimation. Assumptions are the same Minimize the sum of squared residuals The unbiased estimator of R square Adjusted R square = 2 ui 2 n K n n n = = = = + 2 2 2 ( ) ( ) Y Y Y Y u i i i 1 1 1 i i i TSS ESS + RSS X = + ..... Y X X X 0 0 1 1 2 2 i k k RSS 1 N =1 2 R = 2 2 1 1 ( ) R R TSS N k

28. OLS Estimation: Multiple regression model x + x 2 2 2 3 2 3 2 2 1 n 2 X x X x X X x x = + 2 var( ) 2 3 ) 2 3 i i i i 1 2 2 2 3 2 ( x x 2 3 i i i i 2 2 = = var( ) var( ) 2 3 2 2 2 2 3 2 1 ( ) 1 ( ) xi 3 , 2 r xi 3 , 2 r ) 3 , 2 r 2 = cov( , ) 2 3 2 2 2 2 3 1 ( 3 , 2 r x x i i = N 2 ui 2 3

29. Goodness of Fit = + 2 i 2 2 2 i 2 y x i u TSS = ESS + RSS ESS+ RSS = 1 TSS TSS y 2 i x = 2 2 2 ( ) r 2 i

30. Goodness of Fit = + 2 2 i ( u ( ) ) y y y y i i TSS = ESS + RSS ESS+ RSS = 1 TSS TSS 2 y ( ) y y i = 2 R ( ) y i