Conditional and Reference Class Linear Regression: A Comprehensive Overview
In this comprehensive presentation, the concept of conditional and reference class linear regression is explored in depth, elucidating key aspects such as determining relevant data for inference, solving for k-DNF conditions on Boolean and real attributes, and developing algorithms for conditional linear regression. The motivation behind this research, inspired by sub-population risk factors and social science intersectionality, underscores the importance of isolating simple models within specific conditions. The results reveal promising algorithms for addressing these regression challenges.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Conditional and Reference Class Linear Regression Brendan Juba Washington University in St. Louis Based on ITCS 17 paper and joint works with: Hainline, Le, and Woodruff; Calderon, Li, Li, and Ruan. AISTATS 19 arXiv:1806.02326
Outline 1. Introduction and motivation 2. Overview of sparse regression via list- learning 3. General regression via list-learning 4. Recap and challenges for future work
How can we determine which data is useful and relevant for making data-driven inferences?
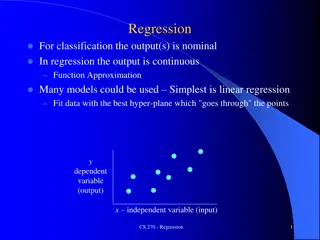
Conditional Linear Regression Given: data drawn from a joint distribution over x {0,1}n, y Rd, z R Find: A k-DNF c(x) Recall: OR of terms of size k terms: ANDs of Boolean literals Parameters w Rd Such that on the condition c(x), the linear rule <w,y> predicts z. z w y c(x) =
Reference Class Regression Given: data drawn from a joint distribution over x {0,1}n, y Rd, z R point of interest x* Find: A k-DNF c(x) Parameters w Rd Such that on the condition c(x), the linear rule <w,y> predicts z and c(x*)=1. z w x* y c(x) =
Motivation Rosenfeld et al. 2015: some sub-populations have strong risk factors for cancer that are insignificant in the full population Intersectionality in social sciences: subpopulations may behave differently Good experimentsisolate a set of conditions in which a desired effect has a simple model It s useful to find these segments or conditions in which simplemodelsfit - And, we don t expect to be able to model all cases simply
Results: algorithms for conditional linear regression We can solve this problem for k-DNF conditions on n Boolean attributes, regression on d real attributes when w is sparse: ( w 0 s for constant s) for all lp norms, loss ( nk/2) for general k-DNF loss ( T log log n) for T-term k-DNF For general coefficients w with -subgaussian residuals, maxterms t of c Cov(y|t) - Cov(y|c) op sufficiently small l2 loss ( T (log log n + log )) for T-term k-DNF Technique: list regression (BBV 08, J 17, CSV 17)
Why only k-DNF? Theorem(informal): algorithms to find w and c satisfying E[(<w,y>-z)2|c(x)] (n) when a conjunction c* exists enable PAC-learning of DNF (in the usual, distribution-free model). Sketch: encode DNF s labels for x as follows Label 1 z 0 (easy to predict with w = 0) Label 0 z has high variance (high prediction error) Terms of the DNF are conjunctions c* with easy z c selecting x with easy to predict z gives weak learner for DNF
Why only approximate? Same construction: algorithms for conditional linear regression solve agnostic learning task for c(x) on Boolean x State-of-the-art for k-DNFs suggests: require poly(n) (n = # Boolean) blow-up of loss, (n) ZMJ 17: achieve (nk/2) blow-up for k-DNF for the corresponding agnostic learning task JLM 18: achieve (T log log n) blow-up for T-term k-DNF Formal evidence of hardness? Open question!
Outline 1. Introduction and motivation 2. Overview of sparse regression via list- learning 3. General regression via list-learning 4. Recap and challenges for future work
Main technique list regression Given examples we can find a polynomial-size list of candidate linear predictors including an approximately optimal linear rule w on the unknown subset S = {(x(j),y(j),z(j)): c*(x(j))=1, j=1, ,m} for the unknown condition c*(x). We learn a condition c for each w, take a pair (w ,c ) for which c satisfies -fraction of data
Sparse max-norm list regression (J. 17) Fix a set of s coordinates i1, ,is. For the unknown subset S, the optimal linear rule using i1, ,is is the solution to the following linear program minimize subject to - wi1xi1 s+1 dimensions optimum attained at basic feasible solution given by s+1 tight constraints (j) + + wisxis (j) - z(j) for j S.
Sparse max-norm list regression (J. 17) The optimal linear rule using i1, ,is is given by the solution to the system wi1xi1 for some j1, ,js+1 S, 1, , s+1 {-1,+1}. Enumerate (i1, ,is,j1, ,js+1, 1, , s+1) in [d]s [m]s+1 {-1,+1}s+1, solve for each w Includes all (j1, ,js+1) Ss+1 (regardless of S!) List has size dsms+12s+1 = poly(d,m) for constant s. (jr) + + wisxis (jr) - z(jr) = r for r = 1, ,s+1
Summary algorithm for max-norm conditional linear regression (J. 17) For each (i1, ,is,j1, ,js+1, 1, , s+1) in [d]s [m]s+1 {-1,+1}s+1, 1. Solve wi1xi1 2. If > * (given), continue to next iteration. 3. Initialize c to k-DNF over all terms of size k 4. For j=1, ,m, if |<w,y(j)> - z(j)| > For each term T in c, if T(x(j))=1 Remove T from c 5. If #{j:c(x(j))=1} > m, ( initially 0) Put = #{j:c(x(j))=1}/m, w =w, c =c (jr) + + wisxis (jr) - z(jr) = r for r = 1, ,s+1 Learn condition c using labels provided by w Choose condition c that includes the most data
Extension to lp-norm list-regression Joint work with Hainline, Le, Woodruff (AISTATS 19) Consider the matrix S = [y(j),z(j)] j=1, ,m:c*(x(j))=1 lp-norm of S(w,-1) approximates lp-loss of w on c Since w* Rd is s-sparse, there exists a small sketch matrix S such that Sv p S v p for all vectors v on these s coordinates (Cohen-Peng 15): moreover, rows of S can be O(1) rescaled rows of S New algorithm: search approximate weights, minimize lp-loss to find candidates for w
lp-norm conditional linear regression Joint work with Hainline, Le, Woodruff (AISTATS 19) Using the polynomial-size list containing an approximation to w*, we still need to extract a condition c such that E[|<w,y>-z|P|c(x)] (n) Use |<w,y(i)>-z(i)|P as weight/label for ith point Easy (T log log n) approximation for T-term k-DNF: only consider terms t with E[|<w,y>-z|P|t(x)]Pr[t(x)] Pr[c*(x)] Greedy algorithm for partial set cover: (terms = sets of points) covering (1- )Pr[c*(x)]-fraction Obtains T log m-size cover small k-DNF c Haussler 88: to estimate T-term k-DNFs, only require m = O(Tk log n) points ( T log log n) loss on c Reference class: add any surviving term satisfied by x*
lp-norm conditional linear regression Joint work with Hainline, Le, Woodruff (AISTATS 19) Using the polynomial-size list containing an approximation to w*, we still need to extract a condition c such that E[|<w,y>-z|P|c(x)] (n) Use |<w,y(i)>-z(i)|P as weight/label for ith point ZMJ 17/Peleg 07: More sophisticated algorithm achieving (nk/2) approximation for general k-DNF (plug in directly to obtain conditional linear regression) J.,Li 19: can obtain same guarantee for reference class
l2-norm conditional linear regression vs. selective linear regression LIBSVM benchmarks. Red: conditional regression; Black: selective regression Bodyfat (m=252, d=14) Boston (m=506, d=13) Space_GA (m=3107, d=6) Cpusmall (m=8192, d=12)
Outline 1. Introduction and motivation 2. Overview of sparse regression via list- learning 3. General regression via list-learning Joint work with Calderon, Li, Li, and Ruan (arXiv). 4. Recap and challenges for future work
CSV17-style List Learning Basic algorithm: Soft relaxation of fitting unknown S Outlier detection and reduction Improve accuracy by clustering output w and recentering We reformulate CSV 17 in terms of terms (rather than individual points) (alternating)
Relaxation of fitting unknown c For fixed weights ( inlier indicators) u(1), ,u(T) [0,1] Each term t has its own parameters w(t) w(1) w(2)w(3) Enclosing ellipsoid Y w(outlier) w(outlier) Solve: minw,Y tu(t)|t|lt (w(t)) + tr(Y) (Y: enclosing ellipsoid; : carefully chosen constant)
Outlier detection and reduction Fix parameters w(1), ,w(T) Rd Give each term t its own formula indicators ct (t) Must find coalition c(t) of -fraction (|c(t)|= t c(t)|t |, = 1/m t c|t|) such that w(t) (t) = 1/|c(t)| t c(t) ct (t)|t |w(t ) w(1) w(2)w(3) (1) (outlier) Intuition: points fit by parameters in small ellipsoid have a good coalition for which objective value changes little (for smooth loss l). Outliers cannot find a good coalition and are damped/removed. w(outlier) Reduce inlier indicator u(t) by 1-|lt(w(t)) - lt( (t))|/maxt |lt (w(t )) lt ( (t ))|-factor
Clustering and recentering Full algorithm: (initially, one data cluster) Basic algorithm on cluster centers Cluster outputs (alternating) Next iteration: run basic algorithm with parameters of radius R/2 centered on each cluster w(1) w(2)w(3) w(j) w(k) w(l)
Overview of analysis (1/3) Loss bounds from basic algorithm Follows same essential outline as CSV 17 Guarantee for basic algorithm: we find such that given w* R, E[l( )|c*]-E[l(w*)|c*] O(R maxw,t c* [ E[lt(w)|t]- E[l(w)|c*] / ) Where [ E[lt(w)|t]- E[l(w)|c*] (w-w*)(Cov(y|t) - Cov(y|c*)) The bound is O(R2maxt c* Cov(y|t) - Cov(y|c*) / ) for all R 1/poly( m/ T) (errors -subgaussian on c*)
Overview of analysis (2/3) From loss to accuracy via convexity We can find: such that given w* R, E[l( )|c*]-E[l(w*)|c*] O(R2 Cov(y|t) - Cov(y|c*) / ) Implies that for all significant t in c*, w(t)-w* 2 O(R2 T maxt c* Cov(y|t) - Cov(y|c*) / ) where is the convexity parameter of l(w) Iteratively reduce R with clustering and recentering
Overview of analysis (3/3) Reduce R by clustering & recentering In each iteration, for all significant t in c*, w(t)-w* 2 O(R2 T maxt c* Cov(y|t) - Cov(y|c*) / ) where is the convexity parameter of l(w) Padded decompositions (FRT 04): can find a list of clusterings such that one cluster in each contains w(t) for all significant t in c* with high probability Moreover, if (Tlog(1/ )maxt c* Cov(y|t)-Cov(y|c*) / ) then we obtain a new cluster center in our list such that -w* R/2 So: we can iterate, reducing R 1/poly( m/ T) m large (t)-w* 0 with high probability
Finishing up: obtaining a k-DNF from Cast as weighted partial set cover instance (terms = sets of points) using i:t(x(i))=1li(w) as weight of term t and the ratio objective (cost/size) ZMJ 17: with ratio objective, still obtain O(log m) approximation Recall: we chose to optimize t c i:t(x(i))=1li(w) (=cost of cover c in set cover) adds only T-factor Recall: we only consider terms satisfied with probability /T use at most T/ terms Haussler 88, again: only need O(Tk/ log n) points
Summary: guarantee for general conditional linear regression Theorem. Suppose that D is a distribution over x {0,1}n, y Rd, and z R such that for some T-term k-DNF c* and w* Rd, <w*,y>-z is -subgaussian on D|c* with E[(<w*,y>-z)2|c*(x)] , Pr[c*(x)] , and E[(<w,y>-z)2|c*(x)] is -strongly convex in w with (Tlog(1/ )maxt c* Cov(y|t)-Cov(y|c*) / ) . There is a polynomial-time algorithm that uses examples from D to find w and c s.t. w.p. 1- , E[(<w,y>-z)2|c(x)] ( T (log log n + log )) and Pr[c(x)] (1- ) .
Comparison to sparse conditional linear regression on benchmarks Space_GA (m=3107, d=6) Cpusmall (m=8192, d=12) Small benchmarks (Bodyfat, m=252, d=14; Boston, m=506, d=13): does not converge https://github.com/wumming/lud
Outline 1. Introduction and motivation 2. Overview of sparse regression via list- learning 3. General regression via list-learning 4. Recap and challenges for future work
Summary: new algorithms for conditional linear regression We can solve conditional linear regression for k-DNF conditions on n Boolean attributes, regression on d real attributes when w is sparse: ( w 0 s for constant s) for all lp norms, loss ( nk/2) for general k-DNF loss ( T log log n) for T-term k-DNF For general coefficients w with -subgaussian residuals, maxterms t of c Cov(y|t) - Cov(y|c) op sufficiently small l2 loss ( T (log log n + log )) for T-term k-DNF Technique: list regression (BBV 08, J 17, CSV 17)
Open problems 1. Remove covariance requirement! 2. Improve large-formula error bounds to O(nk/2 ) for general (dense) regression 3. Algorithms without semidefinite programming? Without padded decompositions? Note: algorithms for sparse regression already satisfy 1 3. 4. Formal evidence for hardness of polynomial- factor approximations for agnostic learning? 5. Conditional supervised learning for other hypothesis classes?
References Hainline, Juba, Le, Woodruff. Conditional sparse lp-norm regression with optimal probability. In AISTATS, PMLR 89:1042-1050, 2019. Calderon, Juba, Li, Li, Ruan. Conditional Linear Regression. arXiv:1806.02326 [cs.LG], 2018. Juba. Conditional sparse linear regression. In ITCS, 2017. Rosenfeld, Graham, Hamoudi, Butawan, Eneh, Kahn, Miah, Niranjan, Lovat. MIAT: A novel attribute selection approach to better predict upper gastrointestinal cancer. In DSAA, pp.1 7, 2015. Balcan, Blum, Vempala. A discriminative framework for clustering via similarity functions. In STOC pp.671 680, 2008. Charikar, Steinhardt, Valiant. Learning from untrusted data. In STOC, pp.47 60, 2017. Fakcharoenphol, Rao, Talwar. A tight bound on approximating arbitrary metrics by tree metrics. JCSS 69(3):485-497, 2004. Zhang, Mathew, Juba. An improved algorithm for learning to perform exception- tolerant abduction. In AAAI, pp.1257 1265, 2017. Juba, Li, Miller. Learning abduction under partial observability. In AAAI, pp.1888 1896, 2018. Cohen, Peng. lp row sampling by Lewis weights. In STOC, pp.47 60, 2017. Haussler. Quantifying inductive bias: AI learning algorithms and Valiant s learning framework. Artificial Intelligence, 36:177 221, 1988. Peleg. Approximation algorithms for the label covermax and red-blue set cover problems. J. Discrete Algorithms, 5:55 64, 2007.
