Predicting Quality of Wine Using Linear Regression Analysis
Linear regression is a powerful method to analyze data and make predictions in the context of wine quality, particularly focusing on Bordeaux wines. This approach involves modeling the age of the wine, weather-related factors, and other independent variables to approximate quality and predict price trends accurately. Princeton Professor Orley Ashenfelter's use of linear regression to predict Bordeaux wine quality without tasting it has garnered attention, showcasing the effectiveness of this technique in the wine industry.
Uploaded on Sep 15, 2024 | 0 Views
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
CSCI 200 DATA MINING Introduction to Linear Regression Predicting Quality of Wine
Predicting Quality of Wine Linear Regression is simple and powerful method to analyze data and make predictions Bordeaux is a region in France popular for producing wine There are differences in price and quality from year to year that are sometimes very significant Bordeaux wines are widely believed to taste better when they are older. There is an incentive to store young wines until they are mature
Predicting Quality of Wine The main issue: it is hard to determine the quality of the wine when it is so young just by tasting it, since the taste will change significantly by the time it will be consumed Wine testers and experts taste the wine and then predict which ones will be the best one latest Question: can we model this process and make stronger predictions
Predicting Quality of Wine On March 4, 1990, the New York Times announced that Princeton Professor of Economics Orley Ashenfelter can predict the quality of Bordeaux wine without tasting a single drop. Ashenfelter's predictions have nothing to do with assessing the aroma of the wine. They are the results of a mathematical model. Ashenfelter used a method called linear regression.
Linear Regression The methods predicts an outcome variable or dependent variable. It uses a set independent variables. Dependent variable: a typical price in 1990-1991 for Bordeaux wine in an auction. This approximates quality. independent variables: age of the wine-- so the older wines are more expensive--and weather- related information
Linear Regression Four independent variables: The age of the wine The average growing season temperature The harvest rain The winter rain
Quality of Wine Linear Regression Professor Ashenfelter believed that his predictions are more accurate than those of the world's most influential wine critic, Robert Parker. Robert M. Parker Jr., generally regarded as the most influential wine critic in America, calls Professor Ashenfelter's research ''ludicrous and absurd.''
Predicting Quality of Wine - Links http://www.wine- economics.org/workingpapers/AAWE_WP0 4.pdf http://www.wine-economics.org/ http://www.nytimes.com/1990/03/04/us/win e-equation-puts-some-noses-out-of- joint.html
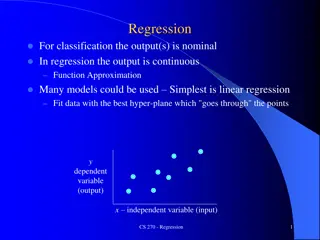
One-Variable Linear Regression This method uses one independent variable to predict the dependent variable Independent variable: average growing season temperature (AGST) The dependent variable, wine price. The goal of linear regression is to create a predictive line through the data. There are many different lines that could be drawn to predict wine price using average growing season temperature
Simple Prediction -Average The equation for this line: y = 7.07 This linear regression model would predict 7.07 regardless of the temperature.
Better Prediction 0.5*Only(AGST)-1.25 This linear regression model would predict a higher price when the temperature is higher.
General Equation Y = A*X + B the model X independent variable (in our case AGST) Y- dependent variable (in our case Price) Using this equation we will calculate PREDICTION values Model makes Errors Y=A*X+B+E Error term, E, is also often called a residual.
Y[i]=A*X[i]+B + E[i] For each observation, i, we have data for the dependent variable Yi and data for the independent variable, Xi. Using this equation we make a prediction. This prediction is hopefully close to the true outcome, Yi. Since the coefficients have to be the same for all data points, i, we often make a small error, E[i] The best model (choice of A and B) has the smallest error
SSE Sum of Squared Errors SSE for Average Line 10.15064 SSE for 0.5*AGST-1.25 6.03251
Better Measures for Regression Quality Root Means Squared Error (RMSE): RMSE = SQRT(SSE/N) (N is the total number of data points) R squared R2 R2 compares the best model to a baseline model Baseline model is the model that does not use any variables - AVERAGE The baseline model predicts the average value of the dependent variable regardless of the value of the independent variable.
R2 The sum of squared errors for the baseline model is also known as the total sum of squares, commonly referred to as SST. In our Example: SST= 10.15 R2 = 1 SSE/ SST SSE>=0, SST>=0 SSE<=SST (Y = A*X + B, if A = 0 we get Baseline Model) Linear regression model will never be worse than the baseline model. R2 = 1 Perfect Predictive Mode R2 = 0 No Improvement over the baseline
R2 R2is unitless and universally interpretable between problems. However, it can still be hard to compare between problems. Good models for easy problems will have an R2 close to 1. But good models for hard problems can still have an R2close to zero.
Regression Model Result The line that gives the minimum sum of squared errors is the line that regression model will find. Formula for the Linear Regression Model: Y = 0.63509*AGST-3.4178 R2 = 0.43502 SSE = 5.73488
