Understanding Euclid's Geometry: The Fundamentals Explained
Euclid, known as the Father of Geometry, introduced the principles of geometry in Egypt. His work included definitions, axioms, and postulates that laid the foundation for geometric reasoning. Euclid's Five Postulates are crucial in understanding the basic concepts of geometry. This article provides insights into Euclid's contributions to the field of mathematics.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
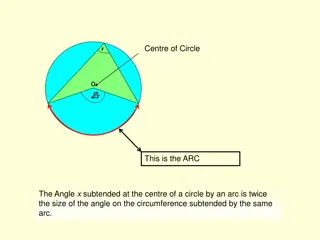
EUCLIDS GEOMETRY GEOMETRY GEO METREIN Earth Tomeasure Geometry originated in Egypt as an art of Earthmeasurement Euclid (325 BCE-265 BCE): The Father of Geometry The first Egyptian mathematician who initiated a new way of thinking the study of geometry. Introduced the method of proving a geometrical result by deductive reasoning based upon previously proved result & some self evident specific assumptions called axioms.
Euclids Definitions Euclid has listed 23 definitions in Book-1 of the Elements ; a few are : A point is that which has no part. A line is breadth less length. The ends of a line are points. A straight line is a line which lies evenly with the points on itself. A surface is that which has length & breadth only. The edges of a surface are lines. A plane surface is a surface which lies evenly with the straight lines on itself.
Euclids Axioms & Postulates Euclid assumed certain properties which are actually obvious universal truths & divided them into twotypes: Postulates the assumptions specific togeometry. Axioms - the assumptions used throughoutmathematics & not specifically linked to geometry.
Euclids Axioms Things which are equal to the same thing are equal to one another. i.e. If A = C & B = C, then A = B. Here A, B & C are same kind of things. If equals are added to equals, the whole are equal i.e. If A = B & C = D, then A + C = B + D Also A = B then this implies that A + C = B + C. If equals are subtracted from equals, the remainders are equal. Things which coinside with one another are equal to one another.
The whole is greater than the part. i.e. If A > B then there exists C such that A = B + C. Here B is a part of A & therefore A is greater than B. Things which are double of the same things are equal to one another. The things are halves of the same things are equal to one another.
Euclids Five Postulates Postulate 1: A straight line may be drawn from any one point to any other point. Axiom: given two distinct points, there is a unique line that passes throughthem. Postulate 2: A terminated line can be producedindefinitely. Postulate 3: A circle can be drawn with any centre and any radius. Postulate 4: All right angles are equal to one another.
Postulate 5: If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two rightangles.
EuclidsTheorems Theorems- provedstatements, 465 theorems in a logical chain using his axioms, postulates & definitions. Theorem 1: Two distinct lines cannot have more than one point in common.
Equivalent version of Euclids fifth postulate There are several equivalent versions of fifth postulate; one of them is Playfair s axiom (a Scottish mathematician in 1729) as statedbelow: For every line l and for every point p not lying on l, there exists a unique line m passing through p & parallel to l.
Conclusion Euclid did not require his fifth postulate to prove his first 28 theorems but he himself including many mathematicians were convinced that the fifth postulate is actually a theorem that can be proved using just the four postulates and other axioms. However all attempts to prove the fifth postulate as a theorem have failed & this led to a great achievement the creation of several other geometries , quite different from Euclidean geometries called as non- Euclidean geometries. Example, Spherical geometry, the geometry of the universe we live in.