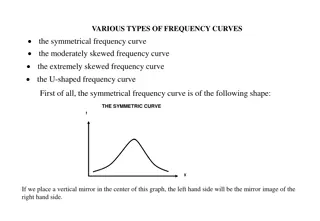
Understanding B-Spline Curves in Computer Graphics
Exploring the advantages of B-spline curves over Bezier curves, this content delves into the representation, calculation of basis functions, and properties of B-spline curves. The discussion includes issues with Bezier curve representation, local control in B-spline curves, and the subdivision of the domain by knots. The content also covers B-spline basis functions, observations related to basis functions, and the influence of basis function coefficients.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
CS552: Computer Graphics Lecture 21: B Spline Curve
Recap Bezier curve o Properties o Rendering o De Casteljau's Algorithm o Subdividing Bezier Curve o Continuity of curve ?0 ?1 ?2
Objective After completing this lecture, students will be able to o Explain the issues with Bezier curve representation o Explain the advantage of B spline curve o Calculate the B-spline basis of different degrees and knot intervals
Bezier Curves: Issues No local control Degree of curve is fixed by the number of control points
B Spline Each control point has a unique basis function Local control is facilitated
B spline Curves The user supplies: the degree p, n+1 control points, and m+1 knot vectors Write the curve as: n ( ) t ( ) t = i = p P P N i i 0 The functions Nipare the B-Spline basis functions B-Spline Animation B-Spline Animation
B Spline Basis The domain is subdivided by knots, and Basis functions are not non-zero on the entire interval. Some knot spans may not exist (Repeat) o Simple / Multiple Knots o Uniform/ Non-Uniform Knots The i-th B-spline basis function of degree p 0? = 1,?? ? ??+1 ?? ?????? ?? B-Spline Basis Plots B-Spline Basis Plots ? 1? +??+?+1 ? ??+?+1 ?? ? ?? ??+? ?? ?? = ? 1? ?? ?? ??+1 Cox-de Boor recursion formula
B Spline Basis: Observations 1 Non-zero domain of a basis function Basis function ??,?(?) is non-zero on [??,??+?+?)
B Spline Basis: Observations 2 Influence of the basis function coefficients ? ??+? ??+?+1 ?? ??+1 ??+? ?? ? ?? ??+?+1 ? ??+?+1 ??+1 Linear combination of two intervals, where both are linear in ?
Example Suppose the knot vector is U = { 0, 0.25, 0.5, 0.75, 1 }. Hence, m = 4 and u0= 0, u1= 0.25, u2= 0.5, u3= 0.75 and u4= 1. Degree Basis Function Range Equation 0 ?0 0 ?1 ?2 ?3 ?0 ?1 ?2 0 0 0 1 1 1 1
Thank you Next Lecture: B-Spline Curve