Ginzburg Landau phenomenological Theory
The Ginzburg-Landau phenomenological theory explains superconductivity and superfluidity as distinct thermodynamic phases. It focuses on phase transitions characterized by singularities in specific heat at the transition temperature. Derived from BCS theory, it quantifies condensation energy, emphas
3 views • 38 slides
Lenticulars adhesive label, Lenticular security labels, Custom lenticular stickers Manufacturer from Kolkata India
Understanding the diverse needs of the clients,we have come up with an excellent range of Lenticular Label. Our offered range is a piece of ribbed plastic, ranging from 15 line per inch to 150 line per inch. Each rib is a lens and each lens is set up according to viewing distance, depth and field to
0 views • 3 slides
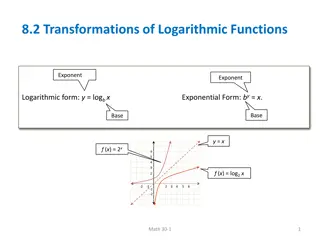
Logarithmic Function Transformations
Explore transformations of logarithmic functions through examples involving vertical and horizontal stretches, translations, and reflections. Understand how to sketch the graphs of logarithmic functions and determine missing coordinates on the graphs. Additionally, learn about transformations such a
3 views • 9 slides
Logarithmic Functions with Examples
Explore logarithmic functions based on the book "Functions, Data, and Models" by S.P. Gordon and F.S. Gordon. Learn about population growth modeling, logarithm definitions, fundamental identities, and solving equations using logarithms. Examples include determining population growth, solving for var
1 views • 17 slides
Review of Definite Integrals using the Residue Theorem
Singular integrals involving logarithmic and non-integrable singularities are discussed, emphasizing integrability in the principal value sense. Cauchy Principal Value integrals and examples of their evaluations for singularities like 1/x are explored, highlighting the necessity of passing through t
1 views • 48 slides
Laws of Logarithms: Exponents vs. Logarithms
Laws of Logarithms explain the properties and rules governing logarithmic functions, involving evaluations, conversions, additions, subtractions, and comparisons with exponent laws. Through examples, the laws of logarithms are applied to simplify expressions and evaluate logarithmic equations. The r
0 views • 17 slides
Logarithmic Functions and Their Inverses
Mathematically exploring logarithmic functions, their properties, inverse functions, exponential forms, and rewriting logarithmic expressions. Learn how to evaluate logarithms through examples and understand the relationship between exponential and logarithmic forms.
1 views • 24 slides
The Residue Theorem in Complex Analysis
The Residue Theorem is a powerful tool in complex analysis that allows us to evaluate line integrals around paths enclosing isolated singularities. By expanding the function in a Laurent series, deforming the contour, and summing residues, we can evaluate these integrals efficiently. This theorem ex
2 views • 31 slides
Logarithms and Logarithmic Laws
Logarithms help us determine the power to which a base must be raised to give a specific result. This content explains concepts like logarithmic laws, changing bases, solving logarithmic equations, and includes examples for better understanding.
0 views • 8 slides
Indian Contributions to General Relativity Post-Independence Era
Indian scholars have made significant contributions to the field of General Relativity post-independence, focusing on important problems like Big Bang singularity, gravitational collapse, black holes, gravitational waves, and quantum aspects. Notable achievements include AKR's Raychaudhury Equation,
0 views • 30 slides
Convex Optimization: Interior Point Methods Formulation
This chapter on interior point methods in convex optimization explores the formulation of inequality-constrained optimization problems using barrier methods and generalized inequalities. It covers primal-dual interior point methods and discusses issues such as exponential complexity and determining
0 views • 24 slides
Mathematics and Economics in Social Sciences
Explore the intersection of mathematics and economics in social and behavioral sciences through examples in algebra, precalculus, and real analysis. Solve problems related to demand functions, supply curves, subsidies, and taxes. Understand the impact of programs like WIC on family budgets. Discover
1 views • 20 slides
Regression Transformations for Normality and Simplification of Relationships in U.S. Coal Mine Production 2011
The study analyzes Coal Mine Production data from 2011, focusing on predictor variables like Labor Effort, Surface Mine status, and regional factors. An initial regression model with interactions is presented, but residual plots indicate the need for transformation. The Box-Cox transformation is emp
1 views • 13 slides
Earthquake Magnitudes and Seismic Measurements
Delve into the fundamentals of engineering seismology and earthquake magnitudes, exploring topics such as fault dimensions, slip distribution, spectral shapes, Richter's observations, and logarithmic scales. Gain insights into how seismic measurements are characterized and understand the significanc
1 views • 69 slides
Wind Profiles and Aerodynamic Roughness Length
Wind profiles are crucial in understanding how wind speed changes with height in the boundary layer. The logarithmic and power law profiles depict this relationship, influenced by surface characteristics and obstacles. The aerodynamic roughness length, defining where wind speed becomes zero, remains
0 views • 14 slides
Philosophical Implications of General Relativity: Black Holes, Cosmology, and More
Delve into the profound implications of General Relativity on topics such as black holes, cosmology, and philosophical consequences from Special and General Relativity. Discover how curved geometry allows for different topologies, potential return of preferred frames, the concept of horizons near bl
1 views • 18 slides
Finite-time Analysis of the Multiarmed Bandit Problem in Advanced Algorithms Seminar
This study delves into the Stochastic Multiarmed Bandit Problem and explores achieving logarithmic regret uniformly over time. It covers problem settings, notations, previous work, objectives, results, and proofs, including the usage of the UCB1 policy. The theorem and its proof demonstrate the expe
1 views • 43 slides
Mastering Graph Axes Customization: Techniques and Tricks
Explore advanced techniques for customizing graph axes by adjusting scales, labels, and ticks. Learn how to suppress ticks, modify label alignment, and work with non-standard scales like logarithmic or reciprocal. Discover ways to maintain consistent styles across a series of graphs and gain more co
0 views • 57 slides
Revisiting Adjustor Curves for Total Phosphorus Removal Rates
Based on a literature review, it was found that a 5th-order polynomial curve is a better fit than the originally used logarithmic trendline for anchor rates of percent Total Phosphorus removal related to runoff depth. The expert panel report reflects the old curves while trendline equations in FAQ d
0 views • 7 slides
Singularities in Complex Analysis: Notes and Examples
Singularities are points where a function is not analytic. Through Taylor and Laurent Series, we explore the behavior of functions near singularities, their convergence, and divergence properties. Taylor Series Examples demonstrate poles and divergent behaviors, while Laurent Series Examples illustr
1 views • 23 slides
ICE Price Analysis for ERCOT Credit Risk Exposure
CWG/MCWG is exploring the use of ICE futures prices to assess ERCOT's credit risk exposure. This involves analyzing the relationship between ICE prices and actual RTM prices. The data inputs and transformations include calculations of daily average prices, logarithmic adjustments for linear regressi
0 views • 22 slides
Nonstationary Configurations of a Spherically Symmetric Scalar Field
Action and stress-energy tensor, Einstein-Klein-Gordon equations, and method for constructing nonstationary configurations of a spherically symmetric scalar field are discussed in this study. The behavior of the characteristic function allows interpretations such as black holes, wormholes, or naked
1 views • 14 slides
Improved Truthful Mechanisms for Subadditive Combinatorial Auctions
This research paper discusses strategies to maximize welfare in combinatorial auctions. It explores mechanisms for handling strategic bidders with private valuations, aiming to design truthful and optimal welfare mechanisms while considering polytime constraints. The study presents advancements in a
0 views • 19 slides
Methods of Integration and Trigonometric Substitution
Explore methods of integration including integration by parts and trigonometric substitution. Learn how to apply these techniques to solve integrals involving logarithmic, trigonometric, and rational functions. Discover step-by-step processes and identities to simplify and evaluate various types of
1 views • 7 slides
Quasi-Interpolation for Scattered Data in High Dimensions: Methods and Applications
This research explores the use of quasi-interpolation techniques to approximate functions from scattered data points in high dimensions. It discusses the interpretation of Moving Least Squares (MLS) for direct pointwise approximation of differential operators, handling singularities, and improving a
1 views • 9 slides
Advanced Techniques in Multivariate Approximation for Improved Function Approximation
Explore characteristics and properties of good approximation operators, such as quasi-interpolation and Moving Least-Squares (MLS), for approximating functions with singularities and near boundaries. Learn about direct approximation of local functionals and high-order approximation methods for non-s
0 views • 9 slides
Derivative of Logarithmic Functions
Learn how to find derivatives of logarithmic functions using natural logarithms, important techniques for challenging derivatives involving functions raised to functions, sine, product, quotient, and chain rule problems. Follow steps in logarithmic differentiation to simplify calculations and solve
0 views • 5 slides
AVL Trees in Data Structures
AVL trees are self-balancing binary search trees that help maintain efficiency in operations by ensuring the tree remains balanced. By enforcing a balance condition, AVL trees aim to keep the depth of the tree logarithmic, leading to O(log n) complexity for operations such as find, insert, and delet
0 views • 39 slides
AVL Trees: Balanced Search Trees for Efficient Operations
AVL Trees are balanced search trees that ensure efficient insertion, deletion, and retrieval operations with a worst-case time complexity of O(log N). Named after their inventors Adelson-Velskii and Landis, AVL Trees maintain balance by limiting the height difference between left and right subtrees
0 views • 28 slides
Logarithms: Laws, Examples, and Applications
Logarithms are important mathematical tools used in various calculations. This content covers the basics of logarithms, logarithmic laws, solving logarithmic equations, and practical examples. Explore the concept of logarithms and their applications in different scenarios.
0 views • 8 slides
Logarithms: Properties, Expansion, Condensation, and Evaluation
Explore the properties of logarithms including expansion, condensation, and evaluation. Learn how to expand and condense logarithmic expressions, evaluate logarithms using different bases, and convert logs into other bases. Practice changing the base to evaluate logarithmic equations.
0 views • 5 slides
Developing Pure Julia Codes for Elementary Functions in MIT's 18.337 Course
Mustafa Mohamad from MIT's Department of Mechanical Engineering teaches the Fall 2016 course on developing pure Julia codes for elementary functions. The focus is on functions like Trigonometric (sin, cos, tan, etc.), Hyperbolic (sinh, cosh, tanh, etc.), Exponential and Logarithmic, and Floating-Poi
0 views • 19 slides
Quantum Space-Bounded Complexity in Logarithmic Space: A Comprehensive Overview
Quantum space-bounded complexity explores the memory requirements for solving problems in log space. Examples include matrix multiplication, undirected graph connectivity, and problems like inverting matrices and determining connectivity. The significance of deterministic log space (NL) and nondeter
0 views • 49 slides
Observational Phenomena in Axially Symmetric Spacetimes with Non-Negative Cosmological Constant
This study delves into observational phenomena in spacetimes with non-negative cosmological constants, focusing on photon motion, Kerr-de Sitter geometries, and shadows of Kerr-de Sitter naked singularities. Explore related concepts such as spherical photon orbits, measuring NS spin, and equations o
0 views • 18 slides
Snapshot-Oblivious RAMs: Sub-Logarithmic Efficiency for Short Transcripts
Innovative research on Snapshot-Oblivious RAMs reveals sub-logarithmic efficiency for short transcripts, addressing database breach risks through bypassing inherent lower bounds with a focus on enhancing memory access security.
0 views • 53 slides
Logarithmic Functions and Exponential Equations
In this unit, learn how to write and evaluate logarithmic expressions, solve exponential equations using common bases, work with exponential and logarithm equations, understand logarithmic form, and find the inverse of functions. Practice solving equations with various bases and learn to convert bet
0 views • 7 slides
Two-Stage Op-Amp Design for GBW and Phase Margin
Singularities in the small-signal equivalent circuit are analyzed for the two-stage op-amp design aiming for a specific GBW and phase margin. The preliminary assumptions involve canceling a zero and approximating the frequency response with dominant poles. Specifications for stability, unity-gain an
0 views • 24 slides
Exponential and Logarithmic Equations Exploration
Discover the principles of solving exponential and logarithmic equations with examples and step-by-step guides. Learn how to manipulate expressions on both sides to find the variable. Utilize logarithms to simplify exponential equations effectively.
0 views • 10 slides
Understanding Robot Motion Through Differential Kinematics
Delve into the world of robot motion by exploring the Differential Kinematics method, which involves analyzing pose velocities of frames using differential forms of homogeneous transformations. This chapter compares this approach to conventional dynamics vector methods and discusses the crucial role
0 views • 37 slides
Understanding Pulp Suspension Flows and Head Loss Profiles
Explore the characterization of pulp suspension flows at low concentrations, head loss in pipes, and singularities for better insights. Discover test rigs, equipment, and behavior of fiber suspensions using advanced techniques like Pulsed Ultrasonic Doppler Velocimetry.
0 views • 22 slides